この記事は、インテル® ソフトウェア・ネットワークに掲載されている「Using Intel® Advanced Vector Extensions to Implement an Inverse Discrete Cosine Transform」(https://software.intel.com/sites/default/files/m/d/4/1/d/8/UsingIntelAVXToImplementIDCT-r1_5.pdf) の日本語参考訳です。
ソースコードのダウンロード: http://software.intel.com/file/29048
はじめに
変換アルゴリズムのコーディングは、イメージ/ビデオ処理アプリケーションの重要なステップです。イメージのピクセルには、近隣ピクセルとの相関性情報が含まれており、連続するフレームの隣接ピクセルは非常に高い相関性を示します。これらの相関性は隣接ピクセルの値の予測に使用できます。相関性の高い空間データは周波数領域の相関しない係数に変換されます。変換されたデータ (係数として表現) は独立しており、個別に操作できます。人間の視覚は、高周波数の変化よりも低周波数の変化に敏感です。このため、エンコーダーは、高周波数の係数をゼロに設定した後で圧縮を行います。逆変換はデコーダー・パイプラインで使用され、ソースデータを再構築します。
図 1 および図 2 は、典型的なイメージ・エンコーダー・システムとイメージ・デコーダー・システムのコンポーネントを示しています。


離散コサイン変換 (DCT) と逆離散コサイン変換 (IDCT) は、MPEG、JPEG、その他のイメージ処理システムのエンコーダー・パイプラインとデコーダー・パイプラインで幅広く使用されています。優れたユーザー体験を提供するには高速で正確な IDCT 変換が重要です。
インテル® アドバンスド・ベクトル・エクステンション (インテル® AVX) は、新しいインテル® マイクロアーキテクチャー (Sandy Bridge) で導入された機能で、浮動小数点データや逆離散コサイン変換などの演算に対して、インテル® ストリーミング SIMD 拡張命令 (インテル® SSE) の機能が拡張されています。インテル® AVX では現在の XMM レジスターの幅が実質的に 2 倍になり、より広いデータ幅を処理できる新しい拡張機能が追加されています。また、インテル® AVX は、以前の 128 ビット SIMD 命令セットの拡張よりも電力効率が改善され、浮動小数点処理のパフォーマンスが大幅に向上しています。
ここでは、インテル® AVX と新しいインテル® マイクロアーキテクチャー (Sandy Bridge) のさまざまな機能 (よりワイドな 256 ビットの SIMD レジスター、非破壊的なソースオペランド、新しいデータ操作と演算プリミティブ、2 つの 128 ビット・ロード・ポート、計算実行幅の倍増など) が逆離散コサイン変換 (IDCT) 処理にどのように役立つかについて説明します。インテル® AVX は、精度の影響を受けやすいハイパフォーマンス浮動小数点変換アプリケーションの演算スループットを向上させます。整数実装も、非破壊的ソースオペランドのような機能による恩恵を受けます。
インテルでは、インテル® AVX 対応のインテル® C++ コンパイラー、インテル® ソフトウェア・デベロップメント・エミュレーター (SDE)、インテル® アーキテクチャー・コード・アナライザーなどのインテル® AVX ソフトウェア開発ツールも提供しています。これらのツールはすべて、このカーネルの開発中に効率的に使用されました。ツールは、インテル® AVX Web サイト (http://software.intel.com/en-us/avx/) からダウンロードできます。
テスト環境
ここに記述されているパフォーマンスは、新しいインテル®マイクロアーキテクチャー (Sandy Bridge) ベースの量産前試作 CPU 上で実行した値を測定したものです。また、IDCT アルゴリズムの演算を開始する前にプロセッサーの 1 次キャッシュにテストデータがロードされていると仮定しています。パフォーマンスの比較は、C 組み込み関数を使用してインテル® AVX と対応するインテル® SSE 実装を実行したときの相対的なパフォーマンスに基づいて行われています。コードのコンパイルには、64 ビット版のインテル® C++ コンパイラー 11.1.038 を使用し、以下のコマンドライン・オプションを使用しました。
- インテル® SSE: /QxSSE4.1 /O3
- インテル® AVX: /QxAVX /O3
短整数 (short integer) のパフォーマンスの比較は、異なる命令セット・アーキテクチャー向けにインテル® SSE 実装をコンパイルして行われました。/QxAVX オプションを指定すると、コンパイラーは VEX エンコード・フォーマットのインテル® SSE 命令を生成します。/QxSSE4.1 オプションを指定すると、コンパイラーはインテル® SSE 4.1 命令を生成します。非破壊的ソースオペランドは VEX エンコード・フォーマットの命令で導入されたものです。
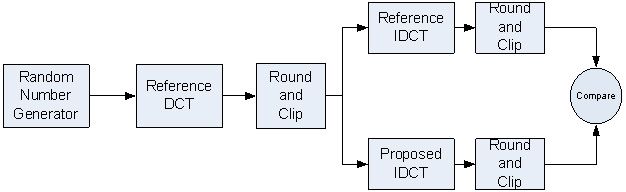
テスト・アプリケーションは、IEEE 標準規格 1180-1900 (参考文献 5) のセクション 3 の 8×8 IDCT 精度要件に従っています。ランダムに生成された入力データがリファレンス DCT で処理されます。DCT の出力は最も近い整数に丸められます (-2048 <= value < 2047)。この丸められた値がリファレンス IDCT と (テストする) IDCT の入力になります。IDCT の出力は最も近い整数に丸められます (-256 <= output < 255)。2 つの結果が比較され、精度測定が行われます。
このアプリケーションでは、オリジナルコードは倍精度浮動小数点スカラー C コードを使用して実装されています。テストした IDCT 実装は、インテル® SSE 短整数バージョン、インテル® SSE 単精度浮動小数点バージョン、およびインテル® AVX 単精度浮動小数点バージョンです。ベクトルバージョンはすべて C の組み込み関数で実装されています。
離散コサイン変換
離散コサイン変換 (DCT) は、イメージの空間データを周波数領域に変換します。数学的な演算は、参考文献 [1] で詳細に説明されています。
2 次元 (2D) DCT は 64 (8×8 ブロック) のピクセル値を 64 の係数に変換します。イメージのピクセル値は、余弦基底関数の振幅から導き出された係数に変換されます。
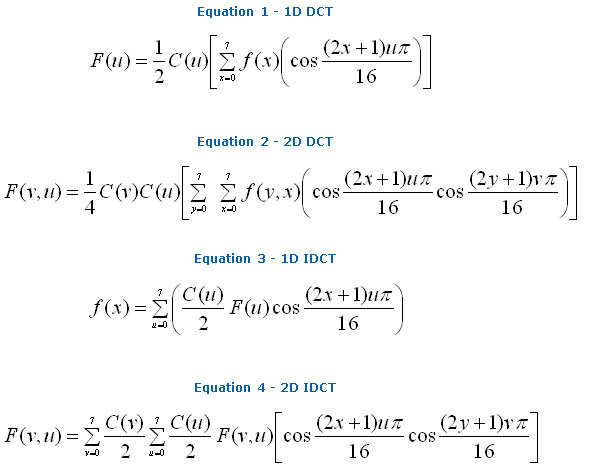
意味:

参考文献 [2] は、数学的な演算の数を要約したものです。DCT 方程式と IDCT 方程式を比較すると、変換には同じ数の演算が必要であることが分かります。Equation 2 は、2D DCT では係数ごとに 64 の乗算と 63 の加算が必要であることを示しています。このため、8×8 ブロックを変換するには、4096 の乗算と 4032 の加算が必要になります。
2D DCT を 8 行の 8 つの 1D DCT と 8 列の 8 つの 1D DCT に置換すると、演算数を減らすことができます。Equation 1 は、1D DCT では 8 つの係数を生成するために 64 の乗算と 56 の加算が必要であることを示しています。このため、1D DCT で 8×8 ブロックを変換するには、1024 の乗算と 896 の加算が必要になります。参考文献 [1] および [4] では、その他の DCT および IDCT アルゴリズムを説明しています。
先行研究と仕様
以下の先行研究と仕様を背景情報として確認してください。
- 参考文献 [1] では、JPEG の仕様を説明しています。
- この記事のインテル® AVX 実装で使用されている IDCT アルゴリズムは、参考文献 [2] で説明されている最適化アルゴリズムに従っています。
- 参考文献 [3] には、追加の背景情報が含まれています。
IDCT のインテル® AVX 実装
先行研究で説明されているように、この記事のアルゴリズムは 8×8 ブロックの行で 8 つの 1D IDCT 変換を行います。次に、これらの結果の列で 8 つの 1D IDCT を行います。2 つの異なる 1D IDCT 変換が使用され、どちらの変換にも転置は必要ありません。
インテル® AVX 実装では、データの 2 つの行を同時に演算します。まず、各行の 4 つの float を個別の 128 ビット・レジスターにロードします。128 ビットのロードを行う理由はすぐに分かります。128 ビット XMM レジスターが、対応する 256 ビット YMM レジスターの下位 128 ビットとオーバーレイすることに注意してください。YMM レジスターの上位 128 ビットには、_mm256_insertf128_ps 命令により、これらの行に含まれる 4 つの float の次のセットがロードされます。
その結果、YMM レジスターには、下位 128 ビットのある行に含まれる 4 つの float の最初のセットと、上位 128 ビットの 2 つ目の行に含まれる 4 つの float の 2 つ目のセットが含まれます。8 つの float をロードするには多くの処理が必要になるのに、なぜこの方法を使用するのでしょうか。この方法は、(次のロードが現在のメモリー位置から 1 ストライド以上離れたメモリー位置から読み取られるため) ストライドロードと呼ばれます。
ストライドロードは特定のアプリケーションで効率的です。
- IDCT では 8 つの積和を求める必要がありますが、積が 2 つの YMM レジスターの同じレーンに含まれる場合、積和を求めるのは簡単です。2 つのレジスターには、両方のレジスターの下位 128 ビットのある行に含まれる内容と、両方のレジスターの上位 128 ビットの 2 つ目の行に含まれる内容がロードされます。図 4 から図 6 を参照してください。
- ストライドロードを使用する別の利点は、データの移動がシャッフルポートとは異なる実行ポートで行われる (128 ビットのメモリーオペランドが上位 128 ビットに配置される) ことです。シャッフルを行うポートの使用が減り、実行ポートに作業がより均等に割り当てられます。
- 2 つの行の float 4-7 を 1 つのレジスターにロードするもう 1 つの利点は、行の処理の終盤に発生するシャッフルが減少することです。
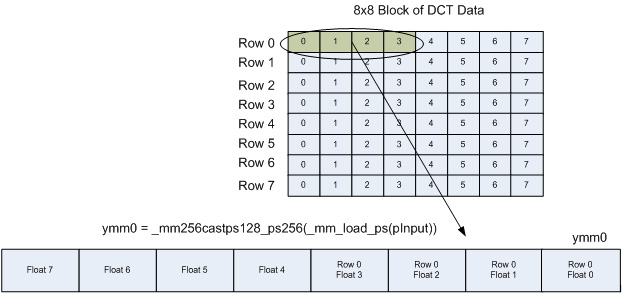
_mm_load_ps 命令と _mm256_castps128_ps256 命令を組み合わせて、128 ビットを YMM レジスターの最下位 128 ビットにロードします。
図 5 は、Row 4 のデータのストライドロードと、YMM0 レジスターの最上位 128 ビットへのロードを示しています。
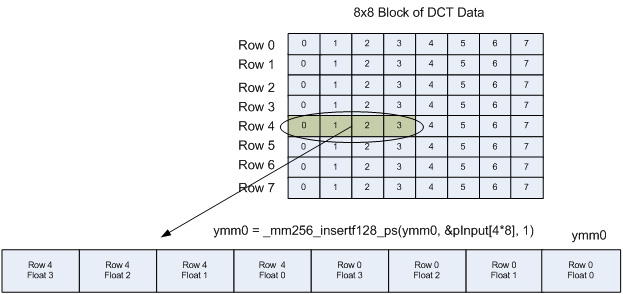
2 つ目の YMM レジスターにも同様の方法で両方の列に含まれる 4 つの float の 2 つ目のセット (float 4-7) がロードされます。結果を図 6 に示します。

入力データは複数の余弦項で乗算する必要があります。図 7 に示す乗算の準備のために、各行に含まれる 1 つの float を _mm256_shuffle_ps で処理します。ここでは、float 0 がコピーされています。
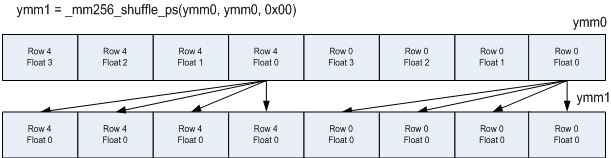
2 つの _mm256_mul_ps 命令は、必要な余弦の乗算を行います。この処理により、7 つの積和項目の 1 つが完了します。
この命令シーケンスを 3 回繰り返し、異なる入力値と余弦項の組み合わせで演算を行います。この時点では、4 つのレジスターに積和が含まれます。つまり、あるレジスターには float 0 と 2 の積和、別のレジスターには float 1 と 3 の積和、別のレジスターには float 4 と 6 の積和、最後のレジスターには float 5 と 7 の積和がそれぞれ含まれます。
積和を完了するには、あと 3 つの処理が必要です。すべての偶数項目の積和を追加し、すべての奇数項目の積和を追加します。これが残り 3 つの処理の 2 つです。
ymm_even = _mm256_add_ps(r_ymm02, r_ymm46);
ymm_odd = _mm256_add_ps(r_ymm13, r_ymm57);
最後の 7 つ目の処理では、出力の最下位の 4 つの float を計算します。最上位の 4 つの float を計算するには減算が必要ですが、float の順序は正しくありません。
ymm_diff = _mm256_sub_ps(ymm_even, ymm_odd);
ymm_sum = _mm256_add_ps(ymm_even, ymm_odd);
2 つの行の最上位の float の順序は、図 8 に示すように、_mm256_shuffle_ps 命令を使用して適切に調整することができます。各入力行の最上位の 4 つの float を配置する利点はより明白です。
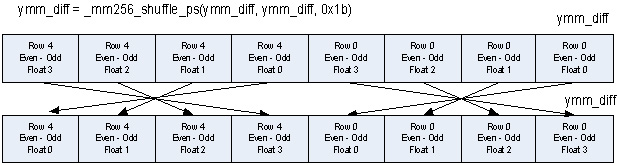
これらの 2 つの行の 1D IDCT の最終ステップは、各行の結果を 2 つの _mm256_ permute2f128 命令を使用して同じ 256 ビット・レジスターに再結合することです。
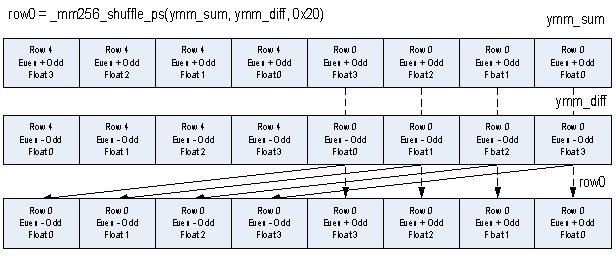

これで 2 セットの行の 1D IDCT は完了です。このシーケンスを行 1 と 7、2 と 6、そして最後に 3 と 5 に繰り返して、8 つの行の 1D IDCT を完了します。
8 つの行の 1D IDCT が完了したら、8 つの列の 1D IDCT を始めます。積和がすでに加算のための適切な位置に配置されているので、アルゴリズムはより単純です。列の 1D IDCT ではシャッフルは必要ありません。
列の浮動小数点 IDCT では 4 つの add 命令を省略できます。
//row5*tangent + row5
r_ymm0 = _mm256_mul_ps(row5, tangent);
r_ymm0 = _mm256_add_ps(row5, r_ymm0);
列と正接項目+1 の乗算を行うと、浮動小数点実装と同一の結果になります。
Tangent_p1 = tan(x) + 1
//row5*(tangent+1)
r_ymm0 = _mm256_mul_ps(row5, tangent_p1);
//row3*(tangent+1)
r_ymm1 = _mm256_mul_ps(row3, tangent_p1);
アルゴリズムのスケーリングに関する問題のため、この最適化は短整数実装には適用できません。
インテル® アーキテクチャー・コード・アナライザーの使用
インテル® アーキテクチャー・コード・アナライザーは、基本ブロックのクリティカル・パス、実行ポートの使用率、命令の使用率などの情報を表示する優れたツールです。インテル® アーキテクチャー・コード・アナライザーの詳細な情報は、インテル® AVX Web サイト (https://software.intel.com/en-us/avx/) を参照してください。
図 11 の基本ブロック解析は、vshufps (_mm256_shuffle_ps 組み込み関数により起動) がポート 5 で実行されていることを示しています。解析では、vinsertf128 命令 (_mm256_insertf128_ps 組み込み関数) がポートを選択して実行できることも示しています。インテル® アーキテクチャー・コード・アナライザーのレポートの “X” は、このアルゴリズムでは命令が別のポートで実行されたことを示しています。ここでは、2 つ目のソースオペランドがメモリーからロードされているため、vinsertf128 はポート 3 とポート 5 ではなく、ポート 0 とポート 3 で実行されています。挿入がポート 0 で行われることにより、ポート 5 の負荷が低下しています。

インテル® アーキテクチャー・コード・アナライザーは、アプリケーションを細かくチューニングしてパフォーマンスの向上を目指すソフトウェア開発者向けの効率的な最適化ツールです。
結果
128 ビットのコードは、以前のインテル® マイクロアーキテクチャー (Nehalem) 向けにコンパイルされたインテル® SSE コードを新しいインテル® マイクロアーキテクチャー (Sandy Bridge) ベースのシステムで実行したものです。対応する 256 ビットのコードは、新しいインテル® マイクロアーキテクチャー (Sandy Bridge) 向けにコンパイルされたインテル® AVX 対応のコードを、新しいインテル® マイクロアーキテクチャー (Sandy Bridge) ベースのシステムで実行したものです。
データは、インテル® SSE コードでは 16 ビット境界、インテル® AVX コードでは 32 ビット境界でそれぞれアライメントされています。アプリケーションのビルドには、64 ビット版のインテル® C++ コンパイラー 11.1.038 を使用しました。次の表のスピードアップは、256 ビット・コードと対応する 128 ビット・コードを比較した値を示しています。
表 1 – パフォーマンス結果
| アルゴリズム | スピードアップ | 比較対象 |
| インテル® AVX 浮動小数点実装 | 0.94 | インテル® SSE 短整数実装との比較 |
| インテル® SSE 短整数実装 (/QxAVX でコンパイル) | 1.07 | インテル® SSE 短整数実装 (/QxSSE4.1 でコンパイル) との比較 |
| インテル® AVX 浮動小数点実装 | 1.78 | インテル® SSE 浮動小数点実装との比較 |
表 2 は、各実装における全体的な平均誤差の結果を要約したものです。
表 2 – 全体的な平均誤差の結果
| L、H (参考文献 5) | インテル® SSE 短整数 | インテル® SSE 単精度浮動小数点 | インテル® AVX 単精度浮動小数点 |
| 256, 255 | 3.44e-5 | 6.25e-6 | 6.25e-6 |
| 5, 5 | 2.58e-4 | 1.56e-6 | 1.56e-6 |
| 300, 300 | 4.69e-6 | 6.25e-6 | 6.25e-6 |
| -255, 256 | 7.53e-4 | 3.13e-6 | 3.13e-6 |
| -5, 5 | 0 | 0 | 0 |
| -300, 300 | 0 | 0 | 0 |
| 入力 = 0 | 0 | 0 | 0 |
短整数実装と単精度浮動小数点実装はどちらも IEEE 標準規格 1180-1900 (参考文献 5) の誤差要件を満たしています。浮動小数点実装は多くのテストで全体的な平均誤差が低くなっています (短整数実装の 1/5、1/165、1/240)。
まとめ
10,000 8×8 ブロックの IDCT の結果は、インテル® AVX 実装がインテル® SSE 単精度浮動小数点実装よりも 1.78 倍高速であることを示しています。基準の IDCT と比較した場合の精度も非常に高くなっています。
結果は、インテル® SSE 短整数バージョンを /QxAVX オプションを指定してコンパイルすると、同じコードを /QxSSE4.1 オプションを指定してコンパイルした場合よりも 1.07 倍高速であることも示しています。/QxSSE4.1 オプションを指定してコンパイルするとアセンブリー言語で 22 のレジスター間移動命令が生成されますが、 /QxAVX オプションを指定してコンパイルするとレジスター間移動命令は生成されません。インテル® AVX の非破壊的ソース命令は、このアプリケーションにおけるレジスターコピーの必要性を軽減します。今日では、インテル® AVX ベースのアルゴリズムを使用するメリットは大いにあると言えます。
インテル® AVX 実装はインテル® SSE 短整数バージョンよりも少し遅くなりますが、インテル® AVX 単精度浮動小数点バージョンはより正確です。インテル® SSE 短整数バージョンの精度を向上させて丸め誤差を最小にするにはさまざまな調整が必要です。このような調整は浮動小数点実装では必要ないため、浮動小数点実装がより優れた実装であることは明白です。
IDCT のソースコード
IDCT のソースコードは http://software.intel.com/file/29048 からダウンロードできます。
ソースコードの一部を以下に示します。
void idctAVX(void) {
__m128 r_xmm0, r_xmm2, r_xmm1;
__m256 r_ymm02, r_ymm46, r_ymm13, r_ymm57;
__m256 r_ymm0, r_ymm1, r_ymm2, r_ymm3, r_ymm4, r_ymm5, r_ymm6, r_ymm7;
__m256 row0, row1, row2, row3, row4, row5, row6, row7;
__m256 ymm_even, ymm_odd, ymm_sum, ymm_diff;
__m256 temp3, temp7;
__m256 tangent_1, tangent_2, tangent_3, cos_4;
tangent_1 = AVX_tg_1_16;
tangent_2 = AVX_tg_2_16;
tangent_3 = AVX_tg_3p1_16;
cos_4 = AVX_cos_4p1_16;
const float * pInput;
float * pOutput;
float * pFTab_i_04 = float_tab_i_04;
float * pFTab_i_26 = float_tab_i_26;
float * pFTab_i_17 = float_tab_i_17;
float * pFTab_i_35 = float_tab_i_35;
const int blockSize = 8*8;
//すべてのブロックを N 回変換
//反復カウントはコマンドライン・オプション
const int maxLoopCount = g_loopCount;
long startTime = getTimestamp();
for(int loopCount = 0; loopCount < maxLoopCount; loopCount++) {
//すべてのブロックを処理
for(int i = 0; i < g_blockCount; i++) {
//この入力および出力のポインターを取得
pInput = &dctData[i*blockSize];
pOutput = &kernelResults[i*blockSize];
pFTab_i_04 = float_tab_i_04;
pFTab_i_26 = float_tab_i_26;
pFTab_i_17 = float_tab_i_17;
pFTab_i_35 = float_tab_i_35;
// IACA_START
//行 0 と 4
//2 つの行の最初の 4 つの float を処理
//2 つの 128 ビット・ロードで行 0 から 8 つの float を読み取り
r_ymm0 = _mm256_castps128_ps256(_mm_load_ps(pInput));
r_ymm1 = _mm256_castps128_ps256(_mm_load_ps(&pInput[4]));
//行 4 のデータを上位レーンに挿入
r_ymm0 = _mm256_insertf128_ps(r_ymm0, _mm_load_ps(&pInput[4*8]), 1);
r_ymm4 = _mm256_insertf128_ps(r_ymm1, _mm_load_ps(&pInput[4*8+4]), 1);
//float 0 をブロードキャスト
r_ymm1 = _mm256_shuffle_ps(r_ymm0, r_ymm0, 0x00);
//係数で乗算
r_ymm2 = _mm256_mul_ps(r_ymm1, *((__m256 *) pFTab_i_04));
//float 2 をブロードキャストして係数で乗算
r_ymm1 = _mm256_shuffle_ps(r_ymm0, r_ymm0, 0xaa);
r_ymm3 = _mm256_mul_ps(r_ymm1, *((__m256 *) &pFTab_i_04[8]));
//加算
r_ymm02 = _mm256_add_ps(r_ymm2, r_ymm3);
//float 1 をブロードキャストして係数で乗算
r_ymm1 = _mm256_shuffle_ps(r_ymm0, r_ymm0, 0x55);
r_ymm2 = _mm256_mul_ps(r_ymm1, *((__m256 *) &pFTab_i_04[16]));
//float 3 をブロードキャストして係数で乗算
r_ymm1 = _mm256_shuffle_ps(r_ymm0, r_ymm0, 0xff);
r_ymm3 = _mm256_mul_ps(r_ymm1, *((__m256 *) &pFTab_i_04[24]));
//加算
r_ymm13 = _mm256_add_ps(r_ymm2, r_ymm3);
//2 つの行の次の 4 つの float を処理
//float 4 をブロードキャスト
r_ymm1 = _mm256_shuffle_ps(r_ymm4, r_ymm4, 0x00);
//係数で乗算
r_ymm2 = _mm256_mul_ps(r_ymm1, *((__m256 *) &pFTab_i_04[32]));
//float 6 をブロードキャストして係数で乗算
r_ymm1 = _mm256_shuffle_ps(r_ymm4, r_ymm4, 0xaa);
r_ymm3 = _mm256_mul_ps(r_ymm1, *((__m256 *) &pFTab_i_04[40]));
//加算
r_ymm46 = _mm256_add_ps(r_ymm2, r_ymm3);
//float 5 をブロードキャストして係数で乗算
r_ymm1 = _mm256_shuffle_ps(r_ymm4, r_ymm4, 0x55);
r_ymm2 = _mm256_mul_ps(r_ymm1, *((__m256 *) &pFTab_i_04[48]));
//float 7 をブロードキャストして係数で乗算
r_ymm1 = _mm256_shuffle_ps(r_ymm4, r_ymm4, 0xff);
r_ymm3 = _mm256_mul_ps(r_ymm1, *((__m256 *) &pFTab_i_04[56]));
//加算で部分和を作成してから
//最終的な和と差を作成
r_ymm57 = _mm256_add_ps(r_ymm2, r_ymm3);
ymm_even = _mm256_add_ps(r_ymm02, r_ymm46);
ymm_odd = _mm256_add_ps(r_ymm13, r_ymm57);
ymm_diff = _mm256_sub_ps(ymm_even, ymm_odd);
ymm_sum = _mm256_add_ps(ymm_even, ymm_odd);
//差の順序を反転して出力 0 と 4 を作成
ymm_diff = _mm256_shuffle_ps(ymm_diff, ymm_diff, 0x1b);
row0 = _mm256_permute2f128_ps(ymm_sum, ymm_diff, 0x20);
row4 = _mm256_permute2f128_ps(ymm_sum, ymm_diff, 0x31);
//行 0 と 4 の処理はここまで
//行 1 と 7
//2 つの行の最初の 4 つの float を処理
//2 つの 128 ビット・ロードで行 1 から 8 つの float を読み取り
r_ymm0 = _mm256_castps128_ps256(_mm_load_ps(&pInput[8]));
r_ymm1 = _mm256_castps128_ps256(_mm_load_ps(&pInput[8+4]));
//行 7 のデータを上位レーンに挿入
r_ymm0 = _mm256_insertf128_ps(r_ymm0, _mm_load_ps(&pInput[7*8]), 1);
r_ymm4 = _mm256_insertf128_ps(r_ymm1, _mm_load_ps(&pInput[7*8+4]), 1);
//float 0 と 2 を処理
r_ymm1 = _mm256_shuffle_ps(r_ymm0, r_ymm0, 0x00);
r_ymm2 = _mm256_mul_ps(r_ymm1, *((__m256 *) pFTab_i_17));
r_ymm1 = _mm256_shuffle_ps(r_ymm0, r_ymm0, 0xaa);
r_ymm3 = _mm256_mul_ps(r_ymm1, *((__m256 *) &pFTab_i_17[8]));
r_ymm02 = _mm256_add_ps(r_ymm2, r_ymm3);
//float 1 と 3 を処理
r_ymm1 = _mm256_shuffle_ps(r_ymm0, r_ymm0, 0x55);
r_ymm2 = _mm256_mul_ps(r_ymm1, *((__m256 *) &pFTab_i_17[16]));
r_ymm1 = _mm256_shuffle_ps(r_ymm0, r_ymm0, 0xff);
r_ymm3 = _mm256_mul_ps(r_ymm1, *((__m256 *) &pFTab_i_17[24]));
r_ymm13 = _mm256_add_ps(r_ymm2, r_ymm3);
//2 つの行の次の 4 つの float を処理
//float 4 と 6 を処理
r_ymm1 = _mm256_shuffle_ps(r_ymm4, r_ymm4, 0x00);
r_ymm2 = _mm256_mul_ps(r_ymm1, *((__m256 *) &pFTab_i_17[32]));
r_ymm1 = _mm256_shuffle_ps(r_ymm4, r_ymm4, 0xaa);
r_ymm3 = _mm256_mul_ps(r_ymm1, *((__m256 *) &pFTab_i_17[40]));
r_ymm46 = _mm256_add_ps(r_ymm2, r_ymm3);
//float 5 と 7 を処理
r_ymm1 = _mm256_shuffle_ps(r_ymm4, r_ymm4, 0x55);
r_ymm2 = _mm256_mul_ps(r_ymm1, *((__m256 *) &pFTab_i_17[48]));
r_ymm1 = _mm256_shuffle_ps(r_ymm4, r_ymm4, 0xff);
r_ymm3 = _mm256_mul_ps(r_ymm1, *((__m256 *) &pFTab_i_17[56]));
r_ymm57 = _mm256_add_ps(r_ymm2, r_ymm3);
//最終的な和と差を作成
ymm_even = _mm256_add_ps(r_ymm02, r_ymm46);
ymm_odd = _mm256_add_ps(r_ymm13, r_ymm57);
ymm_diff = _mm256_sub_ps(ymm_even, ymm_odd);
ymm_sum = _mm256_add_ps(ymm_even, ymm_odd);
//差の順序を反転して出力 1 と 7 を作成
ymm_diff = _mm256_shuffle_ps(ymm_diff, ymm_diff, 0x1b);
row1 = _mm256_permute2f128_ps(ymm_sum, ymm_diff, 0x20);
row7 = _mm256_permute2f128_ps(ymm_sum, ymm_diff, 0x31);
//行 1 と 7 の処理はここまで
//行 2 と 6
//2 つの行の最初の 4 つの float を処理
//2 つの 128 ビット・ロードで行 2 から 8 つの float を読み取り
r_ymm0 = _mm256_castps128_ps256(_mm_load_ps(&pInput[2*8]));
r_ymm1 = _mm256_castps128_ps256(_mm_load_ps(&pInput[2*8+4]));
//行 6 のデータを上位レーンに挿入
r_ymm0 = _mm256_insertf128_ps(r_ymm0, _mm_load_ps(&pInput[6*8]), 1);
r_ymm4 = _mm256_insertf128_ps(r_ymm1, _mm_load_ps(&pInput[6*8+4]), 1);
//float 0 と 2 を処理
r_ymm1 = _mm256_shuffle_ps(r_ymm0, r_ymm0, 0x00);
r_ymm2 = _mm256_mul_ps(r_ymm1, *((__m256 *) pFTab_i_26));
r_ymm1 = _mm256_shuffle_ps(r_ymm0, r_ymm0, 0xaa);
r_ymm3 = _mm256_mul_ps(r_ymm1, *((__m256 *) &pFTab_i_26[8]));
r_ymm02 = _mm256_add_ps(r_ymm2, r_ymm3);
//float 1 と 3 を処理
r_ymm1 = _mm256_shuffle_ps(r_ymm0, r_ymm0, 0x55);
r_ymm2 = _mm256_mul_ps(r_ymm1, *((__m256 *) &pFTab_i_26[16]));
r_ymm1 = _mm256_shuffle_ps(r_ymm0, r_ymm0, 0xff);
r_ymm3 = _mm256_mul_ps(r_ymm1, *((__m256 *) &pFTab_i_26[24]));
r_ymm13 = _mm256_add_ps(r_ymm2, r_ymm3);
//2 つの行の次の 4 つの float を処理
//float 4 と 6 を処理
r_ymm1 = _mm256_shuffle_ps(r_ymm4, r_ymm4, 0x00);
r_ymm2 = _mm256_mul_ps(r_ymm1, *((__m256 *) &pFTab_i_26[32]));
r_ymm1 = _mm256_shuffle_ps(r_ymm4, r_ymm4, 0xaa);
r_ymm3 = _mm256_mul_ps(r_ymm1, *((__m256 *) &pFTab_i_26[40]));
r_ymm46 = _mm256_add_ps(r_ymm2, r_ymm3);
//float 5 と 7 を処理
r_ymm1 = _mm256_shuffle_ps(r_ymm4, r_ymm4, 0x55);
r_ymm2 = _mm256_mul_ps(r_ymm1, *((__m256 *) &pFTab_i_26[48]));
r_ymm1 = _mm256_shuffle_ps(r_ymm4, r_ymm4, 0xff);
r_ymm3 = _mm256_mul_ps(r_ymm1, *((__m256 *) &pFTab_i_26[56]));
r_ymm57 = _mm256_add_ps(r_ymm2, r_ymm3);
//最終的な和と差を作成
ymm_even = _mm256_add_ps(r_ymm02, r_ymm46);
ymm_odd = _mm256_add_ps(r_ymm13, r_ymm57);
ymm_diff = _mm256_sub_ps(ymm_even, ymm_odd);
ymm_sum = _mm256_add_ps(ymm_even, ymm_odd);
//差の順序を反転して出力 2 と 6 を作成
ymm_diff = _mm256_shuffle_ps(ymm_diff, ymm_diff, 0x1b);
row2 = _mm256_permute2f128_ps(ymm_sum, ymm_diff, 0x20);
row6 = _mm256_permute2f128_ps(ymm_sum, ymm_diff, 0x31);
//行 2 と 6 の処理はここまで
//行 3 と 5
//2 つの行の最初の 4 つの float を処理
//2 つの 128 ビット・ロードで行 3 から 8 つの float を読み取り
r_ymm0 = _mm256_castps128_ps256(_mm_load_ps(&pInput[3*8]));
r_ymm1 = _mm256_castps128_ps256(_mm_load_ps(&pInput[3*8+4]));
//行 5 のデータを上位レーンに挿入
r_ymm0 = _mm256_insertf128_ps(r_ymm0, _mm_load_ps(&pInput[5*8]), 1);
r_ymm4 = _mm256_insertf128_ps(r_ymm1, _mm_load_ps(&pInput[5*8+4]), 1);
//float 0 と 2 を処理
r_ymm1 = _mm256_shuffle_ps(r_ymm0, r_ymm0, 0x00);
r_ymm2 = _mm256_mul_ps(r_ymm1, *((__m256 *) pFTab_i_35));
r_ymm1 = _mm256_shuffle_ps(r_ymm0, r_ymm0, 0xaa);
r_ymm3 = _mm256_mul_ps(r_ymm1, *((__m256 *) &pFTab_i_35[8]));
r_ymm02 = _mm256_add_ps(r_ymm2, r_ymm3);
//float 1 と 3 を処理
r_ymm1 = _mm256_shuffle_ps(r_ymm0, r_ymm0, 0x55);
r_ymm2 = _mm256_mul_ps(r_ymm1, *((__m256 *) &pFTab_i_35[16]));
r_ymm1 = _mm256_shuffle_ps(r_ymm0, r_ymm0, 0xff);
r_ymm3 = _mm256_mul_ps(r_ymm1, *((__m256 *) &pFTab_i_35[24]));
r_ymm13 = _mm256_add_ps(r_ymm2, r_ymm3);
//2 つの行の次の 4 つの float を処理
//float 4 と 6 を処理
r_ymm1 = _mm256_shuffle_ps(r_ymm4, r_ymm4, 0x00);
r_ymm2 = _mm256_mul_ps(r_ymm1, *((__m256 *) &pFTab_i_35[32]));
r_ymm1 = _mm256_shuffle_ps(r_ymm4, r_ymm4, 0xaa);
r_ymm3 = _mm256_mul_ps(r_ymm1, *((__m256 *) &pFTab_i_35[40]));
r_ymm46 = _mm256_add_ps(r_ymm2, r_ymm3);
//float 5 と 7 を処理
r_ymm1 = _mm256_shuffle_ps(r_ymm4, r_ymm4, 0x55);
r_ymm2 = _mm256_mul_ps(r_ymm1, *((__m256 *) &pFTab_i_35[48]));
r_ymm1 = _mm256_shuffle_ps(r_ymm4, r_ymm4, 0xff);
r_ymm3 = _mm256_mul_ps(r_ymm1, *((__m256 *) &pFTab_i_35[56]));
r_ymm57 = _mm256_add_ps(r_ymm2, r_ymm3);
//最終的な和と差を作成
ymm_even = _mm256_add_ps(r_ymm02, r_ymm46);
ymm_odd = _mm256_add_ps(r_ymm13, r_ymm57);
ymm_diff = _mm256_sub_ps(ymm_even, ymm_odd);
ymm_sum = _mm256_add_ps(ymm_even, ymm_odd);
//差の順序を反転して出力 3 と 5 を作成
ymm_diff = _mm256_shuffle_ps(ymm_diff, ymm_diff, 0x1b);
row3 = _mm256_permute2f128_ps(ymm_sum, ymm_diff, 0x20);
row5 = _mm256_permute2f128_ps(ymm_sum, ymm_diff, 0x31);
//行 3 と 5 の処理はここまで
//******************************
//列の 1D IDCT を実行
//行を適切な正接値で乗算
//row5*(tangent3+1)
r_ymm0 = _mm256_mul_ps(row5, tangent_3);
//row3*(tangent3+1)
r_ymm1 = _mm256_mul_ps(row3, tangent_3);
//row7*tangent1
r_ymm4 = _mm256_mul_ps(row7, tangent_1);
//row1*tangent1
r_ymm5 = _mm256_mul_ps(row1, tangent_1);
//結果の作成を開始
//[row5*tangent3 + row5] + row3
r_ymm0 = _mm256_add_ps(r_ymm0, row3);
//row5 - [row1*tangent3 + row1]
r_ymm2 = _mm256_sub_ps(row5, r_ymm1);
//row6*tangent2
r_ymm7 = _mm256_mul_ps(row6, tangent_2);
//row2*tangent2
r_ymm3 = _mm256_mul_ps(row2, tangent_2);
//row1*tangent1 - row7
r_ymm5 = _mm256_sub_ps(r_ymm5, row7);
//row7*tangent1 + row1
r_ymm4 = _mm256_add_ps(r_ymm4, row1);
//後で入力として使用するため行 7 の中間結果を保存
//[row7*tangent1 + row1] + [row5*tangent3 + row3]
temp7 = _mm256_add_ps(r_ymm4, r_ymm0);
//後で入力として使用するため行 3 の中間結果を保存
//[row1*tangent1 - row7] + [row5 - [row1*tangent3 + row1]]
temp3 = _mm256_add_ps(r_ymm5, r_ymm2);
//[row7*tangent1 + row1] - [row5*tangent3 + row3]
r_ymm4 = _mm256_sub_ps(r_ymm4, r_ymm0);
//[row1*tangent1 - row7] - [row5 - [row1*tangent3 + row1]]
r_ymm5 = _mm256_sub_ps(r_ymm5, r_ymm2);
//{[row7*tangent1 + row1] - [row5*tangent3 + row3]} -
//{[row1*tangent1 - row7] - [row5 - [row1*tangent3 + row1]]}
r_ymm1 = _mm256_sub_ps(r_ymm4, r_ymm5);
//{[row7*tangent1 + row1] - [row5*tangent3 + row3]} +
//{[row1*tangent1 - row7] - [row5 - [row1*tangent3 + row1]]}
r_ymm4 = _mm256_add_ps(r_ymm4, r_ymm5);
//cos_4+1 で行算
r_ymm4 = _mm256_mul_ps(r_ymm4, cos_4);
//row6*tangent2 + row2
r_ymm7 = _mm256_add_ps(r_ymm7, row2);
//row2*tangent2 - row6
r_ymm3 = _mm256_sub_ps(r_ymm3, row6);
//cos_4+1 で行算
r_ymm0 = _mm256_mul_ps(r_ymm1, cos_4);
//row0 + row4
r_ymm5 = _mm256_add_ps(row0, row4);
//row0 - row4
r_ymm6 = _mm256_sub_ps(row0, row4);
//[row0 + row4] - [row6*tangent2 + row2]
r_ymm2 = _mm256_sub_ps(r_ymm5, r_ymm7);
//[row0 + row4] + [row6*tangent2 + row2]
r_ymm5 = _mm256_add_ps(r_ymm5, r_ymm7);
//[row0 - row4] - [row2*tangent2 - row6]
r_ymm1 = _mm256_sub_ps(r_ymm6, r_ymm3);
//[row0 - row4] + [row2*tangent2 - row6]
r_ymm6 = _mm256_add_ps(r_ymm6, r_ymm3);
//[[row7*tangent1 + row1] + [row5*tangent3 + row3]] +
//[[row0 + row4] + [row6*tangent2 + row2]]
r_ymm7 = _mm256_add_ps(temp7, r_ymm5);
//行 0 の結果を格納 (1/8)
_mm256_store_ps(pOutput, r_ymm7);
//[[row0 - row4] + [row2*tangent2 - row6]] -
//cos4*{[row7*tangent1 + row1] - [row5*tangent3 + row3]} +
//{[row1*tangent1 - row7] - [row5 - [row1*tangent3 + row1]]}
r_ymm3 = _mm256_sub_ps(r_ymm6, r_ymm4);
//[[row0 - row4] + [row2*tangent2 - row6]] +
//cos4*{[row7*tangent1 + row1] - [row5*tangent3 + row3]} +
//{[row1*tangent1 - row7] - [row5 - [row1*tangent3 + row1]]}
r_ymm6 = _mm256_add_ps(r_ymm6, r_ymm4);
//行 1 の結果を格納 (2/8)
_mm256_store_ps(&pOutput[1*8], r_ymm6);
r_ymm7 = _mm256_sub_ps(r_ymm1, r_ymm0);
r_ymm1 = _mm256_add_ps(r_ymm1, r_ymm0);
r_ymm6 = _mm256_add_ps(r_ymm2, temp3);
r_ymm2 = _mm256_sub_ps(r_ymm2, temp3);
r_ymm5 = _mm256_sub_ps(r_ymm5, temp7);
//最終的な結果を格納
_mm256_store_ps(&pOutput[2*8], r_ymm1);
_mm256_store_ps(&pOutput[3*8], r_ymm6);
_mm256_store_ps(&pOutput[4*8], r_ymm2);
_mm256_store_ps(&pOutput[5*8], r_ymm7);
_mm256_store_ps(&pOutput[6*8], r_ymm3);
_mm256_store_ps(&pOutput[7*8], r_ymm5);
// IACA_END
}
}
long duration = getTimestamp() - startTime;
cout << "AVX Timestamp = " << duration << endl;
}
参考文献 (英語)
この記事では、以下の文献を参照しています。これらの文献には、この記事で説明している内容を理解するための背景情報が記述されています。
1. Pennebaker and Mitchell, JPEG: Still Image Data Compression Standard, Van Nostrand Reinhold, New York, 1993, pp. 29-64.
2. A Fast Precise Implementation of 8x8 Discrete Cosine Transform Using the Streaming SIMD Extensions and MMXTM Instructions, Intel Application Note, AP-922, Copyright 1999
3. Using Streaming SIMD Extensions 2 (SSE2) to Implement and Inverse Discrete Cosine Transform, Intel Application Note, AP-945, Copyright 2000
4. Rao and Yip, Discrete Cosine Transform Algorithms, Advantages, Applications, Academic Press, Inc., Boston, 1990, Appendix A.2
5. IEEE Standard Specifications for the Implementations of 8x8 Inverse Discrete Cosine Transform, IEEE Std 1180-1990.
著者紹介
Richard Hubbard: インテルのシニア・ソフトウェア・エンジニア。SSG Apple enabling チームのメンバーで、Mac OS X* アプリケーションの電力効率とパフォーマンスの最適化に取り組んでいます。Stevens Institute of Technology で電気工学の修士号、New Jersey Institute of Technology でコンピューター・エンジニアリングの学士号を取得しています。
インテル® ソフトウェア製品のパフォーマンス/最適化に関する詳細は、最適化に関する注意事項 (英語) を参照してください。
編集部追加
第2世代インテル® Core™ プロセッサーファミリーに搭載されているインテル® AVX を活用するには、コンパイラーのサポートが不可欠です。まだインテル® コンパイラーをお持ちでない方は、是非ともインテル® C++ Composer XE の評価版をご利用いただき、本記事のサンプルコードにてインテル® AVX によるパフォーマンス向上を実感してください。評価版のダウンロード、お問い合わせはエクセルソフト株式会社まで。


