この記事は、インテル® ソフトウェア・ネットワークに掲載されている「Benefits of Intel® Advanced Vector Extensions For Quaternion Spherical Linear Interpolation (Slerp)」(http://software.intel.com/en-us/articles/benefits-of-intel-advanced-vector-extensions-for-quaternion-spherical-liner-interpolation-slerp/) の日本語参考訳です。
はじめに
インテル® アドバンスト・ベクトル・エクステンション (インテル® AVX) は、新しいインテル® マイクロアーキテクチャー (Sandy Bridge) で導入され、特に浮動小数点データのロードとストアおよび演算において、インテル® ストリーミング SIMD 拡張命令 (インテル® SSE) の機能を拡張します。インテル® AVX における YMM レジスターは、現在の XMM レジスターの 2 倍の幅があり、より広いデータ幅で演算を行うことができます。以前の 128 ビットの SIMD 命令セットの拡張と比べて電力効率に優れており、浮動小数点のパフォーマンス密度を向上させます。
ここでは、インテル® AVX と新しいインテル® マイクロアーキテクチャー (Sandy Bridge) のさまざまな機能 (よりワイドな 256 ビットの SIMD レジスター、異なるデスティネーション、新しいデータ操作と演算プリミティブ、2 つの 128 ビット・ロード・ポート、計算実行幅の倍増など) が 4 次元データセットの球面線形補間 (SLERP) 処理にどのように役立つかについて説明します。
インテルでは、インテル® AVX 対応のコンパイラー、インテル® ソフトウェア・デベロップメント・エミュレーター (インテル® SDE)、インテル® アーキテクチャー・コード・アナライザーなどのインテル® AVX ソフトウェア開発ツールも提供しています。これらのツールはすべて、このカーネルの開発中に使用されました。ツールは、インテル® AVX Web サイト (http://software.intel.com/en-us/avx/) からダウンロードできます。
テスト環境
ここで紹介するパフォーマンス・データは、新しいインテル®マイクロアーキテクチャー (Sandy Bridge) ベースの CPU 上で実行した値を測定したものです。また、Slerp アルゴリズムの演算を開始する前に、プロセッサーの 1 次キャッシュにテストデータがロードされていると仮定しています。パフォーマンスの比較は、C 組込み関数を使用してインテル® AVX と対応するインテル® SSE 実装を実行したときの相対的なパフォーマンスに基づいて行われています。コードはインテル® C++ コンパイラー 11.0.074 でコンパイルされています。
3D における方向の表現
3D グラフィックスでは、方向をオイラー角、回転行列、クォータニオン (四元数) として表します。座標空間の変換や地点間の補間は一般的なグラフィックス処理です。座標空間の方向ベクトルを変換および回転する場合は行列を使用します。クォータニオンで球面線形補間を行うと、方向を最も滑らかに補間できます。
クォータニオンは小さく効率的で、回転行列よりも簡単です。3×3 の回転行列には 9 つの値が必要ですが、クォータニオンには 4 つの値しか必要ありません。クォータニオンの乗算も行列の乗算より効率的です。また、クォータニオンは必要なときに行列に簡単に変換できます。オイラー角で問題となる「ジンバルロック」もクォータニオンを使用することで回避できます。これらの特性により、クォータニオンは、多くの (例えば、3D アニメーションで使用される) アルゴリズムで理想的なものとして使用されています。クォータニオンの説明、および回転行列とクォータニオンの変換については、参考文献 [2] を参照してください。
クォータニオン Slerp
アニメーション・システムは、キーフレーム間の回転を行うときによく補間を行います。異なるアニメーションを加えて、あるアニメーションから別のアニメーションへの移行を滑らかにすることもあります。クォータニオンによる補間には、球面線形補間 (Slerp)、線形補間 (Lerp) と再正規化、対数写像による補間の 3 つの一般的なアプローチがあります。これらのうち、Slerp が 2 つの一般的な回転を最も適切に補間できると考えられています。Slerp アルゴリズムにはいくつかの三角関数が含まれていて、大量の演算が行われます。
クォータニオン q0 および q1、パラメーター t、範囲 [0, 1] で指定すると、球面線形補間は次のように定義されます。
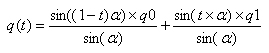
α は q0 と q1 間の角で、2 つのクォータニオンの内積から求めることができます。
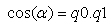
参考文献 [1] では、スカラー実装と SIMD 実装で使用した最適化 Slerp アルゴリズムを詳細に説明しています。
先行研究
この記事のインテル® AVX 実装で使用されている Slerp アルゴリズムは、参考文献 [J.M.P.van Waveren, Slerping Clock Cycles, Id Software, Inc. 2005] で説明されている最適化アルゴリズムに従っています。まず、インテル® SSE コードを C 組込み関数に移植した後、インテル® AVX に移植しました。
クォータニオン Slerp のインテル® AVX 実装
参考文献のインテル® SSE 実装と同様に、インテル® AVX 実装でも、2 つのクォータニオン間に球面線形補間を使用する代わりに、クォータニオン・リスト間を補間します。例えば、スケルトン・アニメーション・システムでは通常、2 つのキーフレーム間の補間が必要になります。各キーフレームは、スケルトンの姿勢を定義するジョイントを含むリストです。キーフレームのジョイントの方向はクォータニオン、位置は 4D ベクトルとして格納されます。
Slerp アルゴリズムのインテル® SSE からインテル® AVX への移植は難しくありません。特に最適化を加えることなく、最初の移植で 1.58 倍のスピードアップを達成しています。いくつかの最適化を適用することで、より高いパフォーマンス・レベルが得られます。
元のアルゴリズムを注意深く確認すると、最初の乗算の後に置き換え (swizzle) を行うことで、命令数を減らせることが分かります。両方の入力クォータニオンを最初に置き換えてから乗算する代わりに、先に乗算してから置き換えることで、4 つの _mm256_unpackxx_ps および 4 つの _mm256_unpackxx_pd 命令を排除できます。
置き換え操作に別の最適化を行うことで、命令数をさらに減らすこともできます。すべての要素をシーケンシャルに整列する完全な置き換えは必要ないため、この最適化は有効です。デスティネーション・レジスター内で同じ順で要素を整列するには、この最適化で十分です。この最適化は、まず、_mm256_load_ps 命令を使用し、メモリーから 8 つのクォータニオンを読み込んで 4 つの ymm レジスターにロードします。次の図は、X コンポーネントがクォータニオンのセットからどのように 1 つのレジスターに集約されるかを示しています。同様の操作を行って、Y、Z、W コンポーネントを集めます。このアプローチにより、シャッフルポートで実行する命令の数は 36 から 24 に減りました。
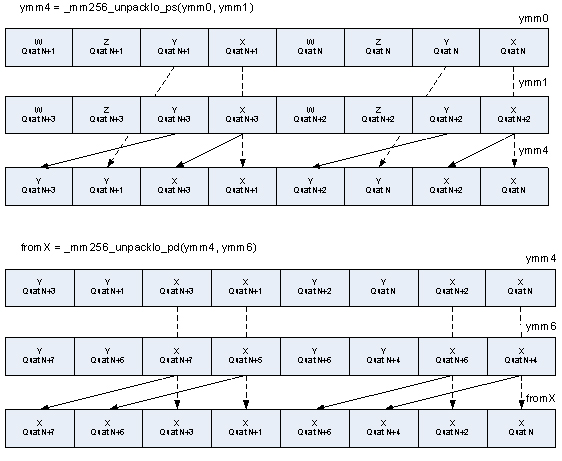
コンポーネントが適切な場所に格納できたら、SLERP 処理を実行します。同様の操作を適用して、各クォータニオンのすべてのコンポーネントを集めます。その後、結果をメモリーに書き込みます。
for ループを一回だけアンロールする (つまり、ループごとに 16 セットのクォータニオンで SLERP 処理を実行する) 最適化も有効です。この最適化を行うことで、回数を制限しないでアンロールしたインテル® AVX バージョンよりも 2.4% パフォーマンスが向上しました。
命令を再整列することが効果的な例はいくつかあります。例えば、アルゴリズムの最初の積和では、2 つ目の部分和で使用されるオペランドが置き換えられる前に、1 つ目の部分和を計算できます。
メモリーのアライメントも重要です。_mm256_loadu_ps の代わりに _mm256_load_ps を使用することでパフォーマンスを向上できます。このため、32 ビット境界で 256 ビット・オペランドのアライメントを行うことを強く推奨します。これは、このコードを使用する場合はアライメントされたデータを渡す必要があることを意味します。データのアライメントが保証されない場合、非アライメント・バージョンのロードとストア命令を使用する必要があります。コンパイラーによって生成されたコードを調査して、最も効率的なメモリーアクセスを行うロードとストア命令を選択すると良いでしょう。
インテル® アーキテクチャー・コード・アナライザーは、クリティカル・パス命令を識別して、実行ポートの使用状況に関する情報を提供します。この解析ツールを使用することで、開発者はアルゴリズムの実装に最適な命令を選択することができます。
結果
128 ビットのコードは、以前のインテル® マイクロアーキテクチャー (Nehalem) 向けにコンパイルされたインテル® SSE コードを新しいインテル® マイクロアーキテクチャー (Sandy Bridge) ベースのシステムで実行したものです。対応する 256 ビットのコードは、新しいインテル® マイクロアーキテクチャー (Sandy Bridge) 向けにコンパイルされたインテル® AVX 対応のコードを、新しいインテル® マイクロアーキテクチャー (Sandy Bridge) ベースのシステムで実行したものです。データは、インテル® SSE コードでは 16 ビット境界、インテル® AVX コードでは 32 ビット境界でそれぞれアライメントされています。次の表のスピードアップは、256 ビット・コードと対応する 128 ビット・コードを比較した値を示しています。
通常は、128 ビットのインテル® SSE 命令から 256 ビットのインテル® AVX 命令に変更しても 2 倍以上のパフォーマンスの向上は見込めないことに注意してください。ここでは、インテル® SSE バージョンで適用されなかった最適化がインテル® AVX バージョンで行われているため、結果は 2 倍を少し上回っています。インテル® SSE バージョンは、オリジナルのホワイトペーパー [J.M.P.van Waveren, Slerping Clock Cycles, Id Software, Inc. 2005] に基づいており、追加の最適化は行われていません。唯一の違いは、インテル® AVX とのスピードアップの比較のために、オリジナルのホワイトペーパーではアセンブリーで記述されていたインテル® SSE コードが C 組込み関数に変換されていることです。
16 の倍数のデータセットでは、インテル® AVX で 2.16 倍のスピードアップが達成されました。これは、インテル® AVX コードではインテル® SSE の 2 倍の浮動小数点データを処理できることと、反復ごとに 16 の要素を処理できる 1 ウェイのループアンロールを行っているためです。
16 の倍数でないデータセットでは、個々のループで非モジュロ要素を処理する必要があります。この 2 つ目のループは、単純な C スカラーコードとして現在処理されています。ただし、配列境界を超えることなく、条件付きで特定の配列要素のみをロードおよびストアできるインテル® AVX のマスク移動命令を使用してさらに最適化することができます。
| アルゴリズム | スピードアップ | パラメーター |
| クォータニオン Slerp (16 の倍数のみ) | 2.16 倍 | ソースは 2 セットのクォータニオン (セットごとに 64) |
| クォータニオン Slerp (16 の倍数以外を含む) | 1.86 倍 | ソースは 2 セットのクォータニオン (セットごとに 67) |
表 1 – 256 ビットのコードと 128 ビットのコードを比べたスピードアップ
インテル® アーキテクチャー・コード・アナライザーの相関性
インテル® アーキテクチャー・コード・アナライザーは、実行ポートの使用率について命令のブロックを解析し、スループットのボトルネックを識別するツールです。このツールは、アルゴリズムのさまざまなステップにおける実行ポート 5 の使用率を解析するため、Slerp カーネルの開発中に効率的に使用されました。
コード・アナライザーは、スピードアップの予想にも使用できます。Slerp カーネルの場合、コード・アナライザーは、スピードアップがシリコンのスピードアップの 4% 以内であると予想しました。ただし、コード・アナライザーの結果がシリコンの結果と非常に近いことは稀であることに注意してください。インテル® アーキテクチャー・コード・アナライザーは、データがすべてレベル 1 キャッシュに存在しており、動的なマイクロアーキテクチャーのペナルティーがないと仮定してモデル化されています。このため、ツールは、単にスピードアップの予想を確認する方法の 1 つとして使用してください。
Intel© Architecture Code Analyzer Intel® SSE throughput analysis report:
----------------------------------------------------------------------------
Block Throughput: 47.75 Cycles Throughput Bottleneck: Port0
Port Binding In Cycles Per Iteration:
-----------------------------------------------------------------------------
| Port | 0 - DV | 1 | 2 - D | 3 - D | 4 | 5 |
-----------------------------------------------------------------------------
| Cycles | 46.0 0.0 | 34.0 | 19.5 16.5 | 19.5 16.5 | 6.0 | 33.0 |
-----------------------------------------------------------------------------
Intel© Architecture Code Analyzer Intel® AVX throughput analysis report:
-----------------------------------------------------------------------------
Block Throughput: 97.20 Cycles Throughput Bottleneck: Port0
Port Binding In Cycles Per Iteration:
-----------------------------------------------------------------------------
| Port | 0 - DV | 1 | 2 - D | 3 - D | 4 | 5 |
-----------------------------------------------------------------------------
| Cycles | 96.0 0.0 | 68.0 | 33.5 56.0 | 33.5 56.0 | 22.0 | 61.0 |
-----------------------------------------------------------------------------
注: 上記のコード・アナライザーの統計を収集するため、16 の倍数であるクォータニオンを処理する最初のループは、ループ内部の命令ブロックの最初と最後に IACA_START および IACA_END マーカーを挿入しています。
64 クォータニオンの場合、
インテル® アーキテクチャー・コード・アナライザーが測定したインテル® SSE のカウント = 47.75 * 64/4 = 764 サイクル
インテル® アーキテクチャー・コード・アナライザーが測定したインテル® AVX のカウント = 97.20 * 64/16 = 368.5 サイクル
インテル® アーキテクチャー・コード・アナライザーが予想したスピードアップ = インテル® SSE のカウント/ インテル® AVX のカウント = 2.07 倍
予想されたスピードアップは、実際のインテル®マイクロアーキテクチャー (Sandy Bridge) で測定したスピードアップの 4% 以内です。
まとめ
2 セットのアライメントされたクォータニオンのデータに球面線形補間を行ったところ、インテル® AVX バージョンでは、元のインテル® SSE バージョンの 2.16 倍のスピードアップが達成されました。このアルゴリズムは、インテル® AVX のほうが、レジスターの幅を活用することで 1 命令あたり 2 倍のオペランドを処理し、インテル® SSE よりも高いスループットを達成できることを示しています。
このアルゴリズムは、8 つのクォータニオンで同時に Slerp 計算を実行し、インテル® AVX SIMD アーキテクチャーを活用することで、高いスループットを実現しています。メモリー操作よりも計算比率が高い命令を使用することも有効です。追加の最適化として、単純なループのアンロールと、よりレイテンシーが大きな計算命令の前にアンロールした反復からロードを行う手動スケジューリングを行いました。メインの計算ループの外ですべての定数を初期化することで、インテル® AVX のパフォーマンスをさらに向上させることができます。
クォータニオン Slerp のソースコード
クォータニオン SLERP の完全なソースコードは、http://software.intel.com/file/24886 からダウンロードできます。
ソースコードの一部を以下に示します。
//Some constants needed when calculating sin(x)
#define SINC0 -2.39e-08f
#define SINC1 2.7526e-06f
#define SINC2 -1.98409e-04f
#define SINC3 8.3333315e-03f
#define SINC4 -1.666666664e-01f
//Some constants needed for Newton-Rapson iteration
#define RSQRT_C0 3.0f
#define RSQRT_C1 -0.5f
//Some constants needed when calculating arc tangent
#define ATANC0 0.0028662257f
#define ATANC1 -0.0161657367f
#define ATANC2 0.0429096138f
#define ATANC3 -0.0752896400f
#define ATANC4 0.1065626393f
#define ATANC5 -0.1420889944f
#define ATANC6 0.1999355085f
#define ATANC7 -0.3333314528f
//General purpose constants
#define ALL_ONES 1.0f
#define CLEAR_SIGN_BIT 0x7fffffff
#define SET_SIGN_BIT 0x80000000
#define HALF_PI (float) (22.0f/7.0f/2.0f)
#define TINY 0.1e-09f
#define DECLARE_INIT_M256(name, value) __m256 name = {value, value, value, value, value, value, value, value};
#define DECLARE_INIT_M256I(name, value) __m256i name = {value, value, value, value, value, value, value, value};
//Initialize constants
DECLARE_INIT_M256(sinC0, SINC0);
DECLARE_INIT_M256(sinC1, SINC1);
DECLARE_INIT_M256(sinC2, SINC2);
DECLARE_INIT_M256(sinC3, SINC3);
DECLARE_INIT_M256(sinC4, SINC4);
DECLARE_INIT_M256(sqrtC0, RSQRT_C0);
DECLARE_INIT_M256(sqrtC1, RSQRT_C0);
DECLARE_INIT_M256(atanC0, ATANC0);
DECLARE_INIT_M256(atanC1, ATANC1);
DECLARE_INIT_M256(atanC2, ATANC2);
DECLARE_INIT_M256(atanC3, ATANC3);
DECLARE_INIT_M256(atanC4, ATANC4);
DECLARE_INIT_M256(atanC5, ATANC5);
DECLARE_INIT_M256(atanC6, ATANC6);
DECLARE_INIT_M256(atanC7, ATANC7);
DECLARE_INIT_M256(allOnes, ALL_ONES);
DECLARE_INIT_M256(halfPi, HALF_PI);
DECLARE_INIT_M256(tiny, TINY);
DECLARE_INIT_M256I(dClearSignBit, CLEAR_SIGN_BIT);
DECLARE_INIT_M256I(dSetSignBit, SET_SIGN_BIT);
DECLARE_INIT_M256(clearSignBit, 0);
DECLARE_INIT_M256(setSignBit, 0);
//Application initialization - call once before invoking slerp
void initializationFunction(void) {
//Initialize some constants
clearSignBit = _mm256_castsi256_ps(dClearSignBit);
setSignBit = _mm256_castsi256_ps(dSetSignBit);
}
//Perform the SLERP operation
void ProcessOptimizedKernel(void) {
__m256 fromX, fromY, fromZ, fromW, toX, toY, toZ, toW, factor;
__m256 cosom, absCosom, sinsqr, sinom;
__m256 ymmR0, ymmR1, ymmR2, ymmR3, ymmR4, ymmR5, ymmR6, ymmR7;
__m256 scale0, scale1;
__m256 signBit;
__m256 omega;
float * pFromQuat;
float * pToQuat;
float * pResults;
//Initialize data in and out pointers
pFromQuat = (float *) fromQuaternion;
pToQuat = (float *) toQuaternion;
pResults = (float *) resultQuaternion;
//Other initializations
factor = _mm256_broadcast_ss(&g_factor);
int mod16QuaternionCount = g_quaternionCount & 0xfffffff0;
//Operate on all the quaternions
for(int i = 0; i < mod16QuaternionCount; i += 16) {
//Load From-Quat 0 and Quat 1 into one register
fromX = _mm256_load_ps(pFromQuat + i/8*32);
//Load From-Quat 2 and Quat 3 into one register
fromY = _mm256_load_ps(pFromQuat + i/8*32 + 2*4);
//Load From-Quat 4 and Quat 5 into one register
fromZ = _mm256_load_ps(pFromQuat + i/8*32 + 4*4);
//Load From-Quat 6 and Quat 7 into one register
fromW = _mm256_load_ps(pFromQuat + i/8*32 + 6*4);
//Load To-Quat 0 and Quat 1 into one register
toX = _mm256_load_ps(pToQuat + i/8*32);
//Load To-Quat 2 and Quat 3 into one register
toY = _mm256_load_ps(pToQuat + i/8*32 + 2*4);
//Load To-Quat 4 and Quat 5 into one register
toZ = _mm256_load_ps(pToQuat + i/8*32 + 4*4);
//Load To-Quat 6 and Quat 7 into one register
toW = _mm256_load_ps(pToQuat + i/8*32 + 6*4);
//*** Compute product terms: fromx*tox, fromy*toy, fromz*toz, fromw*tow
//ymmR0 = fromw1*tow1, fromz1*toz1, fromy1*toy1, fromx1*tox
// fromw0*tow0, fromz0*toz0, fromy0*toy0, fromx0*tox0
ymmR0 = _mm256_mul_ps(fromX, toX); //Quaternion 0 and 1
ymmR1 = _mm256_mul_ps(fromY, toY); //Quaternion 2 and 3
ymmR2 = _mm256_mul_ps(fromZ, toZ); //Quaternion 4 and 5
ymmR3 = _mm256_mul_ps(fromW, toW); //Quaternion 6 and 7
//*** Swizzle products to prepare for additions
//Start collecting product terms (step 1 of 2)
//Get y3, y1, x3, x1, y2, y0, x2, x0
ymmR4 = _mm256_unpacklo_ps(ymmR0, ymmR1);
//Get w3, w1, z3, z1, w2, w0, z2, z0
ymmR5 = _mm256_unpackhi_ps(ymmR0, ymmR1);
//Get y7, y5, x7, x5, y6, y4, x6, x4
ymmR6 = _mm256_unpacklo_ps(ymmR2, ymmR3);
//Get w7, w5, z7, z5, w6, w4, z6, z4
ymmR7 = _mm256_unpackhi_ps(ymmR2, ymmR3);
//Finish collecting product terms (step 2 of 2)
//Get x7, x5, x3, x1, x6, x4, x2, x0
ymmR0 = _mm256_castpd_ps(_mm256_unpacklo_pd(_mm256_castps_pd(ymmR4), _mm256_castps_pd(ymmR6)));
//Get y7, y5, y3, y1, y6, y4, y2, y0
ymmR1 = _mm256_castpd_ps(_mm256_unpackhi_pd(_mm256_castps_pd(ymmR4), _mm256_castps_pd(ymmR6)));
//calculate first partial sum
ymmR4 = _mm256_add_ps(ymmR0, ymmR1);
//Get z7, z5, z3, z1, z6, z4, z2, z0
ymmR2 = _mm256_castpd_ps(_mm256_unpacklo_pd(_mm256_castps_pd(ymmR5), _mm256_castps_pd(ymmR7)));
//Get w7, w5, w3, w1, w6, w4, w2, w0
ymmR3 = _mm256_castpd_ps(_mm256_unpackhi_pd(_mm256_castps_pd(ymmR5), _mm256_castps_pd(ymmR7)));
//Finish adding the terms
//Second partial sum
ymmR5 = _mm256_add_ps(ymmR2, ymmR3);
//Final sum
cosom = _mm256_add_ps(ymmR4, ymmR5);
//*** Compute the absolute value of above
absCosom = _mm256_and_ps(cosom, clearSignBit);
//Save the sign bit, used to invert scale1 later
signBit = _mm256_and_ps(cosom, setSignBit);
//*** Compute 1.0 - (above squared)
ymmR0 = _mm256_mul_ps(absCosom, absCosom);
sinsqr = _mm256_sub_ps(allOnes, ymmR0);
//Watch for very small values
ymmR1 = _mm256_xor_ps(ymmR1, ymmR1); //Zeros
ymmR1 = _mm256_cmpeq_ps(ymmR1, sinsqr);
ymmR1 = _mm256_and_ps(ymmR1, tiny); //Make them tiny, not zero
sinsqr = _mm256_and_ps(sinsqr, clearSignBit);//Make them positive
sinsqr = _mm256_or_ps(sinsqr, ymmR1);
//Compute 1/(square root of above)
sinom = _mm256_rsqrt_ps(sinsqr);
ymmR0 = _mm256_mul_ps(sinsqr, sinom);
ymmR0 = _mm256_mul_ps(ymmR0, sinom);
ymmR0 = _mm256_sub_ps(ymmR0, sqrtC0);
ymmR1 = _mm256_mul_ps(sinom, sqrtC1);
ymmR0 = _mm256_mul_ps(ymmR0, ymmR1);
ymmR0 = _mm256_mul_ps(sinsqr, sinom);
//*** Compute the ArcTangent (omega = arctan(sinom*sinsqr, absCosom))
ymmR1 = absCosom;
absCosom = _mm256_min_ps(absCosom, ymmR0);
ymmR0 = _mm256_max_ps(ymmR0, ymmR1);
ymmR1 = _mm256_cmpeq_ps(ymmR1, absCosom);
ymmR2 = _mm256_rcp_ps(ymmR0);
ymmR0 = _mm256_mul_ps(ymmR0, ymmR2);
ymmR0 = _mm256_mul_ps(ymmR0, ymmR2);
ymmR2 = _mm256_add_ps(ymmR2, ymmR2);
ymmR2 = _mm256_sub_ps(ymmR2, ymmR0);
absCosom = _mm256_mul_ps(absCosom, ymmR2);
ymmR0 = ymmR1; //copy the mask
ymmR0 = _mm256_and_ps(ymmR0, setSignBit/*ymmR2*/);
absCosom = _mm256_xor_ps(absCosom, ymmR0);
//cmp mask determines contents: Pi/2 or 0.0
ymmR1 = _mm256_and_ps(ymmR1, halfPi);
//finish ArcTangent calculation
ymmR0 = _mm256_mul_ps(absCosom, absCosom);
ymmR2 = _mm256_mul_ps(atanC0, ymmR0);
ymmR2 = _mm256_add_ps(ymmR2, atanC1);
ymmR2 = _mm256_mul_ps(ymmR2, ymmR0);
ymmR2 = _mm256_add_ps(ymmR2, atanC2);
ymmR2 = _mm256_mul_ps(ymmR2, ymmR0);
ymmR2 = _mm256_add_ps(ymmR2, atanC3);
ymmR2 = _mm256_mul_ps(ymmR2, ymmR0);
ymmR2 = _mm256_add_ps(ymmR2, atanC4);
ymmR2 = _mm256_mul_ps(ymmR2, ymmR0);
ymmR2 = _mm256_add_ps(ymmR2, atanC5);
ymmR2 = _mm256_mul_ps(ymmR2, ymmR0);
ymmR2 = _mm256_add_ps(ymmR2, atanC6);
ymmR2 = _mm256_mul_ps(ymmR2, ymmR0);
ymmR2 = _mm256_add_ps(ymmR2, atanC7);
ymmR2 = _mm256_mul_ps(ymmR2, ymmR0);
ymmR2 = _mm256_add_ps(ymmR2, allOnes);
ymmR2 = _mm256_mul_ps(ymmR2, absCosom);
//Adjust by adding Pi/2 or 0.0
omega = _mm256_add_ps(ymmR2, ymmR1);
//*** Compute the first scale factor
//Compute [1.0 - (move factor)]*above?
ymmR1 = _mm256_mul_ps(factor, omega);
ymmR0 = _mm256_sub_ps(omega, ymmR1);
//Compute both scale factors
//Compute sin(above)
ymmR1 = ymmR0; //used to calculate scale0
//Compute factor*omega
ymmR6 = _mm256_mul_ps(factor, omega);
ymmR4 = ymmR6; //used to calculate scale1
ymmR1 = _mm256_mul_ps(ymmR1, ymmR1);
ymmR4 = _mm256_mul_ps(ymmR4, ymmR4); //scale1
ymmR2 = _mm256_mul_ps(sinC0, ymmR1);
ymmR5 = _mm256_mul_ps(sinC0, ymmR4); //scale1
ymmR2 = _mm256_add_ps(ymmR2, sinC1);
ymmR2 = _mm256_mul_ps(ymmR2, ymmR1);
ymmR5 = _mm256_add_ps(ymmR5, sinC1); //scale1
ymmR5 = _mm256_mul_ps(ymmR5, ymmR4); //scale1
ymmR2 = _mm256_add_ps(ymmR2, sinC2);
ymmR2 = _mm256_mul_ps(ymmR2, ymmR1);
ymmR5 = _mm256_add_ps(ymmR5, sinC2); //scale1
ymmR5 = _mm256_mul_ps(ymmR5, ymmR4); //scale1
ymmR2 = _mm256_add_ps(ymmR2, sinC3);
ymmR2 = _mm256_mul_ps(ymmR2, ymmR1);
ymmR5 = _mm256_add_ps(ymmR5, sinC3); //scale1
ymmR5 = _mm256_mul_ps(ymmR5, ymmR4); //scale1
ymmR2 = _mm256_add_ps(ymmR2, sinC4);
ymmR2 = _mm256_mul_ps(ymmR2, ymmR1);
ymmR5 = _mm256_add_ps(ymmR5, sinC4); //scale1
ymmR5 = _mm256_mul_ps(ymmR5, ymmR4); //scale1
ymmR2 = _mm256_add_ps(ymmR2, allOnes);
ymmR2 = _mm256_mul_ps(ymmR2, ymmR0); //ymmR2 has the sin(x) for eight
ymmR5 = _mm256_add_ps(ymmR5, allOnes); //scale1
ymmR5 = _mm256_mul_ps(ymmR5, ymmR6); //ymmR5 has the sin(x) for eight
//Compute above*sinom
scale0 = _mm256_mul_ps(ymmR2, sinom); //scale0 has the first scale factor
scale1 = _mm256_mul_ps(ymmR5, sinom); //scale1 has the second scale factor
//*** invert the second scale factor if that first sum of products is negative
scale1 = _mm256_xor_ps(scale1, signBit);
//*** Compute the final results by scaling
//Copy scale values for quat 1 and 0 to all spots in their 128-bit lane
//ymmR6 = scale01, scale01, scale01, scale01, scale00, scale00, scale00, scale00
ymmR6 = _mm256_shuffle_ps(scale0, scale0, 0x00);
//ymmR7 = scale11, scale11, scale11, scale11, scale10, scale10, scale10, scale10
ymmR7 = _mm256_shuffle_ps(scale1, scale1, 0x00);
//Scale the original From quaternions 1 and 0
ymmR0 = _mm256_mul_ps(ymmR6, fromX);
//Scale the original To quaternions 1 and 0
ymmR1 = _mm256_mul_ps(ymmR7, toX);
//Add to complete the SLERP, then store results to memory.
ymmR2 = _mm256_add_ps(ymmR0, ymmR1); //ymmR2 has all the quat 0 and 1 results
_mm256_store_ps(pResults + i/8*32, ymmR2);
//Copy scale values for quat 3 and 2 to all spots in their 128-bit lane
ymmR6 = _mm256_shuffle_ps(scale0, scale0, 0x55);
ymmR7 = _mm256_shuffle_ps(scale1, scale1, 0x55);
//Scale, add, and store results for quats 2 and 3
ymmR0 = _mm256_mul_ps(ymmR6, fromY);
ymmR1 = _mm256_mul_ps(ymmR7, toY);
ymmR2 = _mm256_add_ps(ymmR0, ymmR1);//ymmR2 has all the quat 2 and 3 results
_mm256_store_ps(pResults + i/8*32 + 2*4, ymmR2);
//Copy scale values for quat 5 and 4 to all spots in their 128-bit lane
ymmR6 = _mm256_shuffle_ps(scale0, scale0, 0xaa);
ymmR7 = _mm256_shuffle_ps(scale1, scale1, 0xaa);
//Scale, add, and store results for quats 4 and 5
ymmR0 = _mm256_mul_ps(ymmR6, fromZ);
ymmR1 = _mm256_mul_ps(ymmR7, toZ);
ymmR2 = _mm256_add_ps(ymmR0, ymmR1); //ymmR2 has all the quat 4 and 5 results
_mm256_store_ps(pResults + i/8*32 + 4*4, ymmR2);
//Copy scale values for quat 7 and 6 to all spots in their 128-bit lane
ymmR6 = _mm256_shuffle_ps(scale0, scale0, 0xff);
ymmR7 = _mm256_shuffle_ps(scale1, scale1, 0xff);
//Scale, add, and store results for quats 6 and 7
ymmR0 = _mm256_mul_ps(ymmR6, fromW);
ymmR1 = _mm256_mul_ps(ymmR7, toW);
ymmR2 = _mm256_add_ps(ymmR0, ymmR1); //ymmR2 has all the quat 6 and 7 results
_mm256_store_ps(pResults + i/8*32 + 6*4, ymmR2);
//*****************************************************************
//Unrolled once - repeat the above for another eight quaternions
//Load From-Quat 0 and Quat 1 into one register
fromX = _mm256_load_ps(pFromQuat + i/8*32 + 32);
//Load From-Quat 2 and Quat 3 into one register
fromY = _mm256_load_ps(pFromQuat + i/8*32 + 2*4 + 32);
//Load From-Quat 4 and Quat 5 into one register
fromZ = _mm256_load_ps(pFromQuat + i/8*32 + 4*4 + 32);
//Load From-Quat 6 and Quat 7 into one register
fromW = _mm256_load_ps(pFromQuat + i/8*32 + 6*4 + 32);
//Load To-Quat 0 and Quat 1 into one register
toX = _mm256_load_ps(pToQuat + i/8*32 + 32);
//Load To-Quat 2 and Quat 3 into one register
toY = _mm256_load_ps(pToQuat + i/8*32 + 2*4 + 32);
//Load To-Quat 4 and Quat 5 into one register
toZ = _mm256_load_ps(pToQuat + i/8*32 + 4*4 + 32);
//Load To-Quat 6 and Quat 7 into one register
toW = _mm256_load_ps(pToQuat + i/8*32 + 6*4 + 32);
//*** Compute fromx*tox, fromy*toy, fromz*toz, fromw*tow
ymmR0 = _mm256_mul_ps(fromX, toX); //Quaternion 0 and 1
ymmR1 = _mm256_mul_ps(fromY, toY); //Quaternion 2 and 3
ymmR2 = _mm256_mul_ps(fromZ, toZ); //Quaternion 4 and 5
ymmR3 = _mm256_mul_ps(fromW, toW); //Quaternion 6 and 7
//*** Swizzle to perform adds
//Start collecting terms (step 1 of 2)
//Get y3, y1, x3, x1, y2, y0, x2, x0
ymmR4 = _mm256_unpacklo_ps(ymmR0, ymmR1);
//Get w3, w1, z3, z1, w2, w0, z2, z0
ymmR5 = _mm256_unpackhi_ps(ymmR0, ymmR1);
//Get y7, y5, x7, x5, y6, y4, x6, x4
ymmR6 = _mm256_unpacklo_ps(ymmR2, ymmR3);
//Get w7, w5, z7, z5, w6, w4, z6, z4
ymmR7 = _mm256_unpackhi_ps(ymmR2, ymmR3);
//Finish collecting terms (step 2 of 2)
//Get x7, x5, x3, x1, x6, x4, x2, x0
ymmR0 = _mm256_castpd_ps(_mm256_unpacklo_pd(_mm256_castps_pd(ymmR4), _mm256_castps_pd(ymmR6)));
//Get y7, y5, y3, y1, y6, y4, y2, y0
ymmR1 = _mm256_castpd_ps(_mm256_unpackhi_pd(_mm256_castps_pd(ymmR4), _mm256_castps_pd(ymmR6)));
ymmR4 = _mm256_add_ps(ymmR0, ymmR1);
//Get z7, z5, z3, z1, z6, z4, z2, z0
ymmR2 = _mm256_castpd_ps(_mm256_unpacklo_pd(_mm256_castps_pd(ymmR5), _mm256_castps_pd(ymmR7)));
//Get w7, w5, w3, w1, w6, w4, w2, w0
ymmR3 = _mm256_castpd_ps(_mm256_unpackhi_pd(_mm256_castps_pd(ymmR5), _mm256_castps_pd(ymmR7)));
//Finish adding the terms
ymmR5 = _mm256_add_ps(ymmR2, ymmR3);
cosom = _mm256_add_ps(ymmR4, ymmR5);
//*** Compute the absolute value of above
absCosom = _mm256_and_ps(cosom, clearSignBit);
signBit = _mm256_and_ps(cosom, setSignBit); //Used to invert scale1 later
//*** Compute 1.0 - (above squared)
ymmR0 = _mm256_mul_ps(absCosom, absCosom);
sinsqr = _mm256_sub_ps(allOnes, ymmR0);
//Watch for very small values
ymmR1 = _mm256_xor_ps(ymmR1, ymmR1); //Zeros
ymmR1 = _mm256_cmpeq_ps(ymmR1, sinsqr);
ymmR1 = _mm256_and_ps(ymmR1, tiny); //Make them tiny, not zero
sinsqr = _mm256_and_ps(sinsqr, clearSignBit);//Make them positive
sinsqr = _mm256_or_ps(sinsqr, ymmR1);
//Compute 1/(square root of above)
sinom = _mm256_rsqrt_ps(sinsqr);
ymmR0 = _mm256_mul_ps(sinsqr, sinom);
ymmR0 = _mm256_mul_ps(ymmR0, sinom);
ymmR0 = _mm256_sub_ps(ymmR0, sqrtC0);
ymmR1 = _mm256_mul_ps(sinom, sqrtC1);
ymmR0 = _mm256_mul_ps(ymmR0, ymmR1);
ymmR0 = _mm256_mul_ps(sinsqr, sinom);
//*** Compute the ArcTangent (omega = arctan(sinom*sinsqr, absCosom)
ymmR1 = absCosom;
absCosom = _mm256_min_ps(absCosom, ymmR0);
ymmR0 = _mm256_max_ps(ymmR0, ymmR1);
ymmR1 = _mm256_cmpeq_ps(ymmR1, absCosom);
ymmR2 = _mm256_rcp_ps(ymmR0);
ymmR0 = _mm256_mul_ps(ymmR0, ymmR2);
ymmR0 = _mm256_mul_ps(ymmR0, ymmR2);
ymmR2 = _mm256_add_ps(ymmR2, ymmR2);
ymmR2 = _mm256_sub_ps(ymmR2, ymmR0);
absCosom = _mm256_mul_ps(absCosom, ymmR2);
ymmR0 = ymmR1; //copy the mask
ymmR0 = _mm256_and_ps(ymmR0, setSignBit);
absCosom = _mm256_xor_ps(absCosom, ymmR0);
//cmp mask determines contents: Pi/2 or 0.0
ymmR1 = _mm256_and_ps(ymmR1, halfPi);
ymmR0 = _mm256_mul_ps(absCosom, absCosom);
ymmR2 = _mm256_mul_ps(atanC0, ymmR0);
ymmR2 = _mm256_add_ps(ymmR2, atanC1);
ymmR2 = _mm256_mul_ps(ymmR2, ymmR0);
ymmR2 = _mm256_add_ps(ymmR2, atanC2);
ymmR2 = _mm256_mul_ps(ymmR2, ymmR0);
ymmR2 = _mm256_add_ps(ymmR2, atanC3);
ymmR2 = _mm256_mul_ps(ymmR2, ymmR0);
ymmR2 = _mm256_add_ps(ymmR2, atanC4);
ymmR2 = _mm256_mul_ps(ymmR2, ymmR0);
ymmR2 = _mm256_add_ps(ymmR2, atanC5);
ymmR2 = _mm256_mul_ps(ymmR2, ymmR0);
ymmR2 = _mm256_add_ps(ymmR2, atanC6);
ymmR2 = _mm256_mul_ps(ymmR2, ymmR0);
ymmR2 = _mm256_add_ps(ymmR2, atanC7);
ymmR2 = _mm256_mul_ps(ymmR2, ymmR0);
ymmR2 = _mm256_add_ps(ymmR2, allOnes);
ymmR2 = _mm256_mul_ps(ymmR2, absCosom);
omega = _mm256_add_ps(ymmR2, ymmR1);
//*** Compute the first scale factor
//Compute [1.0 - (move factor)]*above?
ymmR1 = _mm256_mul_ps(factor, omega);
ymmR0 = _mm256_sub_ps(omega, ymmR1);
//Compute both scale factors
//Compute sin(above)
ymmR1 = ymmR0; //used to calculate scale0
//Compute factor*omega
ymmR6 = _mm256_mul_ps(factor, omega);
ymmR4 = ymmR6; //used to calculate scale1
ymmR1 = _mm256_mul_ps(ymmR1, ymmR1);
ymmR4 = _mm256_mul_ps(ymmR4, ymmR4); //scale1
ymmR2 = _mm256_mul_ps(sinC0, ymmR1);
ymmR5 = _mm256_mul_ps(sinC0, ymmR4); //scale1
ymmR2 = _mm256_add_ps(ymmR2, sinC1);
ymmR2 = _mm256_mul_ps(ymmR2, ymmR1);
ymmR5 = _mm256_add_ps(ymmR5, sinC1); //scale1
ymmR5 = _mm256_mul_ps(ymmR5, ymmR4); //scale1
ymmR2 = _mm256_add_ps(ymmR2, sinC2);
ymmR2 = _mm256_mul_ps(ymmR2, ymmR1);
ymmR5 = _mm256_add_ps(ymmR5, sinC2); //scale1
ymmR5 = _mm256_mul_ps(ymmR5, ymmR4); //scale1
ymmR2 = _mm256_add_ps(ymmR2, sinC3);
ymmR2 = _mm256_mul_ps(ymmR2, ymmR1);
ymmR5 = _mm256_add_ps(ymmR5, sinC3); //scale1
ymmR5 = _mm256_mul_ps(ymmR5, ymmR4); //scale1
ymmR2 = _mm256_add_ps(ymmR2, sinC4);
ymmR2 = _mm256_mul_ps(ymmR2, ymmR1);
ymmR5 = _mm256_add_ps(ymmR5, sinC4); //scale1
ymmR5 = _mm256_mul_ps(ymmR5, ymmR4); //scale1
ymmR2 = _mm256_add_ps(ymmR2, allOnes);
ymmR2 = _mm256_mul_ps(ymmR2, ymmR0); //ymmR2 has the sin(x) for eight
ymmR5 = _mm256_add_ps(ymmR5, allOnes); //scale1
ymmR5 = _mm256_mul_ps(ymmR5, ymmR6); //ymmR5 has the sin(x) for eight
//Compute above*sinom
scale0 = _mm256_mul_ps(ymmR2, sinom); //scale0 has the first scale factor
scale1 = _mm256_mul_ps(ymmR5, sinom); //scale1 has the second scale factor
//*** invert the second scale factor if
//*** that first sum of products is negative
scale1 = _mm256_xor_ps(scale1, signBit);
//*** Compute the final results by scaling, adding, then storing
ymmR6 = _mm256_shuffle_ps(scale0, scale0, 0x00);
ymmR7 = _mm256_shuffle_ps(scale1, scale1, 0x00);
ymmR0 = _mm256_mul_ps(ymmR6, fromX);
ymmR1 = _mm256_mul_ps(ymmR7, toX);
ymmR2 = _mm256_add_ps(ymmR0, ymmR1); //ymmR2 has all the quat 0 and 1 results
_mm256_store_ps(pResults + i/8*32 + 32, ymmR2);
ymmR6 = _mm256_shuffle_ps(scale0, scale0, 0x55);
ymmR7 = _mm256_shuffle_ps(scale1, scale1, 0x55);
ymmR0 = _mm256_mul_ps(ymmR6, fromY);
ymmR1 = _mm256_mul_ps(ymmR7, toY);
ymmR2 = _mm256_add_ps(ymmR0, ymmR1); //ymmR2 has all the quat 2 and 3 results
_mm256_store_ps(pResults + i/8*32 + 2*4 + 32, ymmR2);
ymmR6 = _mm256_shuffle_ps(scale0, scale0, 0xaa);
ymmR7 = _mm256_shuffle_ps(scale1, scale1, 0xaa);
ymmR0 = _mm256_mul_ps(ymmR6, fromZ);
ymmR1 = _mm256_mul_ps(ymmR7, toZ);
ymmR2 = _mm256_add_ps(ymmR0, ymmR1); //ymmR2 has all the quat 4 and 5 results
_mm256_store_ps(pResults + i/8*32 + 4*4 + 32, ymmR2);
ymmR6 = _mm256_shuffle_ps(scale0, scale0, 0xff);
ymmR7 = _mm256_shuffle_ps(scale1, scale1, 0xff);
ymmR0 = _mm256_mul_ps(ymmR6, fromW);
ymmR1 = _mm256_mul_ps(ymmR7, toW);
ymmR2 = _mm256_add_ps(ymmR0, ymmR1); //ymmR2 has all the quat 6 and 7 results
_mm256_store_ps(pResults + i/8*32 + 6*4 + 32, ymmR2);
}
//Handle any remaining quaternions
//Operate on all the quaternions
{
float cosom, absCosom, sinom, sinSqr, omega, scale0, scale1;
for(int i = mod16QuaternionCount; i < g_quaternionCount; i++) {
cosom = fromQuaternion[i].x*toQuaternion[i].x + fromQuaternion[i].y*toQuaternion[i].y + fromQuaternion[i].z*toQuaternion[i].z + fromQuaternion[i].w*toQuaternion[i].w;
absCosom = fabs(cosom);
if((1.0f - absCosom) > 1e-6f) {
sinSqr = 1.0f - absCosom*absCosom;
sinom = reciprocalSqrt(sinSqr);
omega = atanPositive(sinSqr*sinom, absCosom, i);
scale0 = sinZeroHalfPi((1.0f - g_factor) * omega) * sinom;
scale1 = sinZeroHalfPi(g_factor * omega) * sinom;
}
else {
scale0 = 1.0f - g_factor;
scale1 = g_factor;
}
scale1 = (cosom >= 0.0f) ? scale1 : -scale1;
resultQuaternion[i].x = scale0 * fromQuaternion[i].x + scale1 * toQuaternion[i].x;
resultQuaternion[i].y = scale0 * fromQuaternion[i].y + scale1 * toQuaternion[i].y;
resultQuaternion[i].z = scale0 * fromQuaternion[i].z + scale1 * toQuaternion[i].z;
resultQuaternion[i].w = scale0 * fromQuaternion[i].w + scale1 * toQuaternion[i].w;
}
}
}
}
参考文献
この記事では、以下の文献を参照しています。これらの文献には、この記事で説明している内容を理解するための背景情報が記述されています。
1. J.M.P.van Waveren, Slerping Clock Cycles, Id Software, Inc. 2005
2. J.M.P.van Waveren, From Quaternions to Matrix and Back, Id Software, Inc. 2005
3. Ken Shoemake, Animating Rotation with Quaternion Curves, Computer Graphics 19(3): 24-254, 1985, http://portal.acm.org/citation.cfm?doid=325334.325242
著者紹介
Pallavi Mehrotra – Motorola 社で CDMA Network のソフトウェア開発を経て、2006 年にシニア・ソフトウェア・エンジニアとしてインテルに入社。現在、SSG Apple 推進チームのメンバーとして、電力効率とパフォーマンスを向上するべく Mac OS* X アプリケーションの最適化に取り組んでいます。アリゾナ州立大学でコンピューター・サイエンスの修士号を、インドで電気工学の学士号を取得しています。
Richard Hubbard – シニア・ソフトウェア・エンジニア。SSG Apple 推進チームのメンバーとして、電力効率とパフォーマンスを向上するべく Mac OS* X アプリケーションの最適化に取り組んでいます。スティーブンス工科大学で電気工学の修士号を、ニュージャージー工科大学でコンピューター工学の学士号を取得しています。
編集部追加
本記事においては intrinsic やプログラミングによる最適化の効果を紹介していますが、インテル® C++/Fortran コンパイラーの最適化、および自動ベクトル化の機能もバージョンアップを重ねてより洗練されています。是非とも1度、最新版にてコンパイルをお試しいただければ幸いです。また、性能が上がらない場合には詳細をお知らせください。インテル® C++/Fortran Composer XE 評価版のダウンロード、お問い合わせはエクセルソフト株式会社まで。
なお本記事のサンプルコードは、インテル® C++ コンパイラー 12.0/12.1 ではコンパイルエラーになります。お試しになりたい場合には、バージョン 11.0/11.1 をご利用ください。最新版のコンパイラーを評価中、あるいは製品ライセンスをお持ちであれば、旧バージョンのコンパイラーもご利用いただけます。


