この記事は、インテル® ソフトウェア・ネットワークに掲載されている「Benefits of Intel® AVX For Small Matrices」(http://software.intel.com/en-us/articles/benefits-of-intel-avx-for-small-matrices/) の日本語参考訳です。
はじめに
インテル® アドバンスト・ベクトル・エクステンション (インテル® AVX) は、特に浮動小数点データのロードとストアおよび演算において、インテル® ストリーミング SIMD 拡張命令 (インテル® SSE) の機能を拡張します。インテル® AVX における YMM レジスターは、現在の XMM レジスターの 2 倍の幅があり、より広いデータ幅で演算を行うことができます。以前の 128 ビットの SIMD 命令セットの拡張と比べて電力効率に優れており、浮動小数点のパフォーマンス密度を向上させます。
ここでは、これまでよりも広い 256 ビット・レジスター、新しいデータ操作、演算プリミティブなどのインテル® AVX アーキテクチャーの機能が、小行列の演算にどのような利点をもたらすかを検証します。この記事では、行列の加算や乗算などの単純な演算から、行列式の計算などのより複雑な演算まで取り上げます。
シミュレーション環境
ここで行われたパフォーマンス向上の検証は、インテルのパフォーマンス・シミュレーター・コード Sandy Bridge (開発コード名) に基づいています。そのため、テストデータはすでにキャッシュにあると仮定します。パフォーマンスは、C 組み込み関数を利用して記述したコードを同じシミュレーター Sandy Bridge (開発コード名) で実行した場合のインテル® AVX と、対応するインテル® SSE 実装の相対パフォーマンスを示しています。コードはインテル® C コンパイラー 11.0.074 (未公開バージョン) でコンパイルされています。
最初に、行列の加算について見てみましょう。
行列の加算
2 つの行列 A と B があり、ともに [I x J] の場合、行列の加算は次の式で定義されます。
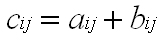
各 Cij の結果は、対応する行列の要素の合計によって計算されます。
このアルゴリズムは、_mm256_load_ps 組み込み関数を使用して、各入力行列から 8 つの単精度浮動小数点数をロードします。そして、_mm256_add_ps 組み込み関数を使用して、8 要素の合計を並列に計算します。8 つの結果は、_mm256_store_ps 組み込み関数を使用して、出力行列に書き込まれます。新しい 256 ビットのインテル® AVX 拡張の使用することで、4 つではなく、8 つの単精度浮動小数点数のロード、加算、ストア命令を並列に実行できるため、128 ビット・アーキテクチャーと比べてバンド幅が倍増します。
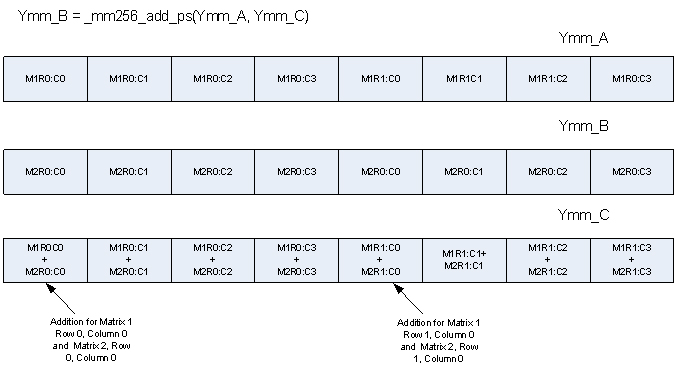
図 1 – 2 つの 4×4 行列の加算
行列の加算のソースコードは、このドキュメントの「ソースコード」セクションを参照してください。
次に、行列の乗算について見てみましょう。
行列の乗算
2 つの行列 A と B があり、A は [I x N]、B は [N x J] の場合、行列の乗算は次の式で定義されます。
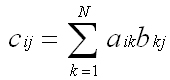
各 Cij の結果は、行列 A の各行と行列 B の列のドット積によって計算されます。
2 つの 8×8 行列の場合、アルゴリズムは一連の並列処理により 1 つの出力行のすべての結果を計算します。行列の乗算では、行列 A の行の各要素に対応する行列 B の各列の要素を掛ける必要があるため、8 回実行される要素単位の乗算で行列 A の同じ要素がオペランドの 1 つとして使用されます。この行列 A の要素を YMM レジスターのすべての場所にコピーすることで、パフォーマンスを向上できます。_mm256_broadcast_ss 組み込み関数は、レジスターに含まれる 8 つの単精度浮動小数点数すべてに 1 つの要素をブロードキャスト (コピー) します。
最初に一連の 8 つの _mm256_load_ps 組み込み関数を使用して、行列 B の各行を読み取ります。そして、_mm256_broadcast_ss を使用して、行列 A の行の 1 つの要素を YMM レジスターのすべての場所にコピーします。この方法で、行列 A のこの行の各要素が YMM レジスターにコピーされます。
行列 A のブロードキャストされた要素に行列 B の行を掛けて、その結果を合計することによって、8 要素のドット積が並列に計算されます。そのためには、ブロードキャストされた a11 と行列 B の 1 行目をオペランドとして、_mm256_mul_ps を実行します。そして、ブロードキャストされた a12 と行列 B の 2 行目をオペランドとして、乗算を繰り返します。_mm256_add_ps を使用して、この 2 つの乗算の結果を足して部分和が求められます。同じ処理を a13 と行列 B の 3 行目、a14 と行列 B の 4 行目に対しても行います。残りの要素と行の部分和が計算されます。次に 4 要素の部分和を足して、その結果を出力行列 C に格納し、この行のドット積計算を終了します。
この処理を、行列 A の異なる行を使用してあと 7 回繰り返し、行列の乗算を完了します。
行列の加算と乗算は、単純で基本的なビルディング・ブロックです。次のセクションでは、多くのアプリケーションで使用されている重要な行列演算の 1 つである行列式の評価について見てみましょう。
行列式
行列式は、連立一次方程式を分析する場合に非常に便利です。行列式を計算するためのアルゴリズムはいくつかあります。ここで説明する方法は、次の式によって定義された小行列のラプラス展開です。
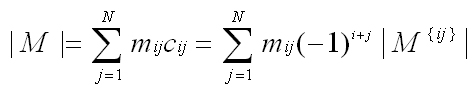
上記の式において、行列式を簡単に計算することができる 2×2 行列になるまで、より小さなサイズの小行列に対してアルゴリズムが再帰的に繰り返されます。
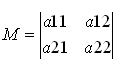
図 7 – 2×2 行列
2×2 行列の行列式は、次のように定義されます。
![]()
4×4 行列 M の場合:

図 3 – 4×4 行列
ラプラス方程式は、次のように展開されます。

式 1 – 4×4 行列の行列式
インテル® AVX は、展開された式 (式 1) を使用し、並列 SIMD アーキテクチャーを最大限に活用して、8 つの行列の行列式を同時に計算することで最高のスループットを実現します。アルゴリズムは 2 つのステップから成るプロセスとして実装されます。
最初に、8 つの行列からそれぞれ最初の 2 行を読み取り、置き替え (転置操作に似ている)、対応する各行列の要素を 8 つの YMM レジスターに収集します。その後、次の 2 行を読み取り、置き替えます。
要素が収集されると、8 つの行列の行列式の計算を並列に実行できます。すべての算術関数が完了すると、8 つの行列式の値は 1 つの YMM レジスターに格納され、出力に格納されます。次のコードは、小行列の要素 a11 の行列式を計算します。同様に、展開された式に応じて、要素 a12、a13、a14 が計算されます。
// 8 つの行列の a11a22(a33a44 - a43a34) を計算 ymm_a11a22 = _mm256_mul_ps(ymm_a11, ymm_a22); ymm_a33a44 = _mm256_mul_ps(ymm_a33, ymm_a44); ymm_a43a34 = _mm256_mul_ps(ymm_a43, ymm_a34); ymm_a33a44_a43a34 = _mm256_sub_ps(ymm_a33a44, ymm_a43a34); ymm_a11a22_D = _mm256_mul_ps(ymm_a11a22, ymm_a33a44_a43a34); // 8 つの行列の a11a23(a32a44 - a34a42) を計算 ymm_a11a23 = _mm256_mul_ps(ymm_a11, ymm_a23); ymm_a32a44 = _mm256_mul_ps(ymm_a32, ymm_a44); ymm_a34a42 = _mm256_mul_ps(ymm_a34, ymm_a42); ymm_a32a44_a34a42 = _mm256_sub_ps(ymm_a32a44, ymm_a34a42); ymm_a11a23_D = _mm256_mul_ps(ymm_a11a23, ymm_a32a44_a34a42); // 8 つの行列の a11a24(a32a43 - a42a33) を計算 ymm_a11a24 = _mm256_mul_ps(ymm_a11, ymm_a24); ymm_a32a43 = _mm256_mul_ps(ymm_a32, ymm_a43); ymm_a42a33 = _mm256_mul_ps(ymm_a42, ymm_a33); ymm_a32a43_a42a33 = _mm256_sub_ps(ymm_a32a43, ymm_a42a33); ymm_a11a24_D = _mm256_mul_ps(ymm_a11a24, ymm_a32a43_a42a33); // 部分行列式の計算: (a11a22(a33a44 - a43a34) + // 8 つの行列の a11a23(a32a44 - a34a42) + a11a24(a32a43 - a42a33)) を計算 ymm_a11a22_D = mm256_sub_ps(ymm_a11a22_D, ymm_a11a23_D); ymm_a11_D = _mm256_add_ps(ymm_a11a22_D, ymm_a11a24_D);
最後に、a11、a12、a13、a14 の部分行列式が加算され、最終の行列式の値が得られます。スループットを最大にするため、これらの計算はそれぞれ、8 つの行列を同時に処理します。
// 最終の行列式の値の計算: // a11、a12、a13、a14 の行列式を加算 ymm_a11_D = _mm256_add_ps(ymm_a11_D, ymm_a12_D); ymm_a13_D = _mm256_add_ps(ymm_a13_D, ymm_a14_D); ymm_a11_D = _mm256_add_ps(ymm_a11_D, ymm_a13_D);
結果
128 ビットのコードと対応する 256 ビットのコードの両方をインテル® AVX パフォーマンス・シミュレーターで実行したところ、次のような結果が得られました。
表 1 – 256 ビットのコードと 128 ビットのコードを比べたスピードアップ
| アルゴリズム | スピードアップ | パラメーター |
| 行列の加算 | 1.8 倍 | 4×4 行列 |
| 乗算を使用した行列の乗算 | 1.77 倍 | 8×8 行列 |
| 行列式 | 1.56 倍 | 4×4 行列 |
まとめ
8×8 行列の乗算アルゴリズムと 16×16 行列の加算アルゴリズムの両方で、それぞれ 1.77 倍と 1.8 倍となり、インテル® AVX バージョンのほうがインテル® SSE よりも優れた結果となりました。これは、インテル® AVX のほうが、レジスターの幅を活用することで 1 命令あたり 2 倍のオペランドを処理し、インテル® SSE よりも高いスループットを達成できることを示した良い例です。
行列式アルゴリズムでは、8 つの行列の行列式の計算を同時に実行することでパフォーマンスが向上しました。ただし、行列式の計算の前の 2 つの 8×8 転置により、パフォーマンスはやや制限されます。
一般に、アプリケーションはメモリー集約型よりも計算集約型のほうが、より優れたパフォーマンス・スピードアップが得られます。
ソースコード
完全なソースコードは http://software.intel.com/file/23397 からダウンロードできます。
部分的なソースコードは、以下のセクションにリストされています。
行列の加算アルゴリズム
// 次のコードは、単精度浮動小数点値の 2 つの 4×4 行列の加算を行い、その結果を別の 4×4 行列に格納します。
int iBufferHeight = miMatrixWidth; // 行列の行数
int iBufferWidth = miMatrixHeight; // 行列の列数
// 入力バッファー 1 と 2 を 2 つの入力行列に初期化し、
// 出力バッファーを最終結果を格納するための 3 つ目の行列に初期化
float* pImage1 = InputBuffer1;
float* pImage2 = InputBuffer2;
float* pOutImage = OutputBuffer;
for(int iY = 0; iY < iBufferHeight; iY+= 2)
{
// 入力行列 1 と 2 から 8 つの単精度浮動小数点数をロード
__m256 Ymm_A = _mm256_load_ps(pImage1);
__m256 Ymm_C = _mm256_load_ps(pImage2);
// 8 つの単精度浮動小数点数を並列に加算
__m256 Ymm_B = _mm256_add_ps (Ymm_A, Ymm_C);
// 8 つの加算結果を出力行列に格納
_mm256_store_ps(pOutImage, Ymm_B);
// 入力バッファーと出力バッファーを進める
pOutImage+=8;
pImage1+=8;
pImage2+=8;
}
行列の乗算アルゴリズム
// 次のコードは、単精度浮動小数点値の 2 つの 8x8 行列の乗算を行います。
__m256 ymm0, ymm1, ymm2, ymm3, ymm4, ymm5, ymm6, ymm7, ymm8, ymm9, ymm10, ymm11, ymm12, ymm13, ymm14, ymm15; // ポインターを初期化 float * pMatrix2 = InputBuffer2; float * pIn = InputBuffer1; float * pOut = OutputBuffer; // 行列 B の 8 つの行を ymm レジスターに読み込む ymm8 = _mm256_load_ps((float *) (pMatrix2)); ymm9 = _mm256_load_ps((float *) (pMatrix2 + 1*8)); ymm10 = _mm256_load_ps((float *) (pMatrix2 + 2*8)); ymm11 = _mm256_load_ps((float *) (pMatrix2 + 3*8)); ymm12 = _mm256_load_ps((float *) (pMatrix2 + 4*8)); ymm13 = _mm256_load_ps((float *) (pMatrix2 + 5*8)); ymm14 = _mm256_load_ps((float *) (pMatrix2 + 6*8)); ymm15 = _mm256_load_ps((float *) (pMatrix2 + 7*8)); // 行列 A の行 1 の各要素を ymm レジスターにブロードキャスト ymm0 = _mm256_broadcast_ss(pIn); ymm1 = _mm256_broadcast_ss(pIn + 1); ymm2 = _mm256_broadcast_ss(pIn + 2); ymm3 = _mm256_broadcast_ss(pIn + 3); ymm4 = _mm256_broadcast_ss(pIn + 4); ymm5 = _mm256_broadcast_ss(pIn + 5); ymm6 = _mm256_broadcast_ss(pIn + 6); ymm7 = _mm256_broadcast_ss(pIn + 7); // A11 と行列 B の行 1 を掛ける ymm0 = _mm256_mul_ps(ymm0, ymm8); // A12 と行列 B の行 2 を掛ける ymm1 = _mm256_mul_ps(ymm1, ymm9); // 最初の部分和を計算 ymm0 = _mm256_add_ps(ymm0, ymm1); // A13、A14 と行列 B の 行 3、行 4 で同じ処理を実行 ymm2 = _mm256_mul_ps(ymm2, ymm10); ymm3 = _mm256_mul_ps(ymm3, ymm11); ymm2 = _mm256_add_ps(ymm2, ymm3); // A15、A16 と行列 B の 行 5、行 6 で同じ処理を実行 ymm4 = _mm256_mul_ps(ymm4, ymm12); ymm5 = _mm256_mul_ps(ymm5, ymm13); ymm4 = _mm256_add_ps(ymm4, ymm5); // A17、A18 と行列 B の 行 7、行 8 で同じ処理を実行 ymm6 = _mm256_mul_ps(ymm6, ymm14); ymm7 = _mm256_mul_ps(ymm7, ymm15); ymm6 = _mm256_add_ps(ymm6, ymm7); // 最後の 3 つの加算を実行 ymm0 = _mm256_add_ps(ymm0, ymm2); ymm4 = _mm256_add_ps(ymm4, ymm6); ymm0 = _mm256_add_ps(ymm0, ymm4); // 行列 C の行 1 に結果を格納 _mm256_store_ps((float *) (pOut), ymm0); // 行列 A の行 2 で処理を繰り返す ymm0 = _mm256_broadcast_ss(pIn + 1*8); ymm1 = _mm256_broadcast_ss(pIn + 1*8 + 1); ymm2 = _mm256_broadcast_ss(pIn + 1*8 + 2); ymm3 = _mm256_broadcast_ss(pIn + 1*8 + 3); ymm4 = _mm256_broadcast_ss(pIn + 1*8 + 4); ymm5 = _mm256_broadcast_ss(pIn + 1*8 + 5); ymm6 = _mm256_broadcast_ss(pIn + 1*8 + 6); ymm7 = _mm256_broadcast_ss(pIn + 1*8 + 7); ymm0 = _mm256_mul_ps(ymm0, ymm8); ymm1 = _mm256_mul_ps(ymm1, ymm9); ymm0 = _mm256_add_ps(ymm0, ymm1); ymm2 = _mm256_mul_ps(ymm2, ymm10); ymm3 = _mm256_mul_ps(ymm3, ymm11); ymm2 = _mm256_add_ps(ymm2, ymm3); ymm4 = _mm256_mul_ps(ymm4, ymm12); ymm5 = _mm256_mul_ps(ymm5, ymm13); ymm4 = _mm256_add_ps(ymm4, ymm5); ymm6 = _mm256_mul_ps(ymm6, ymm14); ymm7 = _mm256_mul_ps(ymm7, ymm15); ymm6 = _mm256_add_ps(ymm6, ymm7); ymm0 = _mm256_add_ps(ymm0, ymm2); ymm4 = _mm256_add_ps(ymm4, ymm6); ymm0 = _mm256_add_ps(ymm0, ymm4); _mm256_store_ps((float *) (pOut + 1*8), ymm0); // 行列 A の行 3 で処理を繰り返す ymm0 = _mm256_broadcast_ss(pIn + 2*8); ymm1 = _mm256_broadcast_ss(pIn + 2*8 + 1); ymm2 = _mm256_broadcast_ss(pIn + 2*8 + 2); ymm3 = _mm256_broadcast_ss(pIn + 2*8 + 3); ymm4 = _mm256_broadcast_ss(pIn + 2*8 + 4); ymm5 = _mm256_broadcast_ss(pIn + 2*8 + 5); ymm6 = _mm256_broadcast_ss(pIn + 2*8 + 6); ymm7 = _mm256_broadcast_ss(pIn + 2*8 + 7); ymm0 = _mm256_mul_ps(ymm0, ymm8); ymm1 = _mm256_mul_ps(ymm1, ymm9); ymm0 = _mm256_add_ps(ymm0, ymm1); ymm2 = _mm256_mul_ps(ymm2, ymm10); ymm3 = _mm256_mul_ps(ymm3, ymm11); ymm2 = _mm256_add_ps(ymm2, ymm3); ymm4 = _mm256_mul_ps(ymm4, ymm12); ymm5 = _mm256_mul_ps(ymm5, ymm13); ymm4 = _mm256_add_ps(ymm4, ymm5); ymm6 = _mm256_mul_ps(ymm6, ymm14); ymm7 = _mm256_mul_ps(ymm7, ymm15); ymm6 = _mm256_add_ps(ymm6, ymm7); ymm0 = _mm256_add_ps(ymm0, ymm2); ymm4 = _mm256_add_ps(ymm4, ymm6); ymm0 = _mm256_add_ps(ymm0, ymm4); _mm256_store_ps((float *) (pOut + 2*8), ymm0); // 行列 A の行 4 で処理を繰り返す ymm0 = _mm256_broadcast_ss(pIn + 3*8); ymm1 = _mm256_broadcast_ss(pIn + 3*8 + 1); ymm2 = _mm256_broadcast_ss(pIn + 3*8 + 2); ymm3 = _mm256_broadcast_ss(pIn + 3*8 + 3); ymm4 = _mm256_broadcast_ss(pIn + 3*8 + 4); ymm5 = _mm256_broadcast_ss(pIn + 3*8 + 5); ymm6 = _mm256_broadcast_ss(pIn + 3*8 + 6); ymm7 = _mm256_broadcast_ss(pIn + 3*8 + 7); ymm0 = _mm256_mul_ps(ymm0, ymm8); ymm1 = _mm256_mul_ps(ymm1, ymm9); ymm0 = _mm256_add_ps(ymm0, ymm1); ymm2 = _mm256_mul_ps(ymm2, ymm10); ymm3 = _mm256_mul_ps(ymm3, ymm11); ymm2 = _mm256_add_ps(ymm2, ymm3); ymm4 = _mm256_mul_ps(ymm4, ymm12); ymm5 = _mm256_mul_ps(ymm5, ymm13); ymm4 = _mm256_add_ps(ymm4, ymm5); ymm6 = _mm256_mul_ps(ymm6, ymm14); ymm7 = _mm256_mul_ps(ymm7, ymm15); ymm6 = _mm256_add_ps(ymm6, ymm7); ymm0 = _mm256_add_ps(ymm0, ymm2); ymm4 = _mm256_add_ps(ymm4, ymm6); ymm0 = _mm256_add_ps(ymm0, ymm4); _mm256_store_ps((float *) (pOut + 3*8), ymm0); // 行列 A の行 5 で処理を繰り返す ymm0 = _mm256_broadcast_ss(pIn + 4*8); ymm1 = _mm256_broadcast_ss(pIn + 4*8 + 1); ymm2 = _mm256_broadcast_ss(pIn + 4*8 + 2); ymm3 = _mm256_broadcast_ss(pIn + 4*8 + 3); ymm4 = _mm256_broadcast_ss(pIn + 4*8 + 4); ymm5 = _mm256_broadcast_ss(pIn + 4*8 + 5); ymm6 = _mm256_broadcast_ss(pIn + 4*8 + 6); ymm7 = _mm256_broadcast_ss(pIn + 4*8 + 7); ymm0 = _mm256_mul_ps(ymm0, ymm8); ymm1 = _mm256_mul_ps(ymm1, ymm9); ymm0 = _mm256_add_ps(ymm0, ymm1); ymm2 = _mm256_mul_ps(ymm2, ymm10); ymm3 = _mm256_mul_ps(ymm3, ymm11); ymm2 = _mm256_add_ps(ymm2, ymm3); ymm4 = _mm256_mul_ps(ymm4, ymm12); ymm5 = _mm256_mul_ps(ymm5, ymm13); ymm4 = _mm256_add_ps(ymm4, ymm5); ymm6 = _mm256_mul_ps(ymm6, ymm14); ymm7 = _mm256_mul_ps(ymm7, ymm15); ymm6 = _mm256_add_ps(ymm6, ymm7); ymm0 = _mm256_add_ps(ymm0, ymm2); ymm4 = _mm256_add_ps(ymm4, ymm6); ymm0 = _mm256_add_ps(ymm0, ymm4); _mm256_store_ps((float *) (pOut + 4*8), ymm0); // 行列 A の行 6 で処理を繰り返す ymm0 = _mm256_broadcast_ss(pIn + 5*8); ymm1 = _mm256_broadcast_ss(pIn + 5*8 + 1); ymm2 = _mm256_broadcast_ss(pIn + 5*8 + 2); ymm3 = _mm256_broadcast_ss(pIn + 5*8 + 3); ymm4 = _mm256_broadcast_ss(pIn + 5*8 + 4); ymm5 = _mm256_broadcast_ss(pIn + 5*8 + 5); ymm6 = _mm256_broadcast_ss(pIn + 5*8 + 6); ymm7 = _mm256_broadcast_ss(pIn + 5*8 + 7); ymm0 = _mm256_mul_ps(ymm0, ymm8); ymm1 = _mm256_mul_ps(ymm1, ymm9); ymm0 = _mm256_add_ps(ymm0, ymm1); ymm2 = _mm256_mul_ps(ymm2, ymm10); ymm3 = _mm256_mul_ps(ymm3, ymm11); ymm2 = _mm256_add_ps(ymm2, ymm3); ymm4 = _mm256_mul_ps(ymm4, ymm12); ymm5 = _mm256_mul_ps(ymm5, ymm13); ymm4 = _mm256_add_ps(ymm4, ymm5); ymm6 = _mm256_mul_ps(ymm6, ymm14); ymm7 = _mm256_mul_ps(ymm7, ymm15); ymm6 = _mm256_add_ps(ymm6, ymm7); ymm0 = _mm256_add_ps(ymm0, ymm2); ymm4 = _mm256_add_ps(ymm4, ymm6); ymm0 = _mm256_add_ps(ymm0, ymm4); _mm256_store_ps((float *) (pOut + 5*8), ymm0); // 行列 A の行 7 で処理を繰り返す ymm0 = _mm256_broadcast_ss(pIn + 6*8); ymm1 = _mm256_broadcast_ss(pIn + 6*8 + 1); ymm2 = _mm256_broadcast_ss(pIn + 6*8 + 2); ymm3 = _mm256_broadcast_ss(pIn + 6*8 + 3); ymm4 = _mm256_broadcast_ss(pIn + 6*8 + 4); ymm5 = _mm256_broadcast_ss(pIn + 6*8 + 5); ymm6 = _mm256_broadcast_ss(pIn + 6*8 + 6); ymm7 = _mm256_broadcast_ss(pIn + 6*8 + 7); ymm0 = _mm256_mul_ps(ymm0, ymm8); ymm1 = _mm256_mul_ps(ymm1, ymm9); ymm0 = _mm256_add_ps(ymm0, ymm1); ymm2 = _mm256_mul_ps(ymm2, ymm10); ymm3 = _mm256_mul_ps(ymm3, ymm11); ymm2 = _mm256_add_ps(ymm2, ymm3); ymm4 = _mm256_mul_ps(ymm4, ymm12); ymm5 = _mm256_mul_ps(ymm5, ymm13); ymm4 = _mm256_add_ps(ymm4, ymm5); ymm6 = _mm256_mul_ps(ymm6, ymm14); ymm7 = _mm256_mul_ps(ymm7, ymm15); ymm6 = _mm256_add_ps(ymm6, ymm7); ymm0 = _mm256_add_ps(ymm0, ymm2); ymm4 = _mm256_add_ps(ymm4, ymm6); ymm0 = _mm256_add_ps(ymm0, ymm4); _mm256_store_ps((float *) (pOut + 6*8), ymm0); // 行列 A の行 8 で処理を繰り返す ymm0 = _mm256_broadcast_ss(pIn + 7*8); ymm1 = _mm256_broadcast_ss(pIn + 7*8 + 1); ymm2 = _mm256_broadcast_ss(pIn + 7*8 + 2); ymm3 = _mm256_broadcast_ss(pIn + 7*8 + 3); ymm4 = _mm256_broadcast_ss(pIn + 7*8 + 4); ymm5 = _mm256_broadcast_ss(pIn + 7*8 + 5); ymm6 = _mm256_broadcast_ss(pIn + 7*8 + 6); ymm7 = _mm256_broadcast_ss(pIn + 7*8 + 7); ymm0 = _mm256_mul_ps(ymm0, ymm8); ymm1 = _mm256_mul_ps(ymm1, ymm9); ymm0 = _mm256_add_ps(ymm0, ymm1); ymm2 = _mm256_mul_ps(ymm2, ymm10); ymm3 = _mm256_mul_ps(ymm3, ymm11); ymm2 = _mm256_add_ps(ymm2, ymm3); ymm4 = _mm256_mul_ps(ymm4, ymm12); ymm5 = _mm256_mul_ps(ymm5, ymm13); ymm4 = _mm256_add_ps(ymm4, ymm5); ymm6 = _mm256_mul_ps(ymm6, ymm14); ymm7 = _mm256_mul_ps(ymm7, ymm15); ymm6 = _mm256_add_ps(ymm6, ymm7); ymm0 = _mm256_add_ps(ymm0, ymm2); ymm4 = _mm256_add_ps(ymm4, ymm6); ymm0 = _mm256_add_ps(ymm0, ymm4); _mm256_store_ps((float *) (pOut + 7*8), ymm0);
行列の行列式
// 次のコードは、単精度浮動小数点値の 8 つの 4x4 行列の行列式の値を並列に計算します。
#define MAT_WIDTH 4
#define MAT_SIZE 12
__m256 ymm_a11, ymm_a12, ymm_a13, ymm_a14;
__m256 ymm_a21, ymm_a22, ymm_a23, ymm_a24;
__m256 ymm_a31, ymm_a32, ymm_a33, ymm_a34;
__m256 ymm_a41, ymm_a42, ymm_a43, ymm_a44;
__m256 ymm0, ymm1, ymm2, ymm3, ymm4, ymm5, ymm6, ymm7;
__m256 ymma, ymmb, ymmc, ymmd, ymme, ymmf, ymmg, ymmh;
float * pIn = (float *) InputBuffer;
float * pOut = (float *) OutputBuffer;
for (unsigned int k = 0; k < lc; k++)
{
// 8 つの 4x4 行列の最初の 2 行の浮動小数点数を
// ymm レジスターに読み込み
ymm0 = _mm256_load_ps((float *) (pIn + (0*MAT_SIZE))); // 行列 1
ymm1 = _mm256_load_ps((float *) (pIn + (1*MAT_SIZE))); // 行列 2
ymm2 = _mm256_load_ps((float *) (pIn + (2*MAT_SIZE))); // 行列 3
ymm3 = _mm256_load_ps((float *) (pIn + (3*MAT_SIZE))); // 行列 4
ymm4 = _mm256_load_ps((float *) (pIn + (4*MAT_SIZE))); // 行列 5
ymm5 = _mm256_load_ps((float *) (pIn + (5*MAT_SIZE))); // 行列 6
ymm6 = _mm256_load_ps((float *) (pIn + (6*MAT_SIZE))); // 行列 7
ymm7 = _mm256_load_ps((float *) (pIn + (7*MAT_SIZE))); // 行列 8
// 転置を開始
ymma = _mm256_unpacklo_ps(ymm0, ymm1); // 11,11,12,12,21,21,22,22
ymmb = _mm256_unpackhi_ps(ymm0, ymm1); // 13,13,14,14,23,23,24,24
ymmc = _mm256_unpacklo_ps(ymm2, ymm3); // 11,11,12,12,21,21,22,22
ymmd = _mm256_unpackhi_ps(ymm2, ymm3); // 13,13,14,14,23,23,24,24
ymme = _mm256_unpacklo_ps(ymm4, ymm5); // 11,11,12,12,21,21,22,22
ymmf = _mm256_unpackhi_ps(ymm4, ymm5); // 13,13,14,14,23,23,24,24
ymmg = _mm256_unpacklo_ps(ymm6, ymm7); // 11,11,12,12,21,21,22,22
ymmh = _mm256_unpackhi_ps(ymm6, ymm7); // 13,13,14,14,23,23,24,24
// 出力行 0、1、4、5 の作成
// 12, 12, 11, 11, 22, 22, 21, 21
ymm7 = _mm256_shuffle_ps(ymma, ymmc, 0x4e);
// 11, 11, 11, 11, 21, 21, 21, 21 (行 0 と行 4 の下半分)
ymm5 = _mm256_blend_ps(ymm7, ymma, 0x33);
// 12, 12, 12, 12, 22, 22, 22, 22 (行 1 と行 5 の下半分)
ymm3 = _mm256_blend_ps(ymm7, ymmc, 0xcc);
// 12, 12, 11, 11, 22, 22, 21, 21
ymm6 = _mm256_shuffle_ps(ymme, ymmg, 0x4e);
// 11, 11, 11, 11, 21, 21, 21, 21 (行 0 と行 4 の上半分)
ymm4 = _mm256_blend_ps(ymm6, ymme, 0x33);
// 12, 12, 12, 12, 22, 22, 22, 22 (行 1 と行 5 の上半分)
ymm2 = _mm256_blend_ps(ymm6, ymmg, 0xcc);
// 行 0、1、4、5 の作成の最終ステップ
// 8 つの行列から a11 を収集: 11,11,11,11,11,11,11,11 (行 0)
ymm_a11 = _mm256_permute2f128_ps(ymm5, ymm4, 0x20);
// 8 つの行列から a12 を収集: 12,12,12,12,12,12,12,12 (行 1)
ymm_a12 = _mm256_permute2f128_ps(ymm3, ymm2, 0x20);
// 8 つの行列から a21 を収集: 21,21,21,21,21,21,21,21 (行 4)
ymm_a21 = _mm256_permute2f128_ps(ymm5, ymm4, 0x31);
// 8 つの行列から a22 を収集: 22,22,22,22,22,22,22,22 (行 5)
ymm_a22 = _mm256_permute2f128_ps(ymm3, ymm2, 0x31);
// 出力行 2、3、6、7 の作成
// 14, 14, 13, 13, 24, 24, 23, 23
ymm7 = _mm256_shuffle_ps(ymmb, ymmd, 0x4e);
// 13, 13, 13, 13, 23, 23, 23, 23 (行 2 と行 6 の下半分)
ymm5 = _mm256_blend_ps(ymm7, ymmb, 0x33);
// 14, 14, 14, 14, 24, 24, 24, 24 (行 3 と行 7 の下半分)
ymm3 = _mm256_blend_ps(ymm7, ymmd, 0xcc);
// 14, 14, 13, 13, 24, 24, 23, 23
ymm6 = _mm256_shuffle_ps(ymmf, ymmh, 0x4e);
// 13, 13, 13, 13, 23, 23, 23, 23 (行 2 と行 6 の上半分)
ymm4 = _mm256_blend_ps(ymm6, ymmf, 0x33);
// 14, 14, 14, 14, 24, 24, 24, 24 (行 3 と行 7 の上半分)
ymm2 = _mm256_blend_ps(ymm6, ymmh, 0xcc);
// 行 2、3、6、7 の作成の最終ステップ
// 8 つの行列から a13 を収集: 13,13,13,13,13,13,13,13 (行 2)
ymm_a13 = _mm256_permute2f128_ps(ymm5, ymm4, 0x20);
// 8 つの行列から a14 を収集: 14,14,14,14,14,14,14,14 (行 3)
ymm_a14 = _mm256_permute2f128_ps(ymm3, ymm2, 0x20);
// 8 つの行列から a23 を収集: 23,23,23,23,23,23,23,23 (行 6)
ymm_a23 = _mm256_permute2f128_ps(ymm5, ymm4, 0x31);
// 8 つの行列から a24 を収集: 24,24,24,24,24,24,24,24 (行 7)
ymm_a24 = _mm256_permute2f128_ps(ymm3, ymm2, 0x31);
// 8 つの 4x4 行列の行 3 と行 4 の浮動小数点値を
// ymm レジスターに読み込む
ymm0 = _mm256_load_ps((float *)(pIn+(0*MAT_SIZE)+(2*MAT_WIDTH)));
ymm1 = _mm256_load_ps((float *)(pIn+(1*MAT_SIZE)+(2*MAT_WIDTH)));
ymm2 = _mm256_load_ps((float *)(pIn+(2*MAT_SIZE)+(2*MAT_WIDTH)));
ymm3 = _mm256_load_ps((float *)(pIn+(3*MAT_SIZE)+(2*MAT_WIDTH)));
ymm4 = _mm256_load_ps((float *)(pIn+(4*MAT_SIZE)+(2*MAT_WIDTH)));
ymm5 = _mm256_load_ps((float *)(pIn+(5*MAT_SIZE)+(2*MAT_WIDTH)));
ymm6 = _mm256_load_ps((float *)(pIn+(6*MAT_SIZE)+(2*MAT_WIDTH)));
ymm7 = _mm256_load_ps((float *)(pIn+(7*MAT_SIZE)+(2*MAT_WIDTH)));
// 転置を開始
ymma = _mm256_unpacklo_ps(ymm0, ymm1); // 31,31,32,32,41,41,42,42
ymmb = _mm256_unpackhi_ps(ymm0, ymm1); // 33,33,34,34,43,43,44,44
ymmc = _mm256_unpacklo_ps(ymm2, ymm3); // 31,31,32,32,41,41,42,42
ymmd = _mm256_unpackhi_ps(ymm2, ymm3); // 33,33,34,34,43,43,44,44
ymme = _mm256_unpacklo_ps(ymm4, ymm5); // 31,31,32,32,41,41,42,42
ymmf = _mm256_unpackhi_ps(ymm4, ymm5); // 33,33,34,34,43,43,44,44
ymmg = _mm256_unpacklo_ps(ymm6, ymm7); // 31,31,32,32,41,41,42,42
ymmh = _mm256_unpackhi_ps(ymm6, ymm7); // 33,33,34,34,43,43,44,44
// 出力行 0、1、4、5 の作成
// 32, 32, 31, 31, 42, 42, 41, 41
ymm7 = _mm256_shuffle_ps(ymma, ymmc, 0x4e);
// 31, 31, 31, 31, 41, 41, 41, 41 (行 0 と行 4 の下半分)
ymm5 = _mm256_blend_ps(ymm7, ymma, 0x33);
// 32, 32, 32, 32, 42, 42, 42, 42 (行 1 と行 5 の下半分)
ymm3 = _mm256_blend_ps(ymm7, ymmc, 0xcc);
// 32, 32, 31, 31, 42, 42, 41, 41
ymm6 = _mm256_shuffle_ps(ymme, ymmg, 0x4e);
// 31, 31, 31, 31, 41, 41, 41, 41 (行 0 と行 4 の上半分)
ymm4 = _mm256_blend_ps(ymm6, ymme, 0x33);
// 32, 32, 32, 32, 42, 42, 42, 42 (行 1 と行 5 の上半分)
ymm2 = _mm256_blend_ps(ymm6, ymmg, 0xcc);
// 行 0、1、4、5 の作成の最終ステップ
// 8 つの行列から a31 を収集: 31,31,31,31,31,31,31,31 (行 0)
ymm_a31 = _mm256_permute2f128_ps(ymm5, ymm4, 0x20);
// 8 つの行列から a32 を収集: 32,32,32,32,32,32,32,32 (行 1)
ymm_a32 = _mm256_permute2f128_ps(ymm3, ymm2, 0x20);
// 8 つの行列から a41 を収集: 41,41,41,41,41,41,41,41 (行 4)
ymm_a41 = _mm256_permute2f128_ps(ymm5, ymm4, 0x31);
// 8 つの行列から a42 を収集: 42,42,42,42,42,42,42,42 (行 5)
ymm_a42 = _mm256_permute2f128_ps(ymm3, ymm2, 0x31);
// 出力行 2、3、6、7 の作成
// 34, 34, 33, 33, 44, 44, 43, 43
ymm7 = _mm256_shuffle_ps(ymmb, ymmd, 0x4e);
// 33, 33, 33, 33, 43, 43, 43, 43 (行 2 と行 6 の下半分)
ymm5 = _mm256_blend_ps(ymm7, ymmb, 0x33);
// 34, 34, 34, 34, 44, 44, 44, 44 (行 3 と行 7 の下半分)
ymm3 = _mm256_blend_ps(ymm7, ymmd, 0xcc);
// 34, 34, 33, 33, 44, 44, 43, 43
ymm6 = _mm256_shuffle_ps(ymmf, ymmh, 0x4e);
// 33, 33, 33, 33, 43, 43, 43, 43 (行 2 と行 6 の上半分)
ymm4 = _mm256_blend_ps(ymm6, ymmf, 0x33);
// 34, 34, 34, 34, 44, 44, 44, 44 (行 3 と行 7 の上半分)
ymm2 = _mm256_blend_ps(ymm6, ymmh, 0xcc);
// 行 2、3、6、7 の作成の最終ステップ
// 8 つの行列から a33 を収集: 33,33,33,33,33,33,33,33 (行 2)
ymm_a33 = _mm256_permute2f128_ps(ymm5, ymm4, 0x20);
// 8 つの行列から a34 を収集: 34,34,34,34,34,34,34,34 (行 3)
ymm_a34 = _mm256_permute2f128_ps(ymm3, ymm2, 0x20);
// 8 つの行列から a43 を収集: 43,43,43,43,43,43,43,43 (行 6)
ymm_a43 = _mm256_permute2f128_ps(ymm5, ymm4, 0x31);
// 8 つの行列から a44 を収集: 44,44,44,44,44,44,44,44 (行 7)
ymm_a44 = _mm256_permute2f128_ps(ymm3, ymm2, 0x31);
// ******a11 の行列式*****************
__m256 ymm_a11a22, ymm_a33a44, ymm_a43a34, ymm_a11a23;
__m256 ymm_a32a44, ymm_a34a42, ymm_a11a24, ymm_a32a43;
__m256 ymm_a42a33;
__m256 ymm_a11a22_D, ymm_a11a23_D, ymm_a11a24_D, ymm_a11_D;
__m256 ymm_a33a44_a43a34, ymm_a32a44_a34a42, ymm_a32a43_a42a33;
// 8 つの行列の a11a22(a33a44 - a43a34) を計算
ymm_a11a22 = _mm256_mul_ps(ymm_a11, ymm_a22);
ymm_a33a44 = _mm256_mul_ps(ymm_a33, ymm_a44);
ymm_a43a34 = _mm256_mul_ps(ymm_a43, ymm_a34);
ymm_a33a44_a43a34 = _mm256_sub_ps(ymm_a33a44, ymm_a43a34);
ymm_a11a22_D = _mm256_mul_ps(ymm_a11a22, ymm_a33a44_a43a34);
// 8 つの行列の a11a23(a32a44 - a34a42) を計算
ymm_a11a23 = _mm256_mul_ps(ymm_a11, ymm_a23);
ymm_a32a44 = _mm256_mul_ps(ymm_a32, ymm_a44);
ymm_a34a42 = _mm256_mul_ps(ymm_a34, ymm_a42);
ymm_a32a44_a34a42 = _mm256_sub_ps(ymm_a32a44, ymm_a34a42);
ymm_a11a23_D = _mm256_mul_ps(ymm_a11a23, ymm_a32a44_a34a42);
// 8 つの行列の a11a24(a32a43 - a42a33) を計算
ymm_a11a24 = _mm256_mul_ps(ymm_a11, ymm_a24);
ymm_a32a43 = _mm256_mul_ps(ymm_a32, ymm_a43);
ymm_a42a33 = _mm256_mul_ps(ymm_a42, ymm_a33);
ymm_a32a43_a42a33 = _mm256_sub_ps(ymm_a32a43, ymm_a42a33);
ymm_a11a24_D = _mm256_mul_ps(ymm_a11a24, ymm_a32a43_a42a33);
// 8 つの行列の部分行列式を計算:
// (a11a22(a33a44 - a43a34) + a11a23(a32a44 - a34a42) +
// a11a24(a32a43 - a42a33))
ymm_a11a22_D = _mm256_sub_ps(ymm_a11a22_D, ymm_a11a23_D);
ymm_a11_D = _mm256_add_ps(ymm_a11a22_, ymm_a11a24_D);
// ******a12 の行列式*****************//
__m256 ymm_a12a21, ymm_a12a23, ymm_a31a44, ymm_a41a34,
__m256 ymm_a12a24, ymm_a31a43, ymm_a41a33;
__m256 ymm_a12a21_D, ymm_a12a23_D, ymm_a12a24_D, ymm_a12_D;
__m256 ymm_a31a44_a41a34, ymm_a31a43_a41a33;
// 8 つの行列の a12a21(a33a44 - a43a34) を計算
ymm_a12a21 = _mm256_mul_ps(ymm_a12, ymm_a21);
ymm_a12a21_D = _mm256_mul_ps(ymm_a12a21, ymm_a33a44_a43a34);
// 8 つの行列の a12a23(a31a44 - a41a34) を計算
ymm_a12a23 = _mm256_mul_ps(ymm_a12, ymm_a23);
ymm_a31a44 = _mm256_mul_ps(ymm_a31, ymm_a44);
ymm_a41a34 = _mm256_mul_ps(ymm_a41, ymm_a34);
ymm_a31a44_a41a34 = _mm256_sub_ps(ymm_a31a44, ymm_a41a34);
ymm_a12a23_D = _mm256_mul_ps(ymm_a12a23, ymm_a31a44_a41a34);
// 8 つの行列の a12a24(a31a43 - a41a33) を計算
ymm_a12a24 = _mm256_mul_ps(ymm_a12, ymm_a24);
ymm_a31a43 = _mm256_mul_ps(ymm_a31, ymm_a43);
ymm_a41a33 = _mm256_mul_ps(ymm_a41, ymm_a33);
ymm_a31a43_a41a33 = _mm256_sub_ps(ymm_a31a43, ymm_a41a33);
ymm_a12a24_D = _mm256_mul_ps(ymm_a12a24, ymm_a31a43_a41a33);
// 8 つの行列の部分行列式を計算:
// (a12a21(a33a44 - a43a34) + a12a23(a31a44 - a41a34)
// + a12a24(a31a43 - a41a33))
ymm_a12a21_D = _mm256_sub_ps(ymm_a12a23_D, ymm_a12a21_D);
ymm_a12_D = _mm256_sub_ps(ymm_a12a21_D, ymm_a12a24_D);
// ******a13 の行列式*****************//
__m256 ymm_a13a21, ymm_a13a22, ymm_a13a24, ymm_a31a42;
__m256 ymm_a41a32;
__m256 ymm_a13a21_D, ymm_a13a22_D, ymm_a13a24_D, ymm_a13_D;
__m256 ymm_a31a42_a41a32;
// 8 つの行列の a13a21(a32a44 - a42a34) を計算
ymm_a13a21 = _mm256_mul_ps(ymm_a13, ymm_a21);
ymm_a13a21_D = _mm256_mul_ps(ymm_a13a21, ymm_a32a44_a34a42);
// 8 つの行列の a13a22(a31a43 - a41a33) を計算
ymm_a13a22 = _mm256_mul_ps(ymm_a13, ymm_a22);
ymm_a13a22_D = _mm256_mul_ps(ymm_a13a22, ymm_a31a43_a41a33);
// 8 つの行列の a13a24(a31a42 - a41a32) を計算
ymm_a13a24 = _mm256_mul_ps(ymm_a13, ymm_a24);
ymm_a31a42 = _mm256_mul_ps(ymm_a31, ymm_a42);
ymm_a41a32 = _mm256_mul_ps(ymm_a41, ymm_a32);
ymm_a31a42_a41a32 = _mm256_sub_ps(ymm_a31a42, ymm_a41a32);
ymm_a13a24_D = _mm256_mul_ps(ymm_a13a24, ymm_a31a42_a41a32);
// 8 つの行列の部分行列式を計算:
// (a13a21(a32a44 - a42a34) + a13a22(a31a43 - a41a33)
// + a13a24(a31a42 - a41a32))
ymm_a13a21_D = _mm256_sub_ps(ymm_a13a21_D, ymm_a13a22_D);
ymm_a13_D = _mm256_add_ps(ymm_a13a21_D, ymm_a13a24_D);
// ******a14 の行列式*****************//
__m256 ymm_a14a21, ymm_a14a22, ymm_a14a23;
__m256 ymm_a14a21_D, ymm_a14a22_D, ymm_a14a23_D, ymm_a14_D;
// 8 つの行列の a14a21(a32a43 - a42a33) を計算
ymm_a14a21 = _mm256_mul_ps(ymm_a14, ymm_a21);
ymm_a14a21_D = _mm256_mul_ps(ymm_a14a21, ymm_a32a43_a42a33);
// 8 つの行列の a14a22(a31a43 - a41a33) を計算
ymm_a14a22 = _mm256_mul_ps(ymm_a14, ymm_a22);
ymm_a14a22_D = _mm256_mul_ps(ymm_a14a22, ymm_a31a43_a41a33);
// 8 つの行列の a14a23(a31a42 - a41a32) を計算
ymm_a14a23 = _mm256_mul_ps(ymm_a14, ymm_a23);
ymm_a14a23_D = _mm256_mul_ps(ymm_a14a23, ymm_a31a42_a41a32);
// 8 つの行列の部分行列式を計算:
// (a14a21(a32a43 - a42a33)) + a14a22(a31a43 - a41a33)
// + a14a23(a31a42 - a41a32))
ymm_a14a21_D = _mm256_sub_ps(ymm_a14a22_D, ymm_a14a21_D);
ymm_a14_D = _mm256_sub_ps(ymm_a14a21_D, ymm_a14a23_D);
// 8 つの行列の最終行列式を計算:
// a11、a12、a13、a14 の行列式を加算
ymm_a11_D = _mm256_add_ps(ymm_a11_D, ymm_a12_D);
ymm_a13_D = _mm256_add_ps(ymm_a13_D, ymm_a14_D);
ymm_a11_D = _mm256_add_ps(ymm_a11_D, ymm_a13_D);
// 行列 D の個々の値をデスティネーションに分散/抽出
_mm256_store_ps((float *)pOut, ymm_a11_D);
}
著者紹介
Pallavi Mehrotra - Motorola 社で CDMA Network Infrasturcture のソフトウェア開発を経て、2006 年にシニア・ソフトウェア・エンジニアとしてインテルに入社。現在、SSG Apple 推進チームのメンバーとして、パワーとパフォーマンスを向上するべく Mac OS* X アプリケーションの最適化に取り組んでいます。アリゾナ州立大学でコンピューター・サイエンスの修士号を、インドで電気工学の学士号を取得しています。
Richard Hubbard – シニア・ソフトウェア・エンジニア。SSG Apple 推進チームのメンバーとして、パワーとパフォーマンスを向上するべく Mac OS* X アプリケーションの最適化に取り組んでいます。スティーブンス工科大学で電気工学の修士号を、ニュージャージー工科大学でコンピューター工学の学士号を取得しています。
インテル® ソフトウェア製品のパフォーマンス/最適化に関する詳細は、最適化に関する注意事項 (英語) を参照してください。
編集部追加
最新のインテル® MKL やインテル® IPP の各ルーチンは、本記事で取り上げられたような技術によってインテル® AVX 搭載プロセッサー向けにも最適化済みです。これらのライブラリー製品もバンドルされているインテル® C++/Fortran Composer XE を是非ともお試しください。評価版のダウンロード、お問い合わせはエクセルソフト株式会社まで。
なお、本記事にてダウンロードできるサンプルコードの中には既知の問題があります。ヘッダーファイルについて gmmintrin.h ではなく immintrin.h をインクルードするようにしてください。
参考(英語):http://software.intel.com/en-us/articles/catastrophic-error-could-not-open-source-file-gmmintrinh/


