この記事は、Codeplay Blogs に公開されている「Simulating Crowd Simulation with SYCL」の日本語参考訳です。原文は更新される可能性があります、原文と翻訳文の内容が異なる場合原文を優先してください。
この記事の PDF 版はこちらからご利用になれます。
Dirk Helbing は、1995年にランジュバン方程式を用いて群衆の挙動をモデル化することを目的とした「Social Force Model for Pedestrian Dynamics」を発表し[1]、2000年の論文「Simulating Dynamical Features of Escape Panic」[2] では、より洗練されたモデルを提案しています。世界初の商用 GPU は、Helbing の最初の論文発表から 4年後に市場に登場し、コンピューティングの状況を一変させました。Helbing が概説したような負荷の重い作業を、GPU にオフロードして並列処理できるようになったのです。この記事では、Social Force Model を例に、SYCL* を使用して、効率良くパフォーマンスの移植性に優れた計算集約型モデルの実装を開発する方法を示します。
モデル
Helbing は、大群衆の中での歩行者の行動は、目的地へ進もうとする力、周囲の人から受ける反発力、障害物から受ける反発力という 3 つの要素によって決定されるとしています。これらの力は、以下の微分方程式の基礎を形成し、これを積分することで歩行者の速度を算出できます。
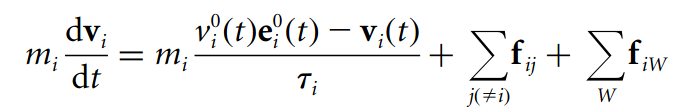
この数式を分かりやすく表現すると、以下のようになります。
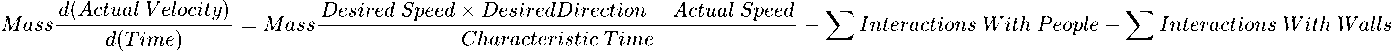
Helbing のモデルは N 体シミュレーションなどの粒子システムに似ていますが、物理的な力は精神的・社会的な衝動に置き換わっており、歩行者は他者や障害物に近づきすぎないようにしながら、目的地に向かって進みます。
Helbing のモデルを直感的に理解することで、このようなシステムの並列化をどのように進めるべきかを検討できます。2D グラフィックスは SDL で描画します。シミュレーションと並行して、モデルの統計情報を確認すると役立ちます。
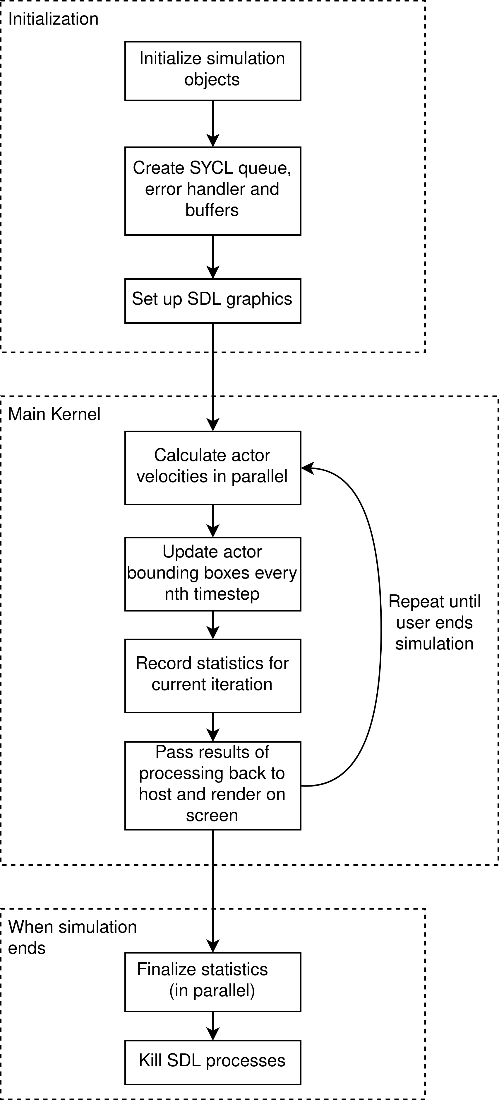
このプロジェクトには、主に 3 つの並列化インスタンスがあり、それぞれ個別のカーネルにマッピングされます。
- 必要な計算回数を考慮すると、最も計算量の多いカーネルは歩行者の速度の計算であると推測されます。各歩行者は個別の SYCL* ワークアイテムになります。
- 歩行者の境界ボックスは並列に更新されます。
- 統計の記録と集計には、タイムステップごとに歩行者の状態をチェックするカーネルと、平均値を計算するリダクション・カーネルを使用します。
GPU での群衆シミュレーションは、計算依存ではなく、実行される計算もそれほどコストが高くなく、SIMD アーキテクチャーに適しています。しかし、メモリー転送がパフォーマンス・ボトルネックになります。そのため、コストの高いデータ転送の完了を待つ間、GPU がアイドル状態になる時間をできるだけ短くすることが、設計上の重要なポイントになります。
主なカーネル
このモデルの主な処理は、differentialEq 関数で歩行者の力を計算することです。differentialEq は、シミュレーションが実行されている間、タイムステップごとに各歩行者に対して並列に呼び出されます。つまり、differentialEq の各呼び出しは、GPU の 1 つのコアにマップされる 1 つのワークアイテムになります。GPU は、別々のコアで別々のスレッドを同時に実行することができます。これは、コンピューティングにおける並列処理の基本です。この実装では、幾何ベクトル (歩行者の位置、速度などを表す) は、sycl::float2 変数として実装されています。これは、SYCL* がこれらの型に対してベクトルと SIMD 数値演算を定義しているためです。differentialEq カーネルは次のように呼び出されます。
myQueue.submit([&](sycl::handler &cgh) {
// デバイス上のデータにアクセスするアクセサーを作成
auto actorAcc =
actorBuf.get_access<sycl::access::mode::read_write>(cgh);
auto wallsAcc = wallsBuf.get_access<sycl::access::mode::read>(cgh);
auto pathsAcc = pathsBuf.get_access<sycl::access::mode::read>(cgh);
auto heatmapEnabledAcc =
heatmapEnabledBuf.get_access<sycl::access::mode::read>(cgh);
cgh.parallel_for(
sycl::range<1>{actorAcc.size()}, [=](sycl::id<1> index) {
if (!actorAcc[index].getAtDestination()) {
differentialEq(index, actorAcc, wallsAcc,
pathsAcc, heatmapEnabledAcc);
}
});
});
ここで気を付けなければならないことは、通常、SYCL* カーネルは異なる翻訳単位から関数を呼び出せないということです。呼び出すとコンパイル時にエラーが発生し、問題の関数がカーネルの翻訳ユニットの範囲内で定義されていないことが通知されます。DPC++ では、関数宣言に SYCL_EXTERNAL マクロを追加することでこれを解決できます。SYCL_EXTERNAL は、デバイス上で呼び出されるすべての関数に対して外部リンクを可能にします。SYCL_EXTERNAL は、SYCL* 仕様ではオプションとして定義されているため、すべての SYCL* 実装でサポートが保証されているわけではありません。サポートされていない場合、カーネル内から呼び出される関数は、カーネルと同じヘッダーファイル内で宣言し、両者を同じ翻訳ユニットに配置します。differentialEq は、まず各歩行者の目的地へ進もうとする力を計算します。
// 歩行者の目的地へ進もうとする力を計算
float mi = currentActor->getMass(); // 歩行者の質量
float v0i = currentActor->getDesiredSpeed(); // 想定速度
sycl::float4 destination =
paths[currentActor->getPathId()]
.getCheckpoints()[currentActor->getDestinationIndex()];
// デスティネーション領域内の歩行者に最も近い点の方向ベクトルを計算
std::pair<float, sycl::float2> minRegionDistance;
std::array<sycl::float2, 4> destinationRect = {
sycl::float2{destination[0], destination[1]},
sycl::float2{destination[2], destination[1]},
sycl::float2{destination[2], destination[3]},
sycl::float2{destination[0], destination[3]}};
for (int x = 0; x < 4; x++) {
int endIndex = x == 3 ? 0 : x + 1;
auto dniw =
getDistanceAndNiw(currentActor->getPos(),
{destinationRect[x], destinationRect[endIndex]});
if (dniw.first < minRegionDistance.first || minRegionDistance.first == 0) {
minRegionDistance = dniw;
}
}
minRegionDistance.second = normalize(minRegionDistance.second);
sycl::float2 e0i = {-minRegionDistance.second[0], // 想定方向
-minRegionDistance.second[1]};
sycl::float2 vi = currentActor->getVelocity(); // 実際の速度
sycl::float2 personalImpulse = mi * (((v0i * e0i) - vi) / Ti);
// Ti は「特性時間」を示す定数
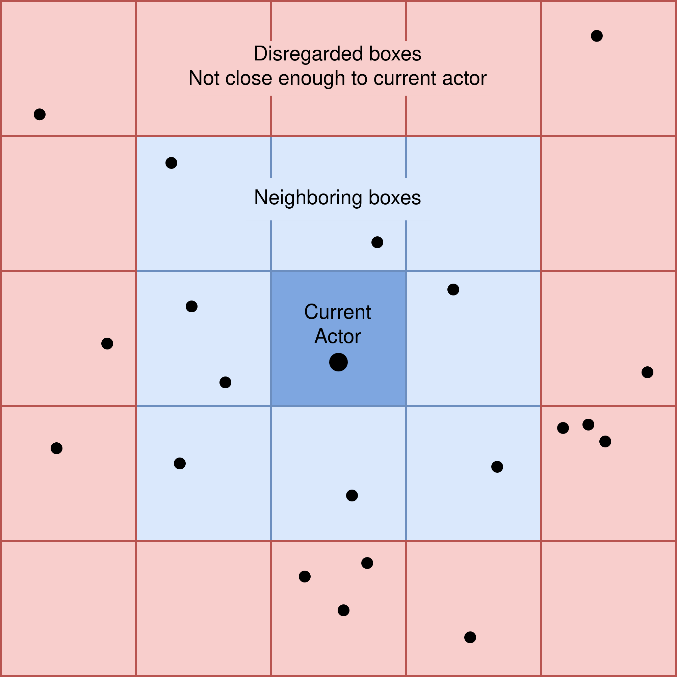
これは非常に単純な計算であり、最もコストのかかる処理は、デスティネーション領域で歩行者に最も近い点の方向ベクトルの計算です (デスティネーションが点ではなく矩形領域として定義されているため、この計算が必要になります)。歩行者の目的地へ進もうとする力を計算したら、次に周囲の人から受ける反発力を計算します。初期の最適化として必要だと考えたのが、境界ボックスの実装です。シミュレーションが行われる空間はグリッドに分割され、各歩行者は所属するボックスの属性を待ちます。周囲の反発力の計算では、現在の歩行者から離れた場所にいる歩行者は影響力がないと見なし、現在の歩行者の境界ボックスと隣接する 8 つのボックス内の歩行者のみを考慮します。各歩行者の境界ボックスは、20 タイムステップごとに並列に更新されます。
// 歩行者の境界ボックスを更新
myQueue.submit([&](sycl::handler &cgh) {
auto actorAcc = actorBuf.get_access<sycl::access::mode::read_write>(cgh);
cgh.parallel_for(sycl::range<1>{actorAcc.size()}, [=](sycl::id<1> index) {
Actor *currentActor = &actorAcc[index];
sycl::float2 pos = currentActor->getPos();
int row = sycl::floor(pos[0]);
int col = sycl::floor(pos[1]);
currentActor->setBBox({row, col});
});
});
myQueue.throw_asynchronous();
これは最適な境界ボックスの実装ではなく、再検討の余地があります。データを Actor クラスの属性として保存すると、メモリーアクセスの結合によるパフォーマンスの利点が得られません。最適な実装は、各境界ボックスの歩行者のリストを維持することです。このアプローチの問題点は、各境界ボックスのリストは動的なサイズであるべきですが、SYCL* はカーネルで静的なコンテナしか使用できません。この問題は、ポインターのリンクリストによって回避できる可能性がありますが、シリアルアクセスが強制されるため、GPU パフォーマンスが低下します。とは言うものの、現在の最適でない実装でも、ベンチマークを実行したところ、実行時間が 29% 短縮されました。
境界ボックスを使用して計算回数を減らし、以下の方法で各歩行者の周囲の反発力を計算します。
// (有効な境界ボックス内の) 周囲の人から受ける反発力を計算
sycl::float2 peopleForces = {0, 0};
for (int x = 0; x < actors.size(); x++) {
Actor neighbour = actors[x];
bool bBoxFlag = std::any_of(neighbourBoxes.begin(), neighbourBoxes.end(),
[neighbour](std::array<int, 2> i) {
return i[0] == neighbour.getBBox()[0] &&
i[1] == neighbour.getBBox()[1];
});
if (actorIndex != x && !neighbour.getAtDestination() && bBoxFlag) {
// 歩行者から周囲の歩行者への方向ベクトル
sycl::float2 currentToNeighbour = pos - neighbour.getPos();
// 歩行者と周囲の歩行者の距離
float dij = magnitude(currentToNeighbour);
// 結合半径
float rij = neighbour.getRadius() + currentActor->getRadius();
// 正規化された方向ベクトル
sycl::float2 nij = currentToNeighbour / dij;
// 接線方向ベクトル
sycl::float2 tij = getTangentialVector(nij);
float g = dij > rij ? 0 : rij - dij;
float deltavtij = dotProduct(
(neighbour.getVelocity() - currentActor->getVelocity()), tij);
peopleForces += (PEOPLEAi * sycl::exp((rij - dij) / Bi) + K1 * g) * nij +
(K2 * g * deltavtij * tij);
}
}
次に、障害物から受ける反発力を計算します。これには、経路上の歩行者に最も近いポイントを見つけるため、いくつかの複雑なベクトル計算が必要です。ここで使用するヘルパー関数は、MathHelper.cpp で定義されています。
// 障害物から受ける反発力を計算
sycl::float2 wallForces = {0, 0};
for (int x = 0; x < walls.size(); x++) {
std::array<sycl::float2, 2> currentWall = walls[x];
float ri = currentActor->getRadius();
// 障害物までの距離と正規化された方向ベクトル
std::pair<float, sycl::float2> dAndn = getDistanceAndNiw(pos, currentWall);
float diw = dAndn.first;
float g = diw > ri ? 0 : ri - diw;
sycl::float2 niw = normalize(dAndn.second);
// 接線方向ベクトル
sycl::float2 tiw = getTangentialVector(niw);
wallForces += (WALLAi * sycl::exp((ri - diw) / Bi) + K1 * g) * niw -
(K2 * g * dotProduct(vi, tiw) * tiw);
}
ここでは、Helbing のモデルに力のランダムな変動を導入して、現実の群衆で観察されるような予測不可能性をシミュレーションに取り入れます。この実装の詳細については、次のセクションで説明します。また、受けた反発力に応じて歩行者を色分けすることで、群衆のどこで力が最も強くなっているかを視覚化するヒートマップを生成できます。これは緊急避難シナリオのモデル化において重要な機能ですが、デバッグにも役立ちます。反発力を計算し、変動を適用したら、最後のステップでは、一定のタイムステップでシミュレーションを実行し、歩行者が目的地に到達したかどうかをチェックします。
// 積分を計算
sycl::float2 acceleration = forceSum / mi;
currentActor->setVelocity(vi + acceleration * TIMESTEP);
currentActor->setPos(pos + currentActor->getVelocity() * TIMESTEP);
currentActor->checkAtDestination(
destination, paths[currentActor->getPathId()].getPathSize());
GPU での乱数生成
標準ライブラリーの乱数ジェネレーターは GPU から呼び出すことができません。インテル® oneMKL は SYCL* 向けに効率良い RNG を提供していますが、新しいことを学ぶという精神から、George Marsaglia の論文[3] に基づいて XOR シフト RNG を実装することにしました。XOR シフト・ジェネレーターは、このユースケースで目的の効果を達成するのに十分なランダム性を持ち、大きなオーバーヘッドを引き起こさない程度に高速です。各歩行者の RNG は、初期化中に std::uniform_int_distribution を使用してホスト側でシードが設定されます。
以下は、XOR シフト疑似乱数ジェネレーターの実装です。
// George Marsaglia が開発した XOR シフト RNG
// https://www.jstatsoft.org/article/download/v008i14/916
SYCL_EXTERNAL uint randXorShift(uint state) {
state ^= (state << 13);
state ^= (state >> 17);
state ^= (state << 5);
return state;
}
統計の照合
統計の照合は 2 つの関数に分かれています。
updateStatsはタイムステップごとに呼び出され、歩行者に加えられる平均的な力、反復の実行時間、タイムステップ中に歩行者が目的地に到達した場合はかかった時間などを記録します。finalizeStatsは実行終了時に呼び出され、結果をテキストファイルに書き込む前に平均カーネル時間を計算します。
結果を使用し、GenerateGraphs.py を実行してグラフを生成できます。どちらの関数も、SYCL* 2020 で導入されたリダクション・カーネル機能を使用しており、開発者は独自の並列リダクションを実装する手間を省くことができます。
// リダクション・カーネルを使用して平均カーネル時間を計算
myQueue.submit([&](sycl::handler& cgh) {
auto durationAcc =
kernelDurationsBuf.get_access<sycl::access::mode::read>(cgh);
auto sumReduction = sycl::reduction(durationSumBuf, cgh, sycl::plus<int>());
auto out = sycl::stream{64, 1028, cgh};
cgh.parallel_for(
sycl::range<1>{durationAcc.size()}, sumReduction,
[=](sycl::id<1> index, auto& sum) { sum += durationAcc[index]; });
});
最適化と学んだこと
このプロジェクトの開発は、繰り返しのプロセスでした。最初のバージョンは、現在の状態に至るまで多くの改良とパフォーマンスの最適化が行われました。このプロセスでは、インテル® VTune™ プロファイラーや NVIDIA Nsight* Systems などのプロファイル・ツールを使用し、GPU プログラミングの理論的な違いについての理解を深めました。
主なカーネルでよく行われる処理に、ベクトルの正規化があります。平方根の計算はコストがかかるため、ベクトルの正規化に多用すると、多くのオーバーヘッドが発生します。対応策として、同僚が「高速逆平方根」という手法を教えてくれました。これは、ファーストパーソン・シューティング・ゲーム『Quake III』の開発者が発見した、数値計算法により逆平方根を素早く計算する方法です。SYCL* には、逆平方根を計算する独自の sycl::rsqrt メソッドがあります。この最適化を適用したところ、実行時間が 2.63% 短縮されました。
前述のとおり、ここで扱うシステムは計算依存ではなく、メモリー依存です。NVIDIA Nsight* Systems を使用して CUDA* バックエンドのパフォーマンスをプロファイルしたところ、基準を満たしていないメモリー・アクセス・パターンが明らかになりました。以下は、1 反復の最初の nsys 出力です (境界ボックスの更新を含む)。
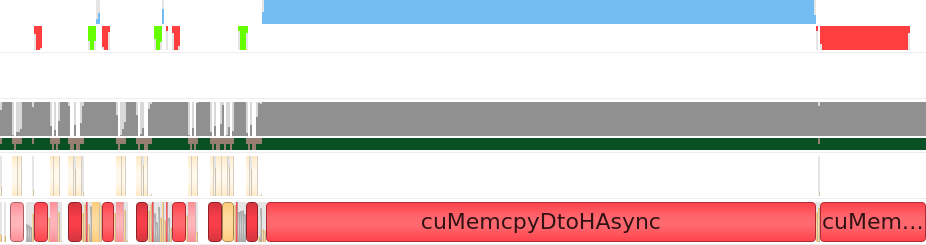
nsys 出力は、非常に多くのメモリー転送が行われていることを示しています。一番上の行の小さな青いカーネルは、その下の行にある対称的なメモリー転送操作 (緑と赤のブロック) に囲まれています。2 つの小さなカーネルは、統計情報の更新と歩行者の境界ボックスの変更を行い、大きなカーネルは力の計算を行います。現在のメモリー・アクセス・パターンは、カーネルごとに新しいバッファーを作成し、カーネルが完了すると削除します。バッファーの作成と削除はコストの高い操作であり、特に削除ブロックはデータがデバイスからホストに転送されるまで待機しなければならず、不要なオーバーヘッドが多く発生します。データは反復ごとに 1 回だけデバイスにコピーし、各カーネル間でデバイスに留まり、処理結果を画面に表示する必要があるときだけホストに戻すべきです。修正後のアプローチは、初期化中にバッファーを一度作成し、各反復の開始時にその内容をデバイスに一度コピーし、必要なときにデバイス上のデータにアクセスするには sycl::host_accessor を使用します。これにより、次のような nsys 出力になりました。
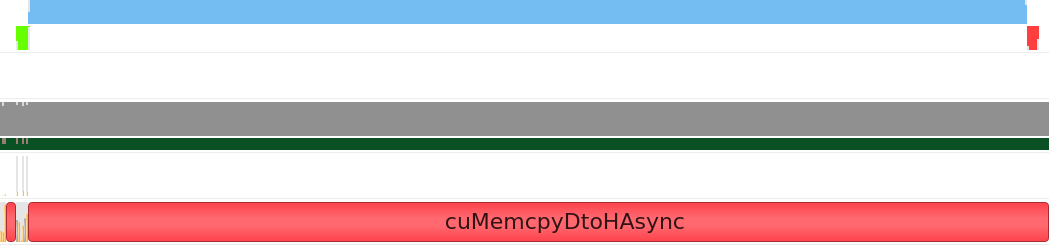
この出力の最初の 2 つの行では、1 つの緑のブロックはホストからデバイスへのコピー操作を示し、次に 3 つのカーネルがメモリー転送を待つことなく連続して実行され、最後に host_accessor が作成されるとデータがホストにコピーバックされていることが分かります。同じバッファーが再利用されているため、host_accessor の作成によって明示的にアクセスを要求しない限り、すべてのデータはカーネル間でデバイス上に残ります。
キューへの投入が完了するたび、当初は queue.wait_and_throw を呼び出していました。これにより、プログラムがすべてのキュー操作の完了を待機し、ランタイムエラーをスローする間、ブロッキング操作が発生します。しかし、SYCL* のバッファー/アクセサーモデルを使用する場合、すべてのコマンドの後に待機することはお勧めしません。代わりに、SYCL* ランタイムがカーネル間で依存関係を持つことを許可すべきです。SYCL* は、バッファーの暗黙のデータ移動をサポートしています。つまり、SYCL* ランタイムはコマンドグループのアクセス要件から依存関係やデータ移動を推測します。例えば、バッファー A がカーネル 1 で変更され、その後カーネル 2 で使用される場合、SYCL* ランタイムは、カーネル 1 がバッファー A を終了するまで待ってからカーネル 2 に移ることを知っているので、キューで明示的 に wait を呼び出す必要はありません。したがって、これらの wait_and_throw の呼び出しは、throw_asynchronous に置き換えることができます。
このプロジェクトの最も基本的な設計ミスの 1 つで、最大のパフォーマンス・ボトルネックの原因となったのは、主な Actor クラスに配列構造体 (SoA) ではなく、構造体配列 (AoS) レイアウトを採用したことでした。GPU はグローバルメモリーにアクセスする際に、単一のメモリーアドレスではなく、メモリーブロックにアクセスします。したがって、メモリー内のデータの配置方法がパフォーマンスに影響を与える可能性があります。従来の構造体配列でオブジェクトを格納すると、メモリー内で属性は以下のように配置されます。
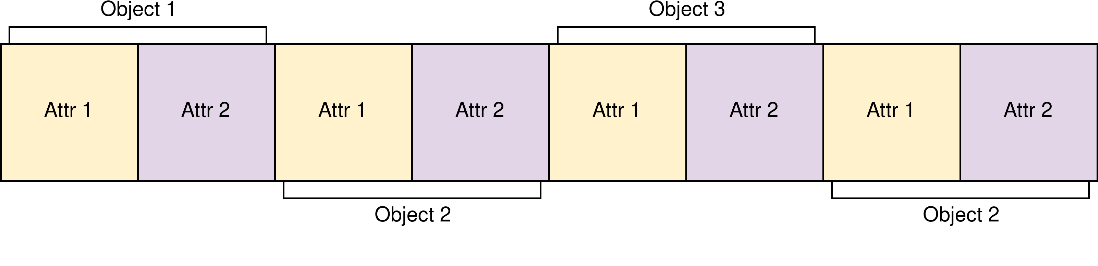
配列構造体を使用すると、以下のようになります。
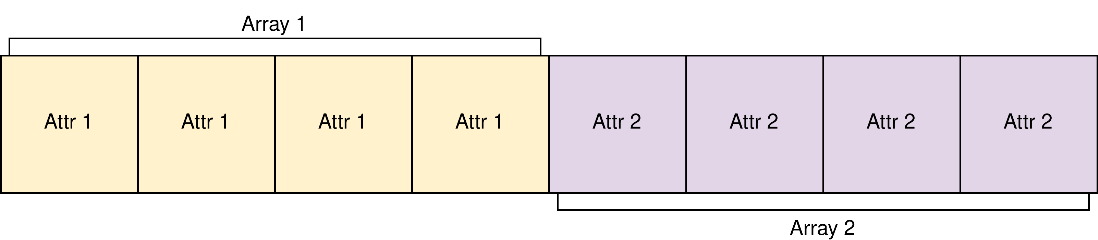
GPU は 4 ブロックのチャンクでメモリーにアクセスすると仮定します。AoS で Attr1 の値をすべて収集しようとすると、GPU は必要なデータをすべて取得するため 2 回のメモリーアクセス操作を必要とします。しかし、SoA を使えば、1 回のメモリーアクセスですべてを取得できます。一般に、メモリー上で物理的に近い位置にあるデータへのアクセスは、メモリーアクセスを結合できるため、効率良く行うことができます。現在、プロジェクトは AoS を使用しています。SoA に移行することで、特にメモリー依存のシステムであることから、大きなパフォーマンス向上が期待できますが、トレードオフとして、コードの全面的な再構築が必要になります。
結果

上記の画像は、5000 人の歩行者が 2 つのグループに分かれて互いに突進していく様子を示す動画からの抜粋です。これは、Helbing が群衆の研究で観察した重要な現象であり、モデルに模倣させたいと考えた「避難経路の形成」を示しています。目的地の異なる 2 つの群衆が出会うと、同じ目的地を持つ歩行者は、後ろの群衆の勢いに押されて進む「リーダー」によって切り開かれたいくつかの異なる経路を形成します。
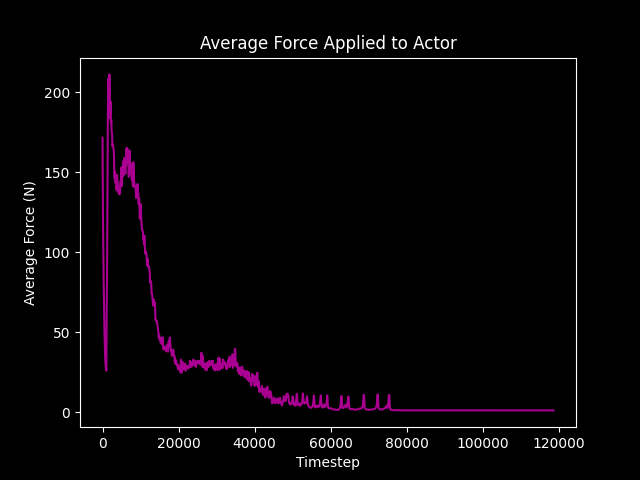
各反復中に各歩行者が受ける平均的な力をグラフにすると、2 つの群衆が衝突し、経路が形成されるときに、平均的な力が最も大きくなることが分かります。2 つの群衆がすれ違い、歩行者が衝突エリアから抜け出し始めると、平均的な力は徐々に小さくなります。1分45秒以降の映像では、歩行者が空いたスペースに広がることで、群衆の密度が下がり始めているのが確認できます。
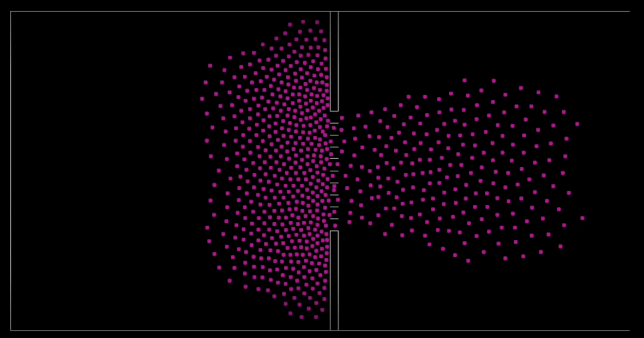
次のシミュレーションは、群衆シミュレーションのアルゴリズムを使用して、緊急避難シナリオにおける建物のレイアウトをテストする方法を示しています。この環境は、スタジアムや会場の入り口をモデル化したもので、多くの場合、障壁を設置して、人々が吸い込まれるように通り抜ける経路を形成しています。群衆が移動する空間を経路に分割すると、群衆のスループットを低下させる効果があり、歩行者は障害物を通過した後、目的地に到達するため、より多くの時間と空間を確保できます。経路がなくなると、群衆はより速く目的地に到着しますが、勢いを吸収する障害物もなく、無制限に人々が同じ場所に集まると、怪我などの危険性が高まります。

最後の出力例は、4 つのグループが交差点で衝突するというものです。このシナリオは、「faster is slower effect」と呼ばれるものの好例です。上記の画像では、紫の群衆が他の 3 つのグループよりも速度が速いことが観察できます。しかし、紫の群衆を他のグループと同じ速度にすると、紫の群衆は速い速度で移動しているときよりも早く目的地に到着することが分かりました。これは、すべてのグループが同じ速度で移動することで、グループ同士がより整然と通り過ぎるという自己組織化のようなものが生まれるからです。しかし、紫の群衆がより速い速度で移動すると、この自然な秩序が崩れ、行き詰まりや停滞が頻繁に起こるようになります。
移植性の高いコード
SYCL* は、開発者がパフォーマンスを犠牲にすることなく、移植性の高いコードを記述できるようにします。このプロジェクトは、OpenCL*、CUDA*、HIP バックエンドのデバイス向けにコンパイルできます。ここでは、OpenCL* を実行するインテル® Iris® Xe グラフィックス上と CUDA* を実行する NVIDIA* Titan RTX* GPU 上で実行しました。インテグレーテッド・グラフィックスとディスクリート・グラフィックスという 2 つの全く異なるデバイス上で、プロファイル・モードで実行しました。つまり、SDL レンダリングによるオーバーヘッドがありません (CMake フラグ –DPROFILING_MODE で有効にできます)。
シミュレーション・エンジンは、JSON ファイルを入力として受け取り、シミュレーションの環境とパラメーターを設定します。この入力ファイルのフォーマットは、プロジェクトの README で説明されています。入力ファイルの例は、Python* スクリプト InputFileGenerator.py によって生成されます。歩行者の数や反復回数を変えてこれらのテストを実行し、カーネル実行への影響を確認できます。
群集シミュレーションのコードは、https://github.com/codeplaysoftware/sycl-crowd-simulation (英語) リポジトリーにあります。
参考文献
- [1] Helbing, Dirk & Molnar, Peter. (1995). Social Force Model for Pedestrian Dynamics. Physical Review E. 51. 10.1103/PhysRevE.51.4282. https://arxiv.org/abs/cond-mat/9805244
- [2] Helbing, D., Farkas, I. & Vicsek, T. Simulating dynamical features of escape panic. Nature 407, 487–490 (2000). https://doi.org/10.1038/35035023
- [3] Marsaglia, G. (2003). Xorshift RNGs. Journal of Statistical Software, 8(14), 1–6. https://doi.org/10.18637/jss.v008.i14
法務上の注意書き
性能は、使用状況、構成、その他の要因によって異なります。
性能の測定結果はシステム構成の日付時点のテストに基づいています。また、現在公開中のすべてのセキュリティー・アップデートが適用されているとは限りません。構成の詳細は、補足資料を参照してください。絶対的なセキュリティーを提供できる製品またはコンポーネントはありません。
実際の費用と結果は異なる場合があります。
インテルのテクノロジーを使用するには、対応したハードウェア、ソフトウェア、またはサービスの有効化が必要となる場合があります。
Codeplay Software Ltd has published this article only as an opinion piece. Although every effort has been made to ensure the information contained in this post is accurate and reliable, Codeplay cannot and does not guarantee the accuracy, validity or completeness of this information. The information contained within this blog is provided "as is" without any representations or warranties, expressed or implied. Codeplay Sofware Ltd makes no representations or warranties in relation to the information in this post.


