この記事は、インテル® ソフトウェア・ネットワークに掲載されているブログ「Statistical Summary Library Overview」(http://software.intel.com/en-us/articles/statistical-summary-library-overview/) の日本語参考訳です。
統計的計算の精度とパフォーマンスが強化された最新のアルゴリズムを提供する、最適化された並列ライブラリーがインテル® MKL 10.3 で実装されました。インテル® MKL のサマリー統計ライブラリー (SSL) の詳細は、「インテル® MKL の SSL の概要」 (http://software.intel.com/file/27692) を参照してください。
- 膨大な量の情報を管理する方法
- 一度に複数の推定値を計算する
- データをより小さなチャンク (塊) に分割して処理するには?
- データセット内の外れ値を検出するには?
- マルチコアを活用しよう
- アップデートで追加された新機能
- 外れ値検出アルゴリズムはどの程度速いのか?
- ロバスト手法の使用方法
- 欠測値の処理方法
膨大な量の情報を管理する方法
インテル® MKL のサマリー統計ライブラリーは、多次元データセットの並列統計処理ソリューションです。ローデータの初期統計解析を行う関数が含まれており、データセットの構造を調査し、基本的な特徴、推定、および内部依存性を取得します。
サマリー統計ライブラリーには、データセットのさまざまな統計的推定値を計算する豊富なツール群が用意されています。
- 代数積率と中心積率 (最大 4 次まで)、歪度、尖度、変動係数、分位数、および順序統計量を計算する関数
- データセット内の依存性を予測するアルゴリズム: 分散共分散/相関行列、偏分散共分散/相関行列、プールされた/グループ化された分散共分散/相関行列。また、外れ値が存在する場合に、データの共分散行列および平均のロバスト推定を計算することもできます。
- データセット内の外れ値を検出するツール
- 欠測値を含むデータを効率良く処理するアルゴリズム
サマリー統計ライブラリーのアルゴリズムは、一度に解析するには大きすぎるために複数のチャンクに分けて処理されるデータをサポートします。(特に、分散共分散行列、代数積率と中心積率、歪度、尖度、および変動係数のような基礎統計推定量)
サマリー統計ライブラリーは、フルおよびパックド形式の分散共分散行列、行および列格納形式のデータセットをサポートしています。
サマリー統計ライブラリーは、単精度および倍精度の浮動小数点演算をサポートしています。
サマリー統計ライブラリーのアルゴリズムは、マルチコア・プロセッサーを活用できるように設計されています。
サマリー統計ライブラリーの API は、FORTRAN 90 および C/89 言語のインターフェイスを提供します。
一度に複数の推定値を計算する
今日、私はデータセットの統計的推定値を計算しなければなりませんでした。測定値は重み付けされており、乱数ベクトルの一部のコンポーネントだけを解析する必要がありました。日常生活の中で、このような作業をどの程度頻繁に行い、どのように行っていますか? ほとんど行っていない場合やサイズが小さな場合は、一般的な統計パッケージやデータ処理プログラムを使用すると良いでしょう。例えば、定期的に大規模なデータ配列を処理して、遺伝子の発現量を解析しなければならないとしたらどうしますか? どうしたら推定値を迅速に計算できるでしょうか。インテル® MKL のサマリー統計ライブラリーは、このような処理に適しています。
ライブラリーを使用する一般的なアプリケーションは 4 つのステップで構成されます。ここでは、平均、分散、共分散、および変動係数を計算する簡単な例を使って、各ステップについて見ていきましょう。
最初に新しいタスクを作成し、問題、次元 p、測定回数 n、およびデータセット X が格納されているメモリー位置をライブラリーの引数に渡す必要があります。
storage_format_x = VSL_SS_MATRIX_COLUMNS_STORAGE; errcode = vsldSSNewTask( &task, &p, &n, &storage_format_x, X, weights, indices );
配列 weights には、各測定値の重み付けが含まれており、配列 indices は処理する乱数生成のコンポーネントを決定します。例えば、indices は次のように初期化できます。
indices[p] = {0, 1, 1, 0, 1, ... };
つまり、乱数ベクトルの 0 番目と 3 番目のコンポーネントの測定は解析から除外されます。データセットは列形式でも行形式でも格納可能で、格納形式は変数 storage_format_x を使用して渡されます。すべての重み付けを 1 に設定して、乱数ベクトルのすべてのコンポーネントを処理する場合は、weights や indices の代わりに、NULL ポインターを渡します。
さらに、計算結果とほかの引数を保持するタスク・ディスクリプター配列を登録する必要があります。サマリー統計ライブラリーは、さまざまなエディターを提供しています。このアプリケーションでは、以下のエディターを使用しています。
errcode = vsldSSEditTask( task, VSL_SS_ACCUMULATED_WEIGHT, W ); errcode = vsldSSEditTask( task, VSL_SS_VARIATION_ARRAY, Variation ); errcode = vsldSSEditMoments( task, Xmean, Raw2Mom,0,0,Central2Mom, 0, 0); cov_storage = VSL_SS_MATRIX_FULL_STORAGE; errcode = vsldSSEditCovCor( task, Xmean, Cov, &Cov_storage , 0, 0);
平均、2 次代数積率、分散、変動係数の推定値は、Xmean、Raw2Mom、Central2Mom、Variation に格納されます。共分散の推定値は配列 Cov に格納されます。ライブラリーは計算結果の格納方法を “知っている” 必要があるため、サポートされているフルまたはパックド形式のいずれかを共分散行列の格納形式として必ず指定する必要があります。ほとんどの場合、平均の推定値が必要ない場合でも、それを格納する配列の登録が必要です。これは、平均値を使用するほかの多くの統計的推定値で必要になるためです (詳細は、ユーザーマニュアルを参照してください)。
これで任意の推定値を計算できます。計算ルーチンは一度だけ呼び出します。
errcode = vsldSSCompute( task,VSL_SS_MEAN | VSL_SS_2CENTRAL_MOMENT | VSL_SS_COVARIANCE_MATRIX | VSL_SS_VARIATION, VSL_SS_FAST_METHOD );
このライブラリーでは、データが格納されているメモリー位置へのライブラリー・ポインターを渡します。そうすることで、同じメモリー位置に別のデータを配置でき、タスク・ディスクリプターを再度編集しなくても Compute ルーチンを呼び出すことができます。
最後に、タスクに割り当てられているシステムリソースを解放します。
errcode = vslSSDeleteTask( &task );
p = 500、n = 100,000 の場合、上記の問題は 2 ウェイ構成のクアッドコア インテル® Xeon® プロセッサー E5440 2.8GHz (合計 8 コア) のシステムで 1.42 秒かかりました。同じアプリケーションをシリアルモードで (1 つのコアだけで) 実行した場合は、9.09 秒かかりました。
データをより小さなチャンク (塊) に分割して処理するには?
上記の章では、インテル® MKL のサマリー統計ライブラリーのツールを使用して、インメモリー・データセットの統計的推定値の計算方法について説明しました。私は前回と同じ統計的推定値を、今度はコンピューターのメモリーに格納しきれないデータを使って計算しなければならなくなりました。ここでは、データを処理するため、データセットをより小さなチャンクに分割します (一度に利用できないインメモリー・データでも、データを複数のチャンクに分割し、処理することができます)。今回もインテル® MKL のサマリー統計ライブラリーを利用することができるでしょうか? アプリケーションを大幅に変更しなくても、アウトオブメモリーのデータに対応できるでしょう。
前回と同様に、ライブラリーを使用するための 4 つのステップに従って作業を進めます。ただし、大規模なデータに対応するため、ここでは初期化を追加する必要があります。最初に、各推定値をゼロ (あるいはその他の適切な値) に初期化します。
for( i = 0; i < p; i++ )
{
Xmean[i] = 0.0;
Raw2Mom[i] = 0.0;
Central2Mom[i] = 0.0;
for(j = 0; j < p; j++)
{
Cov[i][j] = 0.0;
}
}
そして、重み付けの累積を格納するサイズ 2 の配列 W を初期化します。これは、推定値を正しく計算するために重要です。
W[0] = 0.0; W[1] = 0.0;
次に、データセットの最初のチャンクを配列 X に読み込み、観測値の重み付けを読み取ります。
GetNextDataChunk( X, weights );
そして、前回の記事で説明したステップと同様に、タスクの作成、引数の編集、必要な推定値の計算、タスクリソースの割り当て解除を行います。
/* タスクの作成 */
storage_format_x = VSL_SS_MATRIX_COLUMNS_STORAGE;
errcode = vsldSSNewTask( &task, &p, &n_portion, &storage_format_x, X, weights, indices );
/* タスク・パラメーターの編集 */
errcode = vsldSSEditTask( task, VSL_SS_ACCUMULATED_WEIGHT, W );
errcode = vsldSSEditTask( task, VSL_SS_VARIATION_ARRAY, Variation );
errcode = vsldSSEditMoments( task, Xmean, Raw2Mom, 0, 0, Central2Mom, 0, 0 );
Cov_storage = VSL_SS_MATRIX_FULL_STORAGE;
errcode = vsldSSEditCovCor( task, Xmean, (double*)Cov, &Cov_storage, 0, 0 );
/* データセットを分割したチャンクの推定値を計算 */
for( nchunk = 0; ; nchunk++ )
{
errcode = vsldSSCompute( task,
VSL_SS_MEAN | VSL_SS_2CENTRAL_MOMENT |
VSL_SS_COVARIANCE_MATRIX | VSL_SS_VARIATION,
VSL_SS_1PASS_METHOD );
If ( nchunk >= N ) break;
GetNextDataChunk( X, weights );
}
/* タスクリソースの割り当て解除 */
errcode = vslSSDeleteTask( &task );
さらに、データセットの次のチャンクを別の配列に格納することができます。全体の計算スキームは同じです。ただ単に、次のように、新しいチャンクの位置をライブラリーに知らせる必要があります。
for( nchunk = 0; ; nchunk++ )
{
errcode = vsldSSCompute( task,
VSL_SS_MEAN | VSL_SS_2CENTRAL_MOMENT | VSL_SS_COVARIANCE_MATRIX | VSL_SS_VARIATION,
VSL_SS_1PASS_METHOD );
If ( nchunk >= N ) break;
GetNextDataChunk( NextXChunk, weights );
errcode = vsldSSEditTask( task, VSL_SS_OBSERVATIONS, NextXChunk );
}
これだけです。簡単でしょう?
データセット内の外れ値を検出するには?
以前の章で、私はインテル® マス・カーネル・ライブラリー (インテル® MKL) のサマリー統計ライブラリーを使って、平均や分散共分散行列といったさまざまな統計的推定値を計算しました。そのときには、データセットに “不良な” 測定値 (測定した分布に属さない値) または外れ値が含まれていないことが分かっていました。
しかし、場合によっては、データセットに外れ値が含まれていることがあります。これは、マイクロアレイ技術による遺伝子発現レベルの測定のように、データ収集過程の信頼性が低いことが原因であったり、ネットワーク侵入のように意図的な行為の結果であったりします。どのような場合であっても、データセット内の外れ値は、偏った推定値や正しくない結論につながります。このようなデータセットはどのように処理したら良いでしょうか? インテル® MKL のサマリー統計ライブラリーの外れ値検出ツールを使ってみましょう。
このツールを検証するため、ここではインテル® マス・カーネル・ライブラリーのジェネレーターを使って多変量ガウス分布からデータを生成し、一部の測定値を、数学的期待値が非常に大きな多変量ガウス分布の測定値に置換し、外れ値の数は約 20% としました。それでは、サマリー統計ライブラリーの外れ値検出で BACON アルゴリズムがどのように外れ値を特定するのか見てみましょう。
以前の章で説明した、ライブラリーを使用する 4 つのステップについては、再度説明しません。ここでは、外れ値の検出方法において最も重要な点について述べます。アルゴリズムを使用する前に、引数を初期化しなければなりません。まず、アルゴリズムの初期化スキームを定義します。ライブラリーでは、中央値ベースのスキームとマハラノビス距離ベースのスキームという 2 つのオプションが提供されています。除外基準 alpha と停止基準 beta (各引数の詳細は、ライブラリーのマニュアルを参照してください) も定義する必要があります。以下のように定義できます。
init_method = VSL_SS_BACON_MEDIAN_INIT_METHOD; alpha = 0.05; beta = 0.005; BaconN = 3; BaconParams[0] = init_method; BaconParams[1] = alpha; BaconParams[2] = beta;
そして、次のように、ライブラリーの適切なエディターを使って、必要な引数を渡します。
errcode=vsldSSEditOutliersDetection(task, &BaconN, BaconParams, BaconWeights );
ここで使用している BaconWeights 引数は 重み付けの配列で、アルゴリズムの結果が格納され、疑わしい測定値を示します。この配列のサイズは測定値の数と同じになります。配列の i 番目の値が 0 の場合はその測定値には注意が必要なことを示し、1 の場合はその測定値は “問題ない” ことを示します。
次に、Compute 関数を呼び出します。
errcode = vsldSSCompute( task, VSL_SS_OUTLIERS_DETECTION, VSL_SS_BACON_METHOD );
アルゴリズムが完了すると、配列 BaconWeights には測定値の重み付けが格納されています。これを解析する必要があります。私が行ったテストでは、配列の中身を確認したところ、100% 正しい結果が得られました。つまり、すべての外れ値が正しく定義され、誤検出はありませんでした。この配列は今後の解析にも役立てることができます。測定値の重み付けの配列として登録し、通常の方法で使用することができます。外れ値を除外した後、私が偏っていない正しい統計的推定値を得られたことはいうまでもないでしょう。
マルチコアを活用しよう
これまでの章では、インテル® MKL のサマリー統計ライブラリーの機能と使用方法について説明しました。同様の機能を提供する統計パッケージはほかにも多数ありますが、インテル® MKL のサマリー統計ライブラリーを使うメリットはなんでしょう? それは、ほかにはない新しい機能や特別な機能があるからです。
新しい時代では、大きな次元の新しい問題が起こります。例えば、ヒトゲノムには少なくとも 30 億の DNA 塩基対があり、20,000 ~ 25,000 のタンパク質遺伝子があります。これは、処理するには非常に大きな情報量です。幸いなことに、マルチコア・プロセッサーを利用することで、このようなデータの配列処理が簡単になります。
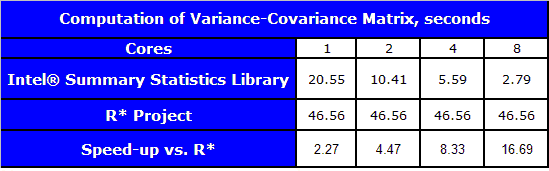
ライブラリーに含まれる重要な推定量の 1 つに、分散共分散行列の計算アルゴリズムがあります。このアルゴリズムを使って、サマリー統計ライブラリーが、同じ機能を備えたほかの一般的なライブラリーと比べてどの程度速いかを検証してみることにしました。比較には、GNU* R* プロジェクト 2.8.0 (データ処理用の関数群) の C で記述された共分散を推定するアルゴリズムを使用しました。パフォーマンスの測定は、2 ウェイ構成のクアッドコア インテル® Xeon® プロセッサー E5440 2.83 GHz、8GB RAM、2x6MB L2 キャッシュを搭載したマシンで行いました。利用可能なコアは 8 個で、omp_set_num_threads() 関数を使用して、測定で利用する最大コア数を設定しました。タスクの次元は 100、測定回数は 1,000,000 でした。データセットは多変量ガウス分布から生成し、分散共分散行列の計算には 1 パス処理を使用しました。利用可能なコア数が 8 の場合、サマリー統計ライブラリーは、R* のアルゴリズムよりも約 16.7 倍高速でした。
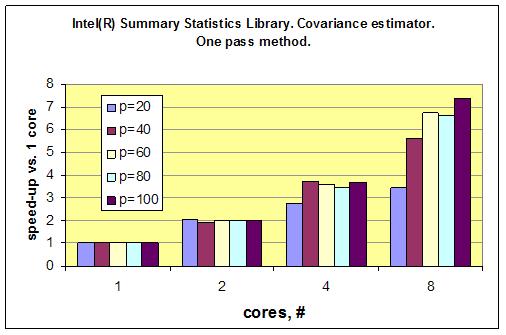
以下のグラフは、サマリー統計ライブラリーの共分散推定量が、コア数の増加に伴い優れたスケーリングを発揮することを示しています。それぞれの測定における測定回数は同じです。つまり、すべてのタスクの次元 (p=20、40、60、80、および 100) で測定回数は 1,000,000 です。一言でいえば、コア数が増えるにつれ、結果をより速く得られることが分かります。
アップデートで追加された新機能
インテル® MKL 10.3 のサマリー統計ライブラリー 1.0 のアップデートがご利用いただけます。このアップデートには、次の機能および利点が含まれています。
相関行列のパラメーター化アルゴリズム: 半正定性の特性を持たない入力を、相関行列の特性を満たす出力に変換します。このアルゴリズムは、スペクトル分解法に基づいており、財務計算で使用されます。
ストリーミング・データの分位数の計算アルゴリズム: 分位数の計算は、あらかじめ定義された確定された誤差を使って行われ、メモリーと速度の観点から非常に効率的です。このアルゴリズムは、ブロック単位で渡されるデータセットの処理に使用されます。
最適化されたデータセット内の外れ値の検出アルゴリズム: マルチコアシステムで利用可能なすべてのコアを効率良く活用します。
IA-32/インテル® 64 ベースの Windows* および Linux* プラットフォーム向けダイナミック・ライブラリー: サマリー統計ライブラリーは、アプリケーションのリンクにおいて柔軟性が向上しました。
サマリー統計ライブラリーは、多次元データセットの並列処理および解析ソリューションです。積率、歪度、尖度、変動係数、分位数/順序統計量の計算アルゴリズムに加えて、分散共分散行列の推定量が多数含まれています。また、データセット内の外れ値検出と欠測値サポートのためのロバスト手法とツールも提供します。ライブラリー・アルゴリズムの拡張セットにより、"プログレッシブ処理" サポート、つまりブロック単位で渡されるデータを解析することもできます。
ライブラリーのアルゴリズムは、マルチコア/SSE 対応プロセッサーをできるだけ活用します。
サマリー統計ライブラリーは、C および Fortran の API をサポートします。IA-32/インテル® 64 プラットフォーム向けの Windows*/Linux* 版は、http://software.intel.com/en-us/articles/intel-summary-statistics-library からダウンロードできます。
外れ値検出アルゴリズムはどの程度速いのか?
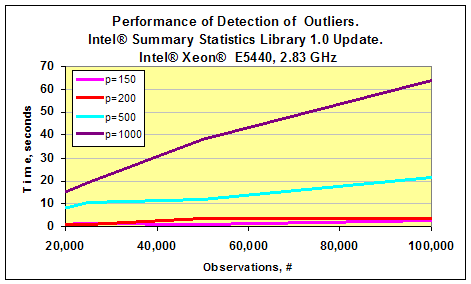
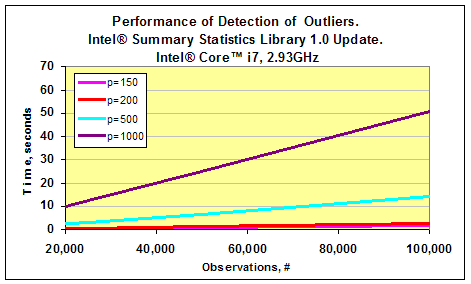
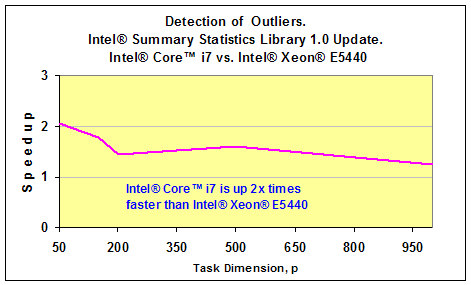
以前の章で 、インテル® MKL のサマリー統計ライブラリーの重要なコンポーネントであるデータセット内の外れ値の検出スキームについて説明しました。最近リリースされたサマリー統計ライブラリー 1.0 のアップデートには、このアルゴリズムの最適化バージョンが含まれています。 このアルゴリズムがどの程度速いのかを調査するため、私はインテル® Xeon® E5440 2.83 GHz とインテル® Core™ i7 2.93GHz ベースの 2 つのマシンでパフォーマンスを測定してみました。それぞれのテストでは、多変量ガウス分布からデータセットを生成しました。ガウスベクトルの次元 p は 50 から 1,000 までの値で、測定回数 n は 20,000 から 100,000 までの値でした。外れ値は、以前の記事で紹介したのと同様の方法で生成しました。以下の 2 つのグラフは、サマリー統計ライブラリー 1.0 のアップデートで利用可能な外れ値検出のパフォーマンスの測定結果です。p=50 の場合、アルゴリズムのパフォーマンスは 0.5 秒以下でした。これは、グラフには表示されていません。
タスクの次元 p が 1,000 で測定回数が 100,000 の場合、インテル® Core™ i7 プロセッサー・ベースのマシンでは処理全体にかかった時間は 1 分未満でした。インテル® Xeon® E5440 プロセッサー・ベースのマシンではもう少しかかりました。
つまり、このアプリケーションでは、インテル® Core™ i7 プロセッサーのほうが、インテル® Xeon® E5440 プロセッサーよりも 2 倍高速であるといえます。以下のグラフは、2 つのプラットフォームのパフォーマンスを比較した結果です。インテル® Core™ i7 プロセッサーのほうがクロック周波数がやや高いものの、外れ値検出アルゴリズムのスピードアップは格段に高いことが分かります。
ロバスト手法の使用方法
インテル® MKL のサマリー統計ライブラリーは、外れ値により “汚染された” データセットを処理する方法を提供します。以前の章で、データセット内の “疑わしい” 測定値の検出方法について説明しました。外れ値の検出アルゴリズムのパフォーマンスに関する考察は、こちらをご覧ください。外れ値を処理する別の方法として、ライブラリーでロバスト手法を利用できます。ここでは、特に注意が必要な平均および分散共分散行列のロバスト推定アルゴリズムの使用方法を説明します。
サマリー統計ライブラリーのロバスト手法は、Maronna[1] と TBS[2] の 2 つのアルゴリズムから成ります。1 つ目のアルゴリズムは、2 つ目のアルゴリズムの開始 “ポイント” (共分散と平均) の計算に使用されます。TBS アルゴリズムは、必要な精度が得られるか、最大反復回数に達するまで反復します。これらの引数に加えて、ライブラリーで最大降伏点 (アルゴリズムで許容可能な外れ値の数) と ARP (漸近の棄却率) を指定し、渡すことができます[2]。TBS アルゴリズムの反復を避け、Maronna アルゴリズムだけを使用して平均および共分散のロバスト推定を計算する場合は、反復数を 0 に設定します。
いつものように、サマリー統計ライブラリーを使用するには、タスクの作成、タスク引数の編集、統計的推定値の計算、リソースの割り当て解除から成る 4 つのステップに従って作業を進めます。この 4 つのステップについてはこちらで説明しているので、ここではロバスト手法のエディターと Compute ルーチンの使用方法だけを示します。アルゴリズムの引数である降伏点、ARP、精度と TBS 反復の最大数を配列で渡します。
breakdown_point = 0.2; arp = 0.001; method_accuracy = 0.001; iter_num = 5; robust_method_params[0] = breakdown_point; robust_method_params[1] = arp; robust_method_params[2] = method_accuracy; robust_method_params[3] = iter_num;
ロバスト推定を格納するメモリー t_est and cov_est も必要です。以下の例では、共分散行列は変数 robust_cov_storage で指定されたメモリー位置に通常の形式で格納されます。
errcode = vsldSSEditRobustCovariance( task, &robust_cov_storage, &robust_params_n, robust_method_params, t_est, cov_est );
推定値の計算は Compute ルーチンによって行われます。
errcode = vsldSSCompute(task, VSL_SS_ROBUST_COVARIANCE, VSL_SS_ROBUST_TBS_METHOD );
サマリー統計ライブラリーがどのように外れ値を処理するかを理解するため、次元 p = 10、測定回数 n = 10,000 のタスクを作成します。データセットは、平均が 0、主対角線上の要素が 1 で残りの要素が 0.5 の共分散行列の多変量ガウス分布から生成し、その後、同じ共分散行列と平均のベクトルがすべて 5 の多変量ガウス分布から生成した外れ値を含めます。
このデータセットに対して、ロバスト以外のアルゴリズムを使用して共分散および平均の推定値を計算すると、偏った結果になります。それぞれの推定値の p-value がゼロになっても驚くことではありません。
平均: 0.2566,0.2583,0.2576,0.2633,0.2439,0.2556,0.2530,0.2716,0.2535,0.2519
共分散: 2.2540 1.2715 2.1819 1.2852 1.2462 2.2046 1.2885 1.2684 1.2553 2.2310 1.2850 1.2581 1.2571 1.2526 2.2112 1.2650 1.2284 1.2419 1.2820 1.2430 2.1929 1.2789 1.2435 1.2550 1.2555 1.2574 1.2478 2.2113 1.2773 1.2692 1.2676 1.2751 1.2725 1.2733 1.2739 2.2448 1.2813 1.2579 1.2688 1.2723 1.2670 1.2713 1.2839 1.3061 2.2246 1.2696 1.2631 1.2515 1.2701 1.2597 1.2686 1.2554 1.2638 1.2780 2.1893
Maronna アルゴリズム (iter_num=0) を使用すると、次のような推定値となります。
平均: -0.0022,0.0081,-0.0075,0.0049,-0.0054,0.0012,-0.0087,0.0194,-0.0073,0.0022
平均の p-value: 0.1792 0.6077 0.5640 0.3869 0.4281 0.1014 0.6375 0.9570 0.5602 0.1846
共分散: 0.9164 0.0605 0.8945 0.0617 0.0374 0.9269 0.0602 0.0570 0.0472 0.9294 0.0584 0.0469 0.0599 0.0443 0.9183 0.0552 0.0394 0.0395 0.0655 0.0484 0.9049 0.0487 0.0449 0.0471 0.0451 0.0564 0.0461 0.9186 0.0293 0.0555 0.0539 0.0456 0.0450 0.0574 0.0501 0.9149 0.0507 0.0339 0.0433 0.0504 0.0429 0.0603 0.0597 0.0696 0.8962 0.0375 0.0573 0.0470 0.0472 0.0502 0.0607 0.0420 0.0381 0.0484 0.8848
共分散の p-value: 0.0000 0.2989 0.0000 0.2966 0.5842 0.0000 0.3471 0.4395 0.9592 0.0000 0.3994 0.9148 0.3590 0.8993 0.0000 0.5128 0.7023 0.6708 0.1869 0.8510 0.0000 0.8508 0.9752 0.9515 0.9411 0.4812 0.9714 0.0000 0.2669 0.4841 0.6001 0.9729 0.9530 0.4207 0.7751 0.0000 0.7151 0.4529 0.8765 0.7468 0.8689 0.2968 0.3317 0.0984 0.0000 0.6082 0.3734 0.9088 0.8997 0.7250 0.2720 0.8321 0.6358 0.7895 0.0000
先程よりも偏りの少ない推定値になりましたが、行列の主対角線の p-value はゼロのままです。より正確な推定値を得るため、TBS アルゴリズムの反復を 5 回実行してみます (これ以上反復回数を増やしても、推定値には大きな影響がないことは、簡単なテストを行えば分かります)。
平均: -0.0018,0.0034,0.0026,0.0067,-0.0108,0.0012,-0.0024,0.0122,-0.0057,-0.0044
平均の p-value: 0.1412 0.2612 0.2025 0.4860 0.7098 0.0943 0.1882 0.7693 0.4263 0.3381
共分散: 1.0524 0.0583 1.0172 0.0757 0.0426 1.0403 0.0653 0.0630 0.0490 1.0538 0.0672 0.0604 0.0559 0.0462 1.0367 0.0493 0.0295 0.0434 0.0784 0.0442 1.0261 0.0620 0.0429 0.0509 0.0453 0.0491 0.0488 1.0397 0.0410 0.0503 0.0476 0.0507 0.0497 0.0514 0.0497 1.0367 0.0450 0.0370 0.0486 0.0464 0.0430 0.0526 0.0622 0.0719 1.0179 0.0477 0.0587 0.0461 0.0562 0.0514 0.0645 0.0443 0.0346 0.0485 1.0070
共分散の p-value: 0.0002 0.6951 0.2249 0.1676 0.5972 0.0044 0.4613 0.5057 0.8450 0.0001 0.3761 0.5862 0.8152 0.7231 0.0095 0.8726 0.1942 0.6233 0.1170 0.6604 0.0646 0.5690 0.6118 0.9464 0.6795 0.8671 0.8653 0.0050 0.5092 0.9507 0.7992 0.9266 0.9002 0.9932 0.8944 0.0094 0.6867 0.4013 0.8656 0.7504 0.6147 0.9305 0.5185 0.2177 0.2065 0.8205 0.6243 0.7594 0.7800 0.9869 0.4071 0.6776 0.3207 0.8961 0.6185
参考文献 (英語)
1. R.A. Maronna and R.H. Zamar, Robust Multivariate Estimates for High-Dimensional Datasets. Technometrics, 44, 307–317, 2002.
2. David M. Rocke. Robustness properties of S-estimators of multivariate location and shape in high dimension. The Annals of Statistics, 24(3), 1327-1345, 1996.
欠測値の処理方法
実際のデータセットには欠測値が含まれていることがあります。欠測値をどのように処理すべきかという課題に直面する例として、複雑な生態系の社会学的な調査と測定が挙げられます。また、データセット内の外れ値は欠測値として扱うこともできます。インテル® MKL のサマリー統計ライブラリーには、“疑わしい” 測定値がある場合に外れ値を検出したり、ロバスト推定を行う機能が備わっています。これらのアルゴリズムの使用法については以前の記事で説明しました。ここでは、サマリー統計ライブラリーに含まれる欠測値を処理する機能ついて説明します。
欠測値を含むデータセットを正しく処理するには、[1] のアプローチを使用します。期待値最大化 (EM) とデータ拡大 (DA) アルゴリズムは、このソリューション (ここでは EMDA ソリューションと呼びましょう) に不可欠な要素です。このソリューションは m セットのシミュレートされた欠測値を出力します。この欠測値のセットをデータセットに含め、m 個の完全なデータのコピーを作成できます。各データセットに対して統計的推定値を計算し、m 個の推定値をまとめて最終的な推定値が得られます。
EMDA ソリューションを使用するには、こちらで説明しているライブラリーのその他のアルゴリズムと同様に、タスクの作成、引数の編集、推定値の計算、リソースの割り当て解除を行います。以下に EMDA ソリューションからライブラリーに引数を渡し、Compute ルーチンを呼び出す方法を説明します。
EM アルゴリズムは em_iter_num 回反復して、平均および共分散の初期推定値を計算します。この推定値は DA アルゴリズムで使用されます。指定された精度 em_accuracy が達成されると、EM アルゴリズムは指定された反復回数を実行していなくても終了します。EM アルゴリズムが終了すると、DA アルゴリズムは da_iter_num 回反復します。このアルゴリズムはガウス乱数を使用するため、サマリー統計ライブラリーはインテル® マス・カーネル・ライブラリーのベクトル・スタティスティカル・ライブラリー (VSL) を使用します。BRNG、SEED、および METHOD は VSL ジェネレーターの初期化に使用される引数です。引数の値は VSL の必要条件を満たしていなければなりません。EMDA ソリューションでは欠測値の数 missing_value_num も必要になります。欠測値の数を計算するには、データセットを事前に処理し、ライブラリーで定義されているマクロ VSL_SS_DNAN (単精度浮動小数点算術演算の場合は VSL_SS_SNAN) を使用して欠測値をマークします。アルゴリズムの引数はライブラリーに配列で渡します。
em_iter_num = 10; da_iter_num = 5; em_accuracy = 0.001; copy_num = m; miss_value_num = miss_num; brng = BRNG; seed = SEED; method = METHOD; mi_method_params[0] = em_iter_num; mi_method_params[1] = da_iter_num; mi_method_params[2] = em_accuracy; mi_method_params[3] = copy_num; mi_method_params[4] = missing_value_num; mi_method_params[5] = brng; mi_method_params[6] = seed; mi_method_params[7] = method;
EMDA アルゴリズムのエディターは引数のセットを受け付けます。
errcode = vsldSSEditMissingValues(task, &mi_method_params_n, mi_method_params, &initial_estimates_n, initial_estimates, &prior_n, prior, &simulated_missing_values_n, simulated_missing_values, &estimates_n, estimates);
配列 mi_method_params は上記に示すとおりです。EM アルゴリズムは初期推定値の配列 initial_estimates を使用して開始します。最初の p 項目には平均のベクトルが格納され、残りの p*(p+1)/2 項目には分散共分散行列の上三角の部分が格納されます (p はタスクの次元)。配列 prior は EMDA アルゴリズムの以前の引数を格納します。ライブラリーの現在のバージョンではユーザー定義の prior をサポートしていないため、デフォルト値が使用されます。
シミュレートされた欠測値のセットは配列 simulated_missing_values で返され、合計 m x missing_value_num 個の値になります。欠測値は、最初に乱数ベクトルの第 1 変数のすべての欠測値、次に第 2 変数のものという順に 1 つずつ格納されます。DA アルゴリズムの収束を推定するには、すべての反復の平均/共分散とすべてのシミュレートされた欠測値 ( 合計 m x da_iter_num x ( p + 0.5 x (p2 + p) ) 個) を格納した配列 estimates を渡します。各推定値のセットは上記のように格納されます - 最初の p 項目には平均が、残りの 0.5 x (p2 + p) 項目には共分散行列の上三角の部分が格納されます。
最後に、ライブラリーの Compute ルーチンを使用して EMDA アルゴリズムを実行します。
errcode = vsldSSCompute(task,VSL_SS_MISSING_VALUES,SL_SS_MULTIPLE_IMPUTATION);
このソリューションの動作を理解するため、次元 p = 10、測定回数 n = 10,000 のタスクを作成し、平均が 0、主対角線上の要素が 1 で残りの要素が 0.05 の共分散行列の多変量ガウス分布からデータセットを生成しました。データセット内の欠測値の割合は 10% で、各測定のどこかに欠測値が 1 つ含まれている可能性があります。シミュレートされた欠測値のセットは 100 (m=100) 生成しました。EM アルゴリズムの開始 "ポイント" は、平均が 0 で同一の共分散行列のベクトル、つまり配列 prior へのポインターは 0 (そして、この配列のサイズ prior_n も 0) に設定しました。
最初に da_iter_num = 10 で実行し、配列 estimates の推定値を解析してみました。その結果、DA アルゴリズムの反復回数を 5 回減らせることが分かりました。次に、欠測値 100 セットのシミュレーションを行い、シミュレートされた値をデータセットに含め、100 個の完全な配列を作成しました。そして完全なデータセットごとに、インテル® MKL のサマリー統計ライブラリーを使って平均と分散を計算し、合計 100 セットの平均と共分散の推定を得ました。
Set: Mean: 1 0.013687 0.005529 0.004011 ... 0.008066 2 0.012054 0.003741 0.006907 ... 0.003721 3 0.013236 0.008314 0.008033 ... 0.011987 ... 99 0.013350 0.012816 0.012942 ... 0.004076 100 0.014677 0.011909 0.005399 ... 0.006457 ____________________________________________________ Average 0.012353 0.005676 0.007586 ... 0.006004
Set: Variance: 1 0.989609 0.993073 1.007031 ... 1.000655 2 0.994033 0.986132 0.997705 ... 1.003134 3 1.003835 0.991947 0.997933 ... 0.997069 ... 99 0.991922 0.988661 1.012045 ... 1.005406 100 0.987327 0.989517 1.009951 ... 0.998941 ____________________________________________________ Average 0.99241 0.992136 1.007225 ... 1.000804
Between-imputation variance: 0.000007 0.000008 0.000008 ... 0.000007
Within-imputation variance: 0.000099 0.000099 0.000101 ... 0.000100
Total variance: 0.000106 0.000107 0.000108 ... 0.000108
平均のベクトルを 95% 信頼区間でも計算してみました。
95% confidence interval: Right boundary of interval: +0.032939 +0.026372 +0.028406 ... +0.026744 Left boundary of interval: -0.008234 -0.015020 -0.013233 ... -0.014736
さらに、EMDA アルゴリズムを評価するため、同じテストを 20 回繰り返してみました。その結果、95% 信頼区間で行った 20 回すべてのテストで正しい平均値を得ることができました。素晴らしいことだと思いませんか?
参考文献 (英語)
1. J.L. Schafer. Analysis of Incomplete Multivariate Data, Chapman & Hall/CRC, 1997.