インテル® MKL の BLAS と DGEMM ルーチンを使用したインテル® AVX の最適化

この記事は、インテル® ソフトウェア・ネットワークに掲載されている「Optimize for Intel® AVX Using Intel® Math Kernel Library’s Basic Linear Algebra Subprograms (BLAS) with DGEMM Routine」(http://software.intel.com/en-us/articles/optimize-for-intel-avx-using-intel-math-kernel-librarys-basic-linear-algebra-subprograms-blas-with-dgemm-routine/) の日本語参考訳です。

はじめに

インテル® マス・カーネル・ライブラリー (インテル® MKL) は、科学エンジニアリング分野で使用できる広範囲な機能セットを提供しています。以下に、主な機能を示します。

• 線形代数 – BLAS (Basic Linear Algebra Subprograms)、LAPACK、ScaLAPACK、スパース BLAS、反復法スパースソルバー、前処理、直接法スパースソルバー (PARDISO)
• FFT – シーケンシャル FFT とクラスター FFT
• 統計 – ベクトル統計ライブラリー (VSL) と乱数ジェネレーター
• ベクトル演算 – ベクトル・マス・ライブラリー (VML)
• PDE – ポアソン、ヘルムホルツ・ソルバー、三角変換
• 最適化 – Trust Region ソルバー

この記事では、インテル® MKL の概要、DGEMM に関連する拡張とパフォーマンス、いくつかの新しいインテル® アドバンスト・ベクトル・エクステンション (インテル® AVX) 命令について説明します。DGEMM は、倍精度行列の乗算アルゴリズムで、BLAS の重要なルーチンです。DGEMM の詳細は、次のセクションで定義します。DGEMM は線形代数の基本的なルーチンであるため、まず最適化を行うことにしました。

インテル® MKL の多くの機能は、ライブラリーが容易に利用できるように設計されています。いくつかのルーチンについては、柔軟性のために、異なるインターフェイスが提供されています (例えば、BLAS の C インターフェイスや LAPACK の FORTRAN 90 インターフェイス)。

インテル® MKL は、可能な限りコンパイラーに依存しないように設計されており、コンポーネントは独立したライブラリー・レイヤーで分けられています。インテル® コンパイラーのスレッドレイヤーだけでなく、GNU コンパイラーのスレッドレイヤーもあります。コードはいずれかのレイヤーとリンクでき、インテル® コンパイラーまたは GNU コンパイラーに依存するルーチンは各レイヤーに分離されます。図 1 は、インテル® MKL のレイヤーモデルを示しています。詳細は、参考文献 [1] で示す URL を参照してください。

インテル® MKL を使用する開発者は、プロセッサーのチューニングについて心配する必要はありません。インテル® MKL のライブラリーはプロセッサー・ディスパッチ機能を持ち、実行時にそのプロセッサーで最適なルーチンが使用されます。例えば、インテル® Xeon® プロセッサー 5400 番台で動作する 64 ビット Windows* 上で、BLAS を使用するアプリケーションをインテル® AVX 対応のインテル® MKL とリンクして、同じバイナリーをインテル® AVX 対応のインテル® プロセッサー上で実行すると、異なるプロセッサー向けに異なるコードがディスパッチされます。つまり、同じバイナリーを両方のランタイム環境で使用できます。インテル® MKL を使用すると、開発者は異なるプロセッサー向けに別々のバイナリーを用意することなく、常に最高のパフォーマンスが得られます。

インテル® MKL は、互換プロセッサーでも優れたパフォーマンスを実現するため、開発者は製品に 1 つのライブラリーを使用するだけでかまいません。

インテル® MKL はスレッドセーフで、スレッド化とマルチコアの最適化もサポートしています。インテル® MKL でリンクを行うことで、開発者はスレッド化に適した箇所のパフォーマンスを向上させることができます。

図 1: インテル® MKL のレイヤーモデル

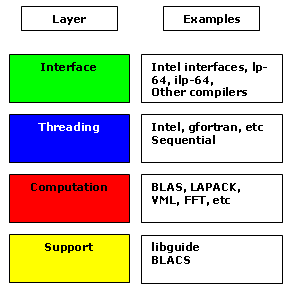
DGEMM と BLAS の詳細を説明した後、DGEMM の実装でインテル® AVX を活用する方法を示します。

DGEMM と BLAS

BLAS は Basic Linear Algebra Subprograms [2] の略で、インテル® AVX での実装を試みた最初の 3 つの機能コンポーネントの 1 つです。今後は、インテル® MKL のほかのコンポーネントとルーチンでも実装を試みる予定です。これまで 3 つのコンポーネント (BLAS、FFT、VML) で実装の試みが完了していますが、この記事では BLAS についてのみ説明します。BLAS は多くの線形代数ルーチンの基本的なビルディング・ブロックであるため、まずは BLAS から開始しました。

BLAS の本来の目的は、一般的な線形代数ルーチンを使用する開発者がベンダーによってチューニングされたライブラリーを活用できるように、ユニバーサルな API を作成することでした。インテル® MKL は、この考え方のさらに先を行くもので、BLAS を使用する開発者は、インテル® AVX のような新しいインテルの拡張機能を活用できるだけでなく、自動的にプロセッサーを確認して、プロセッサー固有の最適化を利用するバイナリーを作成することができます。

つまり、インテル® MKL を使用して作成されたバイナリーは、インテル® AVX に対応するプロセッサー上ではインテル® AVX コードをディスパッチし、その他のプロセッサー上ではインテル® SSE2 コードをディスパッチします。そのため、予備コードでビルドしたバイナリーは、現在のプロセッサー上でも、インテル® AVX のような将来の拡張をシミュレーションして問題なく実行できます。プロセッサー固有の最適化処理が考慮されるため、開発者はこれについて心配する必要はありません。

BLAS は、1 から 3 の「レベル」に分類されます。表 1 は BLAS の特徴を要約したものです (N はベクトルサイズまたは行列の次数)。レベルの数値は浮動小数点演算の桁で定義されますが、データ移動と浮動小数点演算の比率はレベル 3 BLAS が最も適していることに注意してください。

表 1. BLAS のレベル

メモリーのパフォーマンスと近年のプロセッサーの計算速度の差は広がるばかりです。これは、高速なメモリーは高価であり、大量に実装することが困難なためです。この状況は何年も続いており、回避策としては、メインメモリーに複数のキャッシュ階層を備えたマルチコアマシンを構築することが挙げられます。この階層の異なるレベルを活用するため、アルゴリズムにデータ・ブロッキングを取り入れます。

メモリー階層をピラミッドにすると [3]、図 2 のようになります。ピラミッドの上部には最も高速で最も小さいメモリーが含まれ、ピラミッドの下部には最も低速で最も大きなメモリーが含まれます。このピラミッドを利用するのに最も適しているルーチンは、レベル 3 BLAS です。レベル 3 BLAS が最も適している理由は、メモリー・インタラクション (相互作用) よりも計算の桁が多いことです。メモリー・インタラクションは、ピラミッドのさまざまな段階を有効に利用するように構成されます。

ただし、ピラミッドの概念を現代のマルチコアの最適化に完全に当てはめることはできません。その違いは、マルチコアでは、多くのコアはピラミッドの上部にあり、コア間の共有キャッシュがあることです。ピラミッドの下部には NUMA (Non-Uniform Memory Access) ベースのモデルも含まれます。

最も高いレベルはマシンのレジスターであると考えます。レジスターのデータ移動は、プロセッサーのクロックレートと同じ速さで行われます。次のレベルはデータ・キャッシュ・ユニット (DCU) で、次が中間レベルキャッシュ、その次が最終レベルキャッシュ、そして最後がメインメモリーです。すべてのメモリーはすべてのプロセッサーからアクセスできますが、一部のメモリーは一部のプロセッサーからのアクセスがほかのプロセッサーよりも速いため、メモリーアクセスのコストは異なります (NUMA の場合)。

図 2: メモリー階層ピラミッド

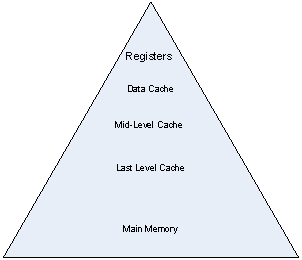
ピラミッドの上になるほど、リソースの価値は高くなります。理想的な環境では、(特に階層のあるレベルでミスがあると) メモリーの移動が遅くなるため、メモリーの移動よりも flops のほうが高くなります。レベル3 BLAS ルーチンの flops は O(N^3) でデータ移動は O(N^2) であるため、すべてのレベルのメモリー階層をブロックすることが可能です。

前述したように、マルチコアおよび NUMA は図 2 とは少し異なります。特に、各コアには個別のデータキャッシュと中間レベルキャッシュがありますが、最終レベルキャッシュはコア間で共有されます。最終レベルキャッシュには中間レベルキャッシュが含まれることがありますが、中間レベルキャッシュにはデータキャッシュは含まれません。

図 3: DGEMM の異なる操作

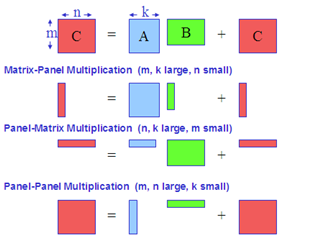
一連のステップとしてメモリー階層を見てみましょう。任意の時点で、あるステップのデータは、別のステップで階層の上または下に移動する必要があります。[6] で最も重要な点は、メモリー階層の任意のステップでは、ほかのステップを無視して、次のステップに進むために必要なデータ移動のオーバーヘッドが最小になるように、可能な限り適切にブロッキングの選択に注目することができるという所見です。これは、全体的な問題を解決するために最も速い手法を選択できるという、アルゴリズムの集合につながります。

インテル® MKL では、同様のアプローチを使用しています。この種のアプローチは [7] のような最近成功した事例でも使用されています。

DGEMM とインテル® AVX

インテル® AVX のレジスター幅は、インテル® SSE2 レジスターの倍です。インテル® MKL 内の DGEMM カーネルの多くは、以下の 3 つの命令で構成されます。

• vmovaps
• vaddp
• vmulpd

これらの命令は、以下のインテル® SSE2 命令を拡張したものです。

• movaps
• addpd
• mulpd

つまり、2 つの倍精度要素を 128 ビットのインテル® SSE2 レジスターで処理する代わりに、4 つの倍精度要素を 256 ビットのインテル® AVX レジスターで処理することができます。最新のインテル® Core™2 ハードウェア上でインテル® SSE2 命令を実行する場合、プロセッサーは addpd と mulpd を同時に (異なるポートで) 実行できることに注意してください。これは、インテル® Core™2 ハードウェアでは、ピークの浮動小数点レートが 1 サイクルあたり 4 浮動小数点演算である (addpd で 2 つの倍精度を加算し、mulpd で 2 つの倍精度を乗算する) ことを意味します。単精度演算の数はこの倍になりますが、この記事では倍精度に注目します。

インテル® AVX は、理論的な浮動小数点のバンド幅を倍にします。これは、インテル® AVX のハードウェア実装は同じサイクルでさらに vaddpd と vmulpd を実行できるためです。ただし、レジスター幅も同様に 2 倍になるため、理論的な浮動小数点レートは 2 倍になります。もちろん、vmovaps からのレジスター移動レートも 2 倍になります。

このほかに便利な命令として、vbroadcastsd があります。この命令は、インテル® AVX レジスターの 4 つの 64 ビットすべてに同じ値をロードします。

インテル® AVX の多くの命令では、3 つ目のデスティネーション・パラメーターを指定できるため、インテル® SSE2 命令よりも高い柔軟性が提供されます。例えば、”vmulpd ymm0, ymm1, ymm2″ を実行した後、異なる命令で同じ入力パラメーターを再利用できます (デスティネーション・レジスターは Windows* では最初のレジスター ymm0 で、Linux* では最後のレジスター ymm2 ですが、最初の確認は Windows 上で行ったため、この記事の命令はすべて Windows の構文を使用しています)。インテル® SSE2 では、後のステップで使用するレジスターを格納するために、追加のレジスター移動命令が必要です。

パフォーマンスのシミュレーションでは、インテル® AVX コードのパフォーマンスは同様のインテル® SSE2 コードのほぼ 2 倍になることが分かりました。

データがキャッシュに含まれていて何も問題 (バンク競合、TLB、キャッシュミスなど) がない場合、1 サイクルあたりおよそ 32 バイト (256 ビット、1 拡張レジスター) をロードできます。キャッシュをブロックできるように、レジスターをブロックできます (レジスター・ブロッキング)。vaddpd と vmulpd を同時に行うと 1 サイクルあたり 512 ビットのデータを処理できるため、レジスター・ブロッキングを仮定しています。これは、データをロードするよりも速く計算できることを意味します。このため、レジスター・ブロッキングから再利用が行われるように (A または B からのロードが C の一時計算中にできるだけ再利用されるように) します。

レジスター・ブロッキングを説明するため、ブロッキングが行われていない DGMM 内部カーネルの例を最初に考えてみましょう。前述したように、新しいインテル® AVX レジスターは 4 つの 64 ビット浮動小数点値を保持できます。それぞれ 1 つのレジスターで A からのロード、B からのロード、4 つの内積の蓄積を行う場合、コードは以下のようになります。

vmovapd ymm0, [rax]

vbroadcastsd ymm1, [rbx]

vmulpd ymm0, ymm0, ymm1

vaddpd ymm2, ymm2, vmm0

ここでは、rax が A のアドレス、rbx が B のアドレスを含んでいると仮定します。一度に 1 つの B 値のみを取得して、4 つの異なる A 値を掛けていることに注目してください。A 値にレジスター ymm0、B 値にレジスター ymm1、C 値にレジスター ymm2 を使用しています。rax と rbx が適切にインクリメントされ、ループカウントが作成されたら、ループの最後で、A*B の 4 つの行は完了です。このコードはレジスター・ブロッキングを行っていません。このコードの問題は、加算と乗算のペアごとに 2 回のロードが行われることです。加算と乗算は 1 つのサイクルでともに実行できますが、A と B のロードは 1 サイクルよりも多く必要なため、ループはロードにより制限を受けることになります。

レジスター・ブロッキングが行われるように、この手法を拡張してみましょう。拡張した手法では、A のロードごとに 1 つのレジスターが必要です。(ブロードキャストを使用している場合でも) B のロードごとに 1 つのレジスターが必要です。ここで、α が A のロードを行うレジスター数であると仮定します。また、β が B のロードを行うレジスター数であると仮定します。この手法では、C の内積を格納するために少なくとも αβ 個のレジスターが必要になります。使用するレジスター数の合計は α + β + αβ ですが、 乗算または加算に使用するレジスター数は αβ です。

ここでの目的は、合計で 16 個というレジスター数の制限に従いつつ、ロードと比較してできるだけ多くのレジスターを加算と乗算に使用することです。ロードの数は α + β です。この場合、可能性のあるソリューションは (α=4,β=2)、(α=2,β=4)、または (α=3,β=3) です。いずれの場合も、A と B のロードに使用したレジスターを再利用することで、最初の例とは異なるように内部ループを構成し、ロードよりも多くの乗算と加算を行うことができます。

この形式のレジスター・ブロッキングは単に最内ループのアンロールと見ることもできます。アンロールの因数が決定されたら、あとは計算の順序を決定するだけです。インテル® MKL は、レジスター、キャッシュ、TLB をブロックしますが、考慮すべき点はほかにもあります。例えば、DCU には 8 つのメモリーバンクがあるため、ともに同じバンクにアクセスしないようにします。ほかにできることは、後で必要になる値のプリフェッチです。プリフェッチ命令の形式はさまざまです。最も単純なのは、必要になる前にレジスターに値をロードする形式です。もちろん、プロセッサーはアウトオブオーダー実行を行いますが、このためには多くのリソースを管理する必要があります。最内ループは完全にアンロールされると非常に長くなりますが、多くの場合、リソースの管理を支援することになります。

レジスター・ブロッキングでは、乗算と加算の数と比較したロードとストアの数を最小化しようとしました。DGEMM (C = C + A*B; C は MxN、A は MxK、B は KxN) では、アプリケーションで頻繁に使用される M と N の両方が K よりもはるかに大きいときにパフォーマンスが高くなることが重要です。新しい DGEMM では、事前シミュレーターによるシミュレーションで、M=N=1024 および K=128 のケースをテストしました。理論上は、既存のハードウェアではクロックの半分で実行されます。シミュレーションによれば、このケースではパフォーマンスが 1.9 倍向上しました。

まとめ

インテル® AVX を使用してインテル® MKL の 3 つの機能を最適化したところ、その結果は非常に満足できるものでした。インテル® SSE2 の命令を拡張した新しい命令を使用することで、理論的な浮動小数点の能力が 2 倍になることを確認しました。例えば、最も重要な BLAS 関数である DGEMM でも同様の結果が得られました。このカーネルでは、行列がデータ・キャッシュ・ユニットに収まる場合、インテル® SSE2 コードのほぼ 2 倍のパフォーマンスが得られます。

インテル® MKL には、今後もより多くのインテル® AVX を使用した最適化が追加されます。インテル® AVX に対応するプロセッサー上ではインテル® AVX 命令が自動的にディスパッチされ、その他のプロセッサー上では既存の高品質なインテル® MKL コードがディスパッチされます。

参考文献 (英語)

• Intel Performance Libraries: Multicore-ready Software for Numeric Intensive Computation, by I. Burylov, M. Chuvelev, B. Greer, G. Henry, S. Kuznetsov, B. Sabanin, Intel Technical Journal, Q4 Vol. 11 Issue 4, November 2007, http://www.intel.com/technology/itj/2007/v11i4/4-libraries/1-abstract.htm
• A Set of Level 3 Basic Linear Algebra Subprograms, by J.J. Dongarra, J. Du Croz, I.S. Duff, and S. Hammarling, TR ANL-MCS-TM-88, Argonne National Laboratory, Argonne, IL, 1988.
• Matrix Computations, by G.H. Golub and C. Van Loan, The Johns Hopkins University Press, Baltimore MD, 2nd Ed., 1989.
• GEMM-based Level 3 BLAS, by B. Kågström and C. Van Loan, TR CTC91TR47, Cornell Theory C enter, Ithaca NY 1991.
• FLAME: Formal Linear Algebra Methods Environment, by John A. Gunnels, Fred G. Gustavson, Greg M. Henry, and Robert A. van de Geijn, ACM Transactions on Mathematical Software, Volume 27, No. 4, Pages 422-455, Dec. 2001.
• High-Performance Matrix Multiplication Algorithms for Architectures with Hierarchical Memories, by John A. Gunnels, Greg M. Henry, and Robert A. van de Geijn, FLAME Working Note #4, June 2001.
• Anatomy of High Performance Matrix Multiplication, by Kazushige Goto and Robert van de Geijn, ACM Transactions on Mathematical Software, Vol 34, No 3, 2008.

著者紹介

Greg Henry は、インテル社のソフトウェア & ソリューション・グループの開発製品部門 (インテル® MKL チーム) の主任エンジニアで、インテル® MKL に関連する線形代数、並列コンピューティング、数値解析、科学技術計算科学などの研究を行っています。Cornell University で応用数学の博士号を取得した後、1993 年 8 月にインテルに入社しました。趣味として小説の執筆も行っています。

編集部追加

本記事でも述べられているように、インテル® MKL を利用することは、最新プロセッサーの性能を引き出すための最も簡単な解決法の１つです。以下のリリースノート（英語）には、アップデートごとに着々と各関数ドメインのパフォーマンスが向上していることが記されています。
http://software.intel.com/en-us/articles/intel-mkl-103-release-notes/

計算処理の高速化を課題とされている方は、クラスター・アプリケーションにも対応可能なインテル® MKL を是非ともお試しください。評価版のダウンロード、お問い合わせはエクセルソフト株式会社まで。