この記事は、インテル® ソフトウェア・ネットワークに掲載されている「Intel® AVX Realization Of IIR Filter For Complex Float Data」(http://software.intel.com/en-us/articles/intel-avx-realization-of-iir-filter-for-complex-float-data/) の日本語参考訳です。
はじめに
インテル® AVX 命令を使用した complex float データ型の IIR フィルターの実装
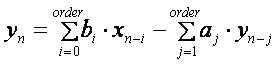
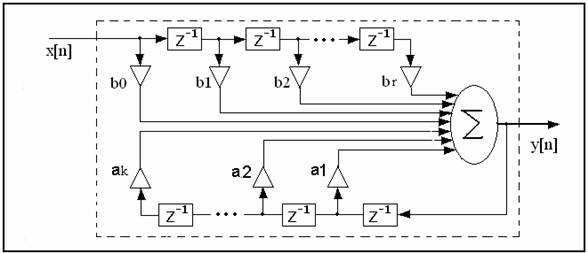
この手法はほかのデータ型 (例えば、特定のベクトル要素の real データ型や double データ型) にも適用することができます。以降の説明では complex float データ型を対象にしています。つまり、以下の加算、減算、乗算はすべて複素数演算です。ここでの目標は、”a” 係数を再計算して 4 つの “y” 計算をベクトル化 (してフィードバックの遅延を排除) することです。方程式 1 は次のように表現できます。
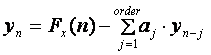
b0.re, b0.re, b0.re, b0.re, b0.re, b0.re, b0.re, b0.re -b0.im, b0.im,-b0.im, b0.im,-b0.im, b0.im,-b0.im, b0.im b1.re, b1.re, b1.re, b1.re, b1.re, b1.re, b1.re, b1.re -b1.im, b1.im,-b1.im, b1.im,-b1.im, b1.im,-b1.im, b1.im ………………….. bk.re, bk.re, bk.re, bk.re, bk.re, bk.re, bk.re, bk.re -bk.im, bk.im,-bk.im, bk.im,-bk.im, bk.im,-bk.im, bk.im
Load YMM reg = {x3.im, x3.re, x2.im, x2.re, x1.im, x1.re, x0.im, x0.re}
vmulps {bk.re, bk.re, bk.re, bk.re, bk.re, bk.re, bk.re, bk.re}+
Vshufps YMM reg = {x3.re, x3.im, x2.re, x2.im, x1.re, x1.im, x0.re, x0.im}
vmulps {-bk.im, bk.im,-bk.im, bk.im,-bk.im, bk.im,-bk.im, bk.im}
+…………………………………………………………………………………………………………………
…………………………………………………………………………………………………… +
Load YMM reg = {x3+k.im, x3+k.re, x2+k.im, x2+k.re, x1+k.im, x1+k.re, xk.im, xk.re}
vmulps {b0.re, b0.re, b0.re, b0.re, b0.re, b0.re, b0.re, b0.re} +
Vshufps YMM reg = {x3+k.re, x3+k.im, x2+k.re, x2+k.im, x1+k.re, x1+k.im, xk.re, xk.im}
vmulps {-b0.im, b0.im,-b0.im, b0.im,-b0.im, b0.im,-b0.im, b0.im} = Fx(n+0).re,im, Fx(n+1).re,im, Fx(n+2).re,im, Fx(n+3).re,im
//デスティネーション・ベクトルに一時的に格納します。
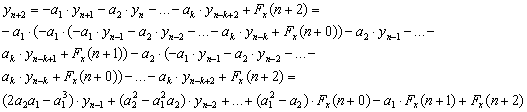
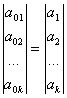
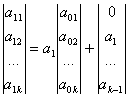
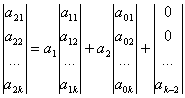
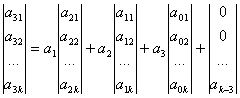
- a0n – バンドルの最初のポイント – 方程式 6
- a1n – バンドルの 2 つ目のポイント – 方程式 7
- a2n – バンドルの 3 つ目のポイント – 方程式 8
- a3n – バンドルの 4 つ目のポイント – 方程式 9
|
1.
|
0,
|
0,
|
0,
|
1;
|
|
2.
|
a01,
|
0,
|
0,
|
1;
|
|
3.
|
a11,
|
a01,
|
0,
|
1;
|
|
4.
|
a21,
|
a11,
|
a01,
|
1;
|
a01.re,im, a11.re,im, a21.re,im, a31.re,im a02.re,im, a12.re,im, a22.re,im, a32.re,im ................... a0k.re,im, a1k.re,im, a2k.re,im, a3k.re,im 0.re,im, a01.re,im, a11.re,im, a21.re,im 0.re,im, 0.re,im, a01.re,im, a11.re,im 0.re,im, 0.re,im, 0.re,im, a01.re,im
vbroadcast to YMM = {yn-1.re, yn-1.re, yn-1.re, yn-1.re,yn-1.re, yn-1.re, yn-1.re, yn-1.re}
vmulps {a01.re, a01.im, a11.re, a11.im, a21.re, a21.im, a31.re, a31.im} +
vbroadcast to YMM = {yn-1.im, yn-1.im, yn-1.im, yn-1.im,yn-1.im, yn-1.im, yn-1.im, yn-1.im}
vmulps {a01.im, a01.re, a11.im, a11.re, a21.im, a21.re, a31.im, a31.re} +
……………………………… +
vbroadcast to YMM = {yn-k.re, yn-k.re, yn-k.re, yn-k.re,yn-k.re, yn-k.re, yn-k.re, yn-k.re}
vmulps {a0k.re, a0k.im, a1k.re, a1k.im, a2k.re, a2k.im, a3k.re, a3k.im} +
vbroadcast to YMM = {yn-k.im, yn-k.im, yn-k.im, yn-k.im,yn-k.im, yn-k.im, yn-k.im, yn-k.im}
vmulps {a0k.im, a0k.re, a1k.im, a1k.re, a2k.im, a2k.re, a3k.im, a3k.re} +
vbroadcast to YMM = { Fx(n+0), Fx(n+0), Fx(n+0), Fx(n+0)}re.im
vmulps { a0k.re,im, a1k.re,im, a2k.re,im, a3k.re,im } + (extra)
vbroadcast to YMM = { Fx(n+1), Fx(n+1), Fx(n+1), Fx(n+1)}re.im
vmulps { 0.re,im, a01.re,im, a11.re,im, a21.re,im } + (extra)
vbroadcast to YMM = { Fx(n+2), Fx(n+2), Fx(n+2), Fx(n+2)}re.im
vmulps { 0.re,im, 0.re,im, a01.re,im, a11.re,im } + (extra)
vbroadcast to YMM = { Fx(n+3), Fx(n+3), Fx(n+3), Fx(n+3)}re.im
vmulps { 0.re,im, 0.re,im, 0.re,im, a01.re,im } + (extra)
vload to YMM = { Fx(n+3), Fx(n+2), Fx(n+1), Fx(n+0)}re.im = vstore YMM = {Yn+0, Yn+1, Yn+2, Yn+3}re.im
IppStatus ippsIIRInitAlloc_32fc( IppsIIRState_32fc** ppState, const Ipp32fc* pTaps, int order, const Ipp32fc* pDlyLine);
タップの次数 = B0,B1,...,Border,A0,A1,...,Aorder
//この関数はメモリーを割り当てて任意の IIR フィルターの状態を初期化する
タップのノルム化: a1=A1/A0 , a2=A2/A0 , ..., border=Border/A0
タップは (6) – (9) に従って再計算され pState 構造の適切なアライメント (32 バイト境界) で、図 1 と図 4 の次数に従って 8 つの係数で格納される
IppStatus ippsIIR_32fc( const Ipp32fc *pSrc, Ipp32fc *pDst, int len,
IppsIIRState_32fc *pState )
{
//第 1 ステージ: FIR フィルターと bk 係数 (インテル® AVX で記述したコード) で "by x" をフィルタリング。一時出力は pDst ベクトル (図 2 および B 係数のアセンブラー関数)
//第 2 ステージ: 4 つのバンドル (インテル® AVX で記述したコード) と再計算した ak 係数で "by y" をフィルタリング (図 5 および A 係数のアセンブラー関数)
}
まとめ
これほど大きな次数の IIR フィルターが信号処理で実際に使用されることはありません。32 未満の次数では、インテル® SSE を使用して IIR フィルターの実装を行っても、共通スキームで蓄積される命令のレイテンシーとフィードバックの依存性により、ベクトル化されていないバージョンではパフォーマンスが向上しませんでした。
ここで説明した (フィードバックの依存性を排除した) インテル® AVX 命令を使用した実装では、次数 6 以上のフィルターで SSE バージョンの 1.6 倍のスピードアップを達成しました (この値はソフトウェア・シミュレーターで計測されたものであり、実際の値は異なる可能性があることに注意してください)。インテル® AVX で最適化されたフィルターの実装は、IPP ライブラリーの将来のバージョンに追加される予定です。
付録 A: 関数コード
- 初期化関数コードのダウンロード: http://software.intel.com/file/1066
- フィルタリング関数コードのダウンロード: http://software.intel.com/file/1057
- B 係数のアセンブラー関数のダウンロード: http://software.intel.com/file/1038
- A 係数のアセンブラー関数のダウンロード: http://software.intel.com/file/1036
参考文献
著者紹介
インテル® ソフトウェア製品のパフォーマンス/最適化に関する詳細は、最適化に関する注意事項 (英語) を参照してください。
編集部追加
最新のインテル® IPP 7.0 では、以下の記事(英語)にリストされている多数の関数についてインテル® AVX による最適化が適用済みです。
http://software.intel.com/en-us/articles/intel-ipp-functions-optimized-for-intel-avx-intel-advanced-vector-extensions/
第2世代インテル® Core™ プロセッサー・ファミリーの性能を活かしきれていないとお考えの方は、是非ともインテル® IPP 並びにインテル® C++ Composer XE をお試しください。評価版のダウンロード、お問い合わせはエクセルソフト株式会社まで。


