この記事は、インテル® ソフトウェア・サイトに掲載されている「PAOS – Packed Array Of Structures」(http://software.intel.com/en-us/articles/paos-packed-array-of-structures/) の日本語参考訳です。
- はじめに
- AOS 形式、FORTRAN (C++ の struct)
- 単純なループ – AOS を使用したオイラー法
- SOA 形式
- PAOS 形式
- 単純なループ – PAOS を使用したオイラー法
- 一般的な問題
- C++ の等価コード
- PAOS で変更するコードセクション
- アセンブリー・コードにおける PAOS の利点
- プログラム変換手法
- AOS に対する PAOS の利点
- ベンチマーク・プログラム
- まとめ
はじめに
多くのプログラマーは、SIMD (Single Instruction Multiple Data) と呼ばれる近年のプロセッサーの小さなベクトル演算機能についてはよくご存知でしょう。インテル® アーキテクチャー (IA-32、IA-64、インテル® 64) では、MMX® 以降、SSE、SSSE、SSE2、SSE3、AVX、AVX2 などで SIMD をサポートしています。SIMD の利点は、データの複数の部分で同じ単一命令を同時に実行できることです。SIMD 命令はさまざまなデータのサイズと型 (byte、word、dword、qword、(dqword)、float、double…) をサポートしますが、この記事では Fortran で REAL*8 (DOUBLE PRECISION) を操作する SIMD を使用します。
多くのプロセッサーは SSE2 または SSE3 をサポートしており、最近のインテル® Core™ i7 プロセッサー (開発コード名: Sandy Bridge) では AVX をサポートしています。また、現在開発段階のインテル® プロセッサー (開発コード名: Haswell) は AVX2 をサポートする予定です。プログラマーから見ると、主な違いは SIMD 命令で操作されるデータの幅 (複数データの数のことで、ベクトル長ともいいます) です。高水準言語のプログラマーは、各命令用の最適なコードパスの生成をコンパイラーに任せていると思いますが、SIMD の MD (Multiple Data – 複数のデータ) の幅について知っておくと、データをレイアウトするときに役立ちます。
サポートされている SIMD の幅は次のとおりです。
SSEn 2 要素幅 double (2 x 64 ビット)
AVX 4 要素幅 double (4 x 64 ビット)
AVX2 4 要素幅 double (4 x 64 ビット)
MIC 8 要素幅 double (8 x 64 ビット) (インテル® Xeon Phi™)
プロセッサーの SIMD 機能を活用するには、プログラマーがアプリケーションで使用するデータレイアウトを適切に設計する必要があります。同じ操作で処理するデータがメモリーで隣接しているレイアウトが理想的です。データ配列を使用する場合、プログラマーは多次元配列の配列インデックスの入れ子レベル以外はプログラミングについて心配する必要はありません。この記事では、単一要素の配列以外のデータに関係するプログラミング問題を取り上げます。
これまで、多くの技術文献では、データレイアウトの手法として、次の 2 つのプログラミング手法が議論されてきました。
AOS 構造体配列 (Array of Structure)
SOA 配列構造体 (Structure of Array)
この記事では、AOS と SOA のハイブリッドである、3 番目の手法を紹介します。
PAOS パックド構造体配列 (Packed Array of Structure)
このプログラミング手法は、次のように呼ぶこともできます。
PSOA 分割配列構造体 (Partitioned Structure of Array)
プログラマーは、開発中に構造体配列 (AOS) を好む傾向があります。これは、デバッグの容易性によるものです。AOS では、構造体への単一ポインターまたは参照をデバッガーで提供することにより、プログラマーは構造体のコンテンツ全体を調査できます。これにより、デバッグ中にプログラムのフローを簡単にたどれるので便利です。
デバッグがほぼ完了すると、プログラマーは配列構造体 (SOA) のパフォーマンスが優れているかどうかを評価できます。動作するコードを変更することになるため、AOS から SOA への変換を行うべきかどうか判断することは難しいでしょう。AOS は、構造体内の操作に際してキャッシュの局所性が優れています。SOA は、構造体間の操作におけるキャッシュの局所性が優れています。データを操作するアプリケーションの大部分は AOS でも SOA でもなく、変換によるパフォーマンスへの影響を予測することは困難です。
この記事では FORTRAN のサンプルコードを使用していることに注意してください。C++ のテンプレートを使用して C++ プログラムを PAOS に適応させるほうが簡単です。
FORTRAN (テンプレートなし) では、より多くの既存コードの変更が必要になります。
この記事で紹介しているサンプルコードは、主に物体に接続されたテザー (紐-ひも) に関する研究で使用されるビードモデル (bead model) 合成プログラムの一部です。このプログラムは、「テザーボール」システムをモデル化するために使用されるもので、ポールに紐で結ばれたバレーボールをイメージすると良いでしょう。
このプログラムは当初、スペースシャトルと長い (20 km の) 導電性テザーで接続された小さな衛星による SED 実験におけるテザー衛星のシミュレーション用に開発されました。シミュレーションでは、導電性テザーが地球磁場を移動すると誘導起電力が発生することが予測されました。最新バージョンのシミュレーション・プログラムは、宇宙 (軌道) エレベーター設計の研究に使用されています。宇宙エレベーターは、赤道上から上空に引き伸ばした約 10 万キロの自立式のテザー (軌道) を伝って電動式の昇降機を上下に移動させ、地上と宇宙間でペイロードを輸送するという構想です。
シミュレーション・プログラムでも使用されるテザーは、物体 (スペースシャトル、衛星、地球、その他) に相互に接続される一連の 1 次元のセグメントです。テザーは一連のばねとして見なすことができます。隣接するセグメントの接続点はビード (bead) と呼ばれます。ビードには、属性の位置、速度、質量、その他の変数 (大部分はフォースベクトル: 重力、外力、弾力、その他) が含まれます。セグメントには、変形前の長さ、変形後の長さ、長さの割合、長さの加速度、弾性部径、空気力学的径、抵抗率、ばね定数、ばね減衰定数、温度、その他の属性が含まれます。ボディーには多くの属性が含まれ、さまざまな物体 (テザー、ブーム、スラスター、その他) が接続されています。惑星、衛星 (月、小惑星、彗星) および宇宙船の初期情報の取得には、JPL (ジェット推進研究所) の天体暦データベースを使用しています。シミュレーターは FORTRAN で記述された包括的なモデリングシステムで、25 年以上にわたって開発されてきたものです。
AOS 形式、FORTRAN (C++ の struct)
type TypeFiniteSolution
SEQUENCE
! REAL(8) variables
! INTEGRATION INTERVAL & LAPSED TIME OF FINITE TETHER SOLN
real :: rDELTIS ! Integration step size
real :: rTISTIM ! Integration time
…
! NOMINAL INSTANTANEOUS DEPLOYED (UNDEFORMED) TETHER LENGTH
real :: rEL
! rate of deployment +out, -in through the X end
real :: rELD
! rate of rate of deployment +out, -in through the X end
real :: rELDD
…
! POSITION VECTOR BETWEEN ATT PTS (INER FRAME)
real :: rELI(3)
! DERIVATIVE OF POS VECTOR BETWEEN ATT PTS (INER FRAME)
real :: rELDI(3)
! 2ND DERIV OF POS VECTOR BETWEEN ATT PTS (INER FRAME)
real :: rELDDI(3)
…
! Position with respect to IP IF
real, pointer :: rBeadIPIF(:,:) ! (3,NumberOfBeads+2)
! Velocity with respect to IP IF
real, pointer :: rBeadDIPIF(:,:) ! (3,NumberOfBeads+2)
! Acceleration with respect to IP IF
real, pointer :: rBeadDDIPIF(:,:) ! (3,NumberOfBeads+2)
…
! SEGMENT LENGTH AND LENGTH RATE
real, pointer :: rELBSG(:) ! (NumberOfBeads+1)
real, pointer :: rELBSGD(:) ! (NumberOfBeads+1)
…
end type TypeFiniteSolution
次のメモリーレイアウトを見てください。
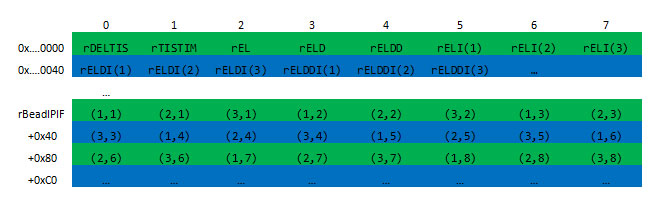
緑のバーは 64 バイト (8 double) の 1 つのキャッシュラインを表し、青のバーは隣接するキャッシュラインを表しています。最近のプロセッサーの多くは、2 つの隣接するキャッシュラインを同時にフェッチします。SSE を活用するようにレイアウトを再構成すると、メモリーレイアウトは次のようになりました。
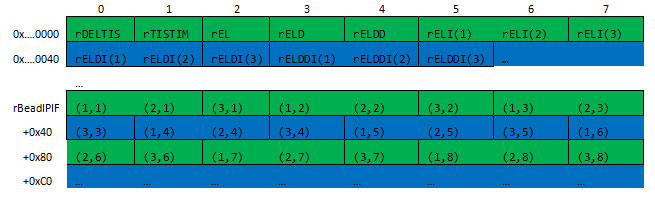
最後の積分展開ステップのみ

図中のセルは最適化の可能性を表しています。2 つの隣接する類似したセルがボックスでグループ化された場合に限り、SSE ベクトル化の可能性があります。ビード位置の大きな配列 (rBeadIPIF) は、2 つの構成で示されています。最初のボックスグループは、ビードおよびビード間計算コードの主な部分を表しています。2 番目のボックスグループは、(dV * dT) で位置を進めることができる最後のループ最適化のみを表しています。
上記の図は、AOS 形式のベクトル化の可能性を示しています。
スカラーのベクトル化の可能性はない。
小さな次元のベクトル (3) (3,3) は半分のベクトル化の可能性がある。
大きなベクトル (3,nBeads) の主な部分は半分のベクトル化の可能性がある。
大きなベクトル (3,nBeads) の最後の積分は完全なベクトル化の可能性がある。
上記は仮定にすぎないため、コードサンプルを実際に調べることにしましょう。
単純なループ – AOS を使用したオイラー法
ビードの速度と積分ステップ区間に基づいてビードの位置を進める、積分プロセスの最終段階を調べます。このプロセスはオイラー法として知られています。
次のコードは、AOS に対する PAOS の最適化の可能性が最も少ない部分の 1 つであることに注意してください。
type TypeFiniteSolution
call EULINTxyz(DELTIS, NBEAD, rBeadDIPIF(1:3,1:NBEAD), rBeadIPIF(1:3,1:NBEAD))
...
subroutine EULINTxyz_r_n_r_r(dT, n, dX, X)
implicit none
real :: dT
integer :: n
real :: dX(1:3,1:n)
real :: X(1:3,1:n)
integer :: i,j
do i=1,n
do j=1,3
X(j,i) = X(j,i) + dX(j,i) * dT
end do
end do
end subroutine EULINTxyz_r_n_r_r
(上記のコードはジェネリック・インターフェイス署名 “_r_n_r_r” を含んでいます)
オイラー法の AOS アセンブリー・コード
; parameter 1(DT): rcx
; parameter 2(N): rdx
; parameter 3(DX): r8
; parameter 4(X): r9
;;; recursive subroutine EULINTxyz_r_n_r_r(dT, n, dX, X)
push rbp ; save stack frame pointer
sub rsp, 48 ; allocate stack space
lea rbp, QWORD PTR [32+rsp] ; set new stack frame pointer
movsxd rax, DWORD PTR [rdx] ; rax = n
mov QWORD PTR [rbp], rax ; temp0 = n (unnecessary)
mov QWORD PTR [8+rbp], rax ; temp1 = n (unnecessary)
;;; implicit none
;;; real :: dT
;;; integer :: n
;;; real :: dX(1:3,1:n)
;;; real :: X(1:3,1:n)
;;; integer :: i,j
;;;
;;; do i=1,n
movsxd r10, DWORD PTR [rdx] ; r10 = n (could have obtained from rax)
xor edx, edx ; zero iteration count
xor eax, eax ; zero linear index into both arrays
test r10, r10 ; if(n <= 0)
jle .B5.5 ; Prob 3% ; goto .B5.5
.B5.2::
;;; do j=1,3
;;; X(j,i) = X(j,i) + dX(j,i) * dT
vmovsd xmm0, QWORD PTR [rcx] ; xmm0= dT (scalar)
ALIGN 16 ; align following code to 16 byte address
.B5.3:: : loop:
vmulsd xmm1, xmm0, QWORD PTR [rax+r8] ; xmm1 = dT * dX(index) (scalar)
inc rdx ; ++iteration count
vmulsd xmm3, xmm0, QWORD PTR [8+rax+r8] ; xmm3 = dT * dX(index+1) (scalar)
vmulsd xmm5, xmm0, QWORD PTR [16+rax+r8] ; xmm5 = dT * dX(index+2) (scalar)
vaddsd xmm2, xmm1, QWORD PTR [rax+r9] ; xmm2 = dT * dX(index) + X(index) (scalar)
vaddsd xmm4, xmm3, QWORD PTR [8+rax+r9] ; xmm4 = dT * dX(index+1) + X(index+1) (scalar)
vaddsd xmm1, xmm5, QWORD PTR [16+rax+r9] ; xmm1 = dT * dX(index+2) + X(index+2) (scalar)
vmovsd QWORD PTR [rax+r9], xmm2 ; X(index) = dT * dX(index) + X(index) (scalar)
vmovsd QWORD PTR [8+rax+r9], xmm4 ; X(index+1) = dT * dX(index+1) + X(index+1) (s)
vmovsd QWORD PTR [16+rax+r9], xmm1 ; X(index+2) = dT * dX(index+2) + X(index+2) (s)
add rax, 24 ; index += 3
cmp rdx, r10 ; if(iteration count < n)
jb .B5.3 ; Prob 82% ; goto loop
.B5.5::
;;; end do
;;; end do
;;; end subroutine EULINTxyz_r_n_r_r
lea rsp, QWORD PTR [16+rbp] ; restore stack pointer
pop rbp ; restore stack frame
ret
コンパイラーにより生成されたコードに関する最適化サポート:
ループがアラインされました (OK)
内部ループと外部ループが融合されました (OK)
スタックに 2 つの不要な n が保存されました (NG)
計算はすべてスカラーです (最適ではない)
プログラマーは、TRANSFER を使用して (3,NBEAD) 2 次元配列を (3*NBEAD) 1 次元配列にレイアウトし直してこれらの問題に対処することもできます。ただし、テザーのビード (およびセグメント) 情報を処理するループをすべて書き直す必要があるため、プログラム内の非常に多くのループを変更することになります。この記事の目的は、コンパイラーに多くの作業をしてもらえるようなコードに変更することです。
SOA 形式
! REAL variables (set compiler option for default real == real(8)
! INTEGRATION INTERVAL & LAPSED TIME OF FINITE TETHER SOLN
real, pointer :: rDELTIS(:) ! (NumberOfTethers)
real, pointer :: rTISTIM(:) ! (NumberOfTethers)
…
! NOMINAL INSTANTANEOUS DEPLOYED (UNDEFORMED) TETHER LENGTH
real, pointer :: rEL(:) ! (NumberOfTethers)
! rate of deployment +out, -in through the X end
real, pointer :: rELD(:) ! (NumberOfTethers)
! rate of rate of deployment +out, -in through the X end
real, pointer :: rELDD(:) ! (NumberOfTethers)
…
! POSITION VECTOR BETWEEN ATT PTS (INER FRAME)
real, pointer :: rELI(:,:) ! (3, NumberOfTethers)
! DERIVATIVE OF POS VECTOR BETWEEN ATT PTS (INER FRAME)
real, pointer :: rELDI(:,:) ! (3, NumberOfTethers)
! 2ND DERIV OF POS VECTOR BETWEEN ATT PTS (INER FRAME)
real, pointer :: rELDDI(:,:) ! (3, NumberOfTethers)
…
! Position with respect to IP IF
! *** note change in index order and number of indexes
real, pointer :: rBeadIPIF(:,:,:) ! (NumberOfBeads+2, 3, NumberOfTethers)
! Velocity with respect to IP IF
real, pointer :: rBeadDIPIF(:,:,:) ! (NumberOfBeads+2, 3, NumberOfTethers)
! Acceleration with respect to IP IF
real, pointer :: rBeadDDIPIF(:,:,:) ! (NumberOfBeads+2, 3, NumberOfTethers)
…
! SEGMENT LENGTH AND LENGTH RATE
real, pointer :: rELBSG(:,:) ! (NumberOfBeads+1, NumberOfTethers)
real, pointer :: rELBSGD(:,:) ! (NumberOfBeads+1, NumberOfTethers)
…
または:
real, pointer :: rBeadIPIF(:,:,:) ! (NumberOfTethers, NumberOfBeads+2, 3)
または:
real, pointer :: rBeadIPIF(:,:,:) ! (NumberOfTethers, 3, NumberOfBeads+2)
または:
real, pointer :: rBeadIPIF(:,:,:) ! (3, NumberOfTethers, NumberOfBeads+2)
SOA のインデックス順は重要で、プログラミング要件に応じて変わります。このアプリケーションで特に注意すべき点は、ビード間計算とビード/ビード内計算のパフォーマンスへの影響です。SOA は両方ではなく 1 つの型の計算に適しています。
SOA のデバッグには、個々の配列要素の検査と配列インデックスの同期が必要になります。この処理は AOS 形式よりも困難です。「ポインター」と「割り当て可能」を選択したことは、個人的なプログラミングの好みであることをお知らせしておきます。
この記事で示されたようなアプリケーションでは、プログラマーはスカラーおよび小さなベクトルを AOS 形式で処理し、NumberOfBead サイズの割り当てが大きなベクトルにのみ SOA 変換を行うことになるでしょう。プログラマーがインデックス順の影響を判断するのは困難です。また、異なるインデックス順で複数の変換を行うには、順序を変更して、それぞれパフォーマンス・テストを実行しなければなりません。アプリケーションの SOA 変換は、計算の一部にのみ部分的に実装されます。
PAOS 形式
パックド構造体配列 (PAOS) には、いくつかの表現があります。ここでは、1 つの SSE 表現 (2 要素幅 double) と 2 つの AVX/AVX2 表現 (4 要素幅 double および 3 要素幅 double) の 3 つの表現を使用します。
! AVX four-wide double vector
type TypeYMM
SEQUENCE
real(8) :: v(0:3)
end type TypeYMM
! AVX three-wide double vector
type TypeYMM02
SEQUENCE
real(8) :: v(0:2)
end type TypeYMM02
! SSE two-wide double vector
type TypeXMM
SEQUENCE
real(8) :: v(0:1)
end type TypeXMM
type TypeFiniteSolution
SEQUENCE
! REAL variables (4-wide AVX)
! INTEGRATION INTERVAL & LAPSED TIME OF FINITE TETHER SOLN
type(TypeYMM) :: rDELTIS ! Integration step size
type(TypeYMM) :: rTISTIM ! Integration time
…
! NOMINAL INSTANTANEOUS DEPLOYED (UNDEFORMED) TETHER LENGTH
type(TypeYMM) :: rEL
! rate of deployment +out, -in through the X end
type(TypeYMM) :: rELD
! rate of rate of deployment +out, -in through the X end
type(TypeYMM) :: rELDD
…
! POSITION VECTOR BETWEEN ATT PTS (INER FRAME)
type(TypeYMM) :: rELI(3)
! DERIVATIVE OF POS VECTOR BETWEEN ATT PTS (INER FRAME)
type(TypeYMM) :: rELDI(3)
! 2ND DERIV OF POS VECTOR BETWEEN ATT PTS (INER FRAME)
type(TypeYMM) :: rELDDI(3)
…
! Position with respect to IP IF
type(TypeYMM), pointer :: rBeadIPIF(:,:) ! (3,NumberOfBeads+2)
! Velocity with respect to IP IF
type(TypeYMM), pointer :: rBeadDIPIF(:,:) ! (3,NumberOfBeads+2)
! Acceleration with respect to IP IF
type(TypeYMM), pointer :: rBeadDDIPIF(:,:) ! (3,NumberOfBeads+2)
…
! SEGMENT LENGTH AND LENGTH RATE
type(TypeYMM), pointer :: rELBSG(:) ! (NumberOfBeads+1)
type(TypeYMM), pointer :: rELBSGD(:) ! (NumberOfBeads+1)
…
end type TypeFiniteSolution
PAOS のデータ構成は、変数型「real」を「type(TypeYMM)」に変更する点を除いて AOS と同じです。配列のインデックス・スキームは同じままです。PAOS のデバッグも、AOS とほぼ同様に行うことができます。4 要素幅変数を調べるには、SIMD ベクトルを分解しなければなりません。
インメモリー 4 要素幅 YMM のレイアウトは次のとおりです。

インメモリー 2 要素幅 XMM のレイアウトは次のとおりです。
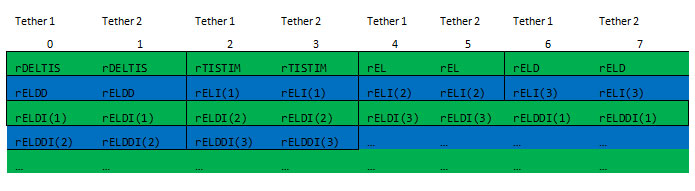
すべてのテザーを集約する際、すべての参照に完全な SIMD ベクトル化が利用可能であることに注意してください。個々のアクセスを行うコードの部分はキャッシュラインを別途ロードする影響を受けますが、計算の主な部分はテザーの集約に対して行われます。
単純なループ – PAOS を使用したオイラー法
call EULINTxyz(DELTIS, NBEAD, rBeadDDIPIF(1:3,1:NBEAD), rBeadDIPIF(1:3,1:NBEAD))
...
subroutine EULINTxyz_ymm_n_ymm_ymm(dT, n, dX, X)
USE MOD_ALL
implicit none
type(TypeYMM) :: dT
integer :: n
type(TypeYMM) :: dX(1:3,1:n)
type(TypeYMM) :: X(1:3,1:n)
integer :: i,j
do i=1,n
do j=1,3
!DEC$ VECTOR ALWAYS
X(j,i).v = X(j,i).v + dX(j,i).v * dT.v
end do
end do
end subroutine EULINTxyz_ymm_n_ymm_ymm
(ジェネリック・インターフェイスが署名サフィックス “_ymm_n_ymm_ymm” を選択していることに注意してください。)
PAOS アセンブリー・コード
; parameter 1(DT): rcx
; parameter 2(N): rdx
; parameter 3(DX): r8
; parameter 4(X): r9
;;; recursive subroutine EULINTxyz_ymm_n_ymm_ymm(dT, n, dX, X)
push rbp ; save stack frame pointer
sub rsp, 48 ; allocate stack space
lea rbp, QWORD PTR [32+rsp] ; set new stack frame pointer
movsxd rax, DWORD PTR [rdx] ; rax = n
mov QWORD PTR [rbp], rax ; temp0 = n (unnecessary)
mov QWORD PTR [8+rbp], rax ; temp1 = n (unnecessary)
;;; type(TypeYMM) :: dT
;;; integer :: n
;;; type(TypeYMM) :: dX(1:3,1:n)
;;; type(TypeYMM) :: X(1:3,1:n)
;;; integer :: i,j
;;;
;;; do i=1,n
movsxd r10, DWORD PTR [rdx] ; r10 = n (could have obtained from rax)
xor edx, edx ; zero loop iteration count
xor eax, eax ; zero linear index into dX and X
test r10, r10 ; if(n <= 0)
jle .B6.5 ; Prob 3% ; goto .B6.6
.B6.2::
;;; do j=1,3
;;; !DEC$ VECTOR ALWAYS
;;; X(j,i).v = X(j,i).v + dX(j,i).v * dT.v
vmovupd xmm1, XMMWORD PTR [rcx] ; xmm1 = dT.v(0:1)
vmovupd xmm0, XMMWORD PTR [16+rcx] ; xmm0 = dT.v(2:3)
.B6.3:: ; loop:
vmulpd xmm2, xmm1, XMMWORD PTR [rax+r8] ; xmm2=dT(index).v(0:1) * dX(index).v(0:1)
vmulpd xmm4, xmm0, XMMWORD PTR [16+rax+r8] ; xmm4=dT(index).v(2:3) * dX(index).v(2:3)
vaddpd xmm3, xmm2, XMMWORD PTR [rax+r9] ; xmm3=dT(index).v(0:1)*dX(index).v(0:1)+X(index).v(0:1)
vaddpd xmm5, xmm4, XMMWORD PTR [16+rax+r9] ; xmm5=dT(index).v(2:3)*dX(index).v(2:3)+X(index).v(2:3)
vmulpd xmm2, xmm1, XMMWORD PTR [32+rax+r8] ; xmm2 = dT.v(0:1) * dX(index+1).v(0:1)
; X(index).v(0:1)= dT(index).v(0:1) * dX(index).v(0:1) + X(index).v(0:1)
vmovupd XMMWORD PTR [rax+r9], xmm3
; X(index).v(2:3)= dT(index).v(2:3) * dX(index).v(2:3) + X(index).v(2:3)
vmovupd XMMWORD PTR [16+rax+r9], xmm5
vmulpd xmm4, xmm0, XMMWORD PTR [48+rax+r8] ; xmm4 = dT.v(2:3) * dX(index+1).v(2:3)
; xmm3 = dT.v(0:1) * dX(index+1).v(0:1) + X(index+1).v(0:1)
vaddpd xmm3, xmm2, XMMWORD PTR [32+rax+r9]
; xmm5 = dT.v(2:3) * dX(index+1).v(2:3) + X(index+1).v(2:3)
vaddpd xmm5, xmm4, XMMWORD PTR [48+rax+r9]
vmulpd xmm2, xmm1, XMMWORD PTR [64+rax+r8] ; xmm2 = dT(index+2).v(0:1) * dX(index+2).v(0:1)
; X(index+1).v(0:1)= dT(index+1).v(0:1) * dX(index+1).v(0:1) + X(index+1).v(0:1)
vmovupd XMMWORD PTR [32+rax+r9], xmm3
; X(index+1).v(2:3)= dT(index+1).v(2:3) * dX(index+1).v(2:3) + X(index+1).v(2:3)
vmovupd XMMWORD PTR [48+rax+r9], xmm5
vmulpd xmm4, xmm0, XMMWORD PTR [80+rax+r8] ; xmm4 = dT(index+2).v(2:3) * dX(index+2).v(2:3)
;xmm3=dT(index+2).v(0:1)*dX(index+2).v(0:1)+X(index+2).v(0:1)
vaddpd xmm3, xmm2, XMMWORD PTR [64+rax+r9]
; xmm5 = dT(index+2).v(2:3) * dX(index+2).v(2:3) + X(index+2).v(2:3)
vaddpd xmm5, xmm4, XMMWORD PTR [80+rax+r9]
; X(index+2).v(0:1)= dT(index+2).v(0:1) * dX(index+2).v(0:1) + X(index+2).v(0:1)
vmovupd XMMWORD PTR [64+rax+r9], xmm3
; X(index+2).v(2:3)= dT(index+2).v(2:3) * dX(index+2).v(2:3) + X(index+2).v(2:3)
vmovupd XMMWORD PTR [80+rax+r9], xmm5
inc rdx ; ++loop count
add rax, 96 ; index += 3
cmp rdx, r10 ; if(loop count < n)
jb .B6.3 ; Prob 82% ; goto loop
.B6.5::
;;; end do
;;; end do
;;; end subroutine EULINTxyz_ymm_n_ymm_ymm
アセンブリー・コードを調べると、xmm レジスターとともに先頭の文字が v で始まる命令 (vaddpd など) が使用されていることが分かります。これらの命令は、2 要素幅のパックドダブルを表します。AVX は 4 要素幅のパックドダブルをサポートしますが、Sandy Bridge アーキテクチャーは 2 要素幅のフェッチとストアを実行します。4 要素幅のフェッチやストアを行うこともできますが、この場合、隣接するフェッチとストアを同時に行うことになります。万一これらの 2 要素幅のフェッチやストアのデータが同じキャッシュラインに及ぶと、パイプラインはストールします。2 要素幅のフェッチとストアを使用することにより、コード最適化でフェッチやストアと同時に計算を行う命令を交互に配置することができます。
vmulpd xmm2, xmm1, XMMWORD PTR [rax+r8] ; xmm2=dT(index).v(0:1) * dX(index).v(0:1) vmulpd xmm4, xmm0, XMMWORD PTR [16+rax+r8] ; xmm4=dT(index).v(2:3) * dX(index).v(2:3) vaddpd xmm3, xmm2, XMMWORD PTR [rax+r9] ; xmm3=dT(index).v(0:1)*dX(index).v(0:1)+X(index).v(0:1) vaddpd xmm5, xmm4, XMMWORD PTR [16+rax+r9] ; xmm5=dT(index).v(2:3)*dX(index).v(2:3)+X(index).v(2:3) ------------ または ------------- vmulpd ymm2, ymm1, XMMWORD PTR [rax+r8] ; ymm2=dT(index).v(0:3) * dX(index).v(0:3) vaddpd ymm3, ymm2, XMMWORD PTR [rax+r9] ; ymm3=dT(index).v(0:3)*dX(index).v(0:3)+X(index).v(0:3)
Sandy Bridge アーキテクチャーでは、例えば、.v(0:1) と .v(2:3) は異なるキャッシュラインに存在するために、フェッチがキャッシュラインで分割される場合を除いて、2 つはほぼ同時に実行されます。キャッシュラインが分割された状況では、2 要素幅命令はより高速に実行されます。
Ivy Bridge アーキテクチャーでは、4 要素幅のフェッチとストア操作を 4 要素幅の計算と一緒に実行できるため、この制限はなくなります。
コードの多くの場所で、コンパイラーは 4 要素幅のフェッチとストアを実行します (後の例を参照)。
一般的な問題
先に調べたオイラー展開コードは、AOS に対する PAOS の最も望ましくない例であり、ループの処理も変則的でした。一般的なループを調べることにしましょう。次のループは、ばねの張力を計算します。
ループの AOS バージョン
!***********************************************************
! FORM SEGMENT VECTOR BETWEEN ADJACENT BEADS (IN INER FRAME)
!***********************************************************
do i=1,3
! Determine TUI at 1/2 integration step from now
! using current velocity and acceleration
! Position of X-End of segment
TOSVX1(i) = rBeadIPIF(i,JSEG-1) &
& + (rBeadDIPIF(i,JSEG-1) * (rDELTIS/2.0_8)) &
& + (rBeadDDIPIF(i,JSEG-1) * (rDELTIS**2/4.0_8))
! Position of Y-End of segment
TOSVX2(i) = rBeadIPIF(i,JSEG).v &
& + (rBeadDIPIF(i,JSEG) * (rDELTIS/2.0_8)) &
& + (rBeadDDIPIF(i,JSEG) * (rDELTIS**2/4.0_8))
! SUI X->Y
SUI(i) = TOSVX2(i) - TOSVX1(i)
end do
! CALC DIST BETWEEN BEADS ADJACENT TO THIS SEGMENT
!-------------------------------------------------
DUMEL = dsqrt(SUI(1)**2 + SUI(2)**2 + SUI(3)**2)
rELBSG(JSEG) = DUMEL
! TALLY TOTAL SPATIAL ARC LENGTH
ARCTOTlocal = ARCTOTlocal + DUMEL
!---------------------------------------------
! POPULATE THE JSEG ELEMENT OF THE BBTUI ARRAY
!---------------------------------------------
! FORM UNIT VECTOR FROM X-END TO Y-END OF BEAD SEGMENT
if(DUMEL .ne. 0.0_8) then
TUI = SUI / DUMEL
else
call RandomUnitVector(TUI)
endif
rBBTUI(1:3,JSEG) = TUI(1:3)
! recompute velocity of Bead 0
if(JSEG .eq. 1) then
rBeadDIPIF(:,0) = rAVI + (TUI * rELD)
endif
! ARC LENGTH WR/T UNDEFORMED TETHER
!--------------------------------------------
! (NOTE, NEGATIVE SIGN REFLECTS MU DEFINITION FROM FAR END)
rDSDU(JSEG) = - DUMEL/ELBis
!**************************************************************
! FORM DERIVATIVE OF SEGMENT VECTOR (INER FRAME)
!**************************************************************
! compute equivelent to
! SUDI = BUDI(JB1:JB1+2) - BUDI(JB1-3:JB1-1) + ELSGX_x_UITDI_ELSGXD_x_UITI
SUDI = rBeadDIPIF(:,JSEG) - rBeadDIPIF(:,JSEG-1)
! CALC DERIV OF DIST BETWEEN BEADS ADJACENT TO SEGMENT
!-----------------------------------------------------
DUMELD = DOT(TUI,SUDI)
rELBSGD(JSEG) = DUMELD
!--------------------------------------------------------
! POPULATE THE SEGMENT DATA ARRAY'S FOR THIS JSEG ELEMENT
! (FOR AVERAGING AND NUMERICAL DIFF IN DEPLOY FLOW CALCS)
!--------------------------------------------------------
! BBTUDI(1:3,JSEG) = (SUDI / DUMEL) + (SUI * -DUMELD/DUMEL**2)
if(DUMEL .ne. 0.0_8) then
rBBTUDI(1:3,JSEG) =((SUDI) + (SUI * -DUMELD/DUMEL)) / DUMEL
else
rBBTUDI(1:3,JSEG) = 0.0_8
endif
! FINALLY, ARC LENGTH DERIV WR/T UNDEFORMED TETHER, AND ITS TIME DERIV
!---------------------------------------------------------------------
! (NOTE, NEGATIVE SIGN REFLECTS MU DEFINITION FROM FAR END)
rDSDUD(JSEG) = - ( DUMELD - DUMEL*ELDoverEL )/ELBis
end do
(コードが読みやすいようにポインターが削除されていることに注意してください)
ループの PAOS バージョン
DO JSEG = 1,JSEGlast
!***********************************************************
! FORM SEGMENT VECTOR BETWEEN ADJACENT BEADS (IN INER FRAME)
!***********************************************************
do i=1,3
! Determine TUI at 1/2 integration step from now
! using current velocity and acceleration
! Position of X-End of segment
TOSVX1(i).v = rBeadIPIF(i,JSEG-1).v &
& + (rBeadDIPIF(i,JSEG-1).v * (rDELTIS.v/2.0_8)) &
& + (rBeadDDIPIF(i,JSEG-1).v * (rDELTIS.v**2/4.0_8))
! Position of Y-End of segment
TOSVX2(i).v = rBeadIPIF(i,JSEG).v &
& + (rBeadDIPIF(i,JSEG).v * (rDELTIS.v/2.0_8)) &
& + (rBeadDDIPIF(i,JSEG).v * (rDELTIS.v**2/4.0_8))
! SUI X->Y
SUI(i).v = TOSVX2(i).v - TOSVX1(i).v
end do
! CALC DIST BETWEEN BEADS ADJACENT TO THIS SEGMENT
!-------------------------------------------------
DUMEL.v = dsqrt(SUI(1).v**2 + SUI(2).v**2 + SUI(3).v**2)
rELBSG(JSEG) = DUMEL
! TALLY TOTAL SPATIAL ARC LENGTH
ARCTOTlocal.v = ARCTOTlocal.v + DUMEL.v
!---------------------------------------------
! POPULATE THE JSEG ELEMENT OF THE BBTUI ARRAY
!---------------------------------------------
! FORM UNIT VECTOR FROM X-END TO Y-END OF BEAD SEGMENT
! *** code change for SIMD horizontal operation ***
do s=0,sLast
if(DUMEL.v(s) .ne. 0.0_8) then
TUI.v(s) = SUI.v(s) / DUMEL.v(s)
else
call RandomUnitVector(TUI.v(s))
endif
end do
rBBTUI(1:3,JSEG) = TUI(1:3)
! recompute velocity of Bead 0
if(JSEG .eq. 1) then
do i=1,3
rBeadDIPIF(i,0).v = rAVI(i).v + (TUI(i).v * rELD.v)
end do
endif
! ARC LENGTH WR/T UNDEFORMED TETHER
!--------------------------------------------
! (NOTE, NEGATIVE SIGN REFLECTS MU DEFINITION FROM FAR END)
rDSDU(JSEG).v = - DUMEL.v/ELBis.v
!**************************************************************
! FORM DERIVATIVE OF SEGMENT VECTOR (INER FRAME)
!**************************************************************
do i=1,3
SUDI(i).v = rBeadDIPIF(i,JSEG).v - rBeadDIPIF(i,JSEG-1).v
end do
! CALC DERIV OF DIST BETWEEN BEADS ADJACENT TO SEGMENT
!-----------------------------------------------------
DUMELD = DOT(TUI,SUDI)
rELBSGD(JSEG) = DUMELD
!--------------------------------------------------------
! POPULATE THE SEGMENT DATA ARRAY'S FOR THIS JSEG ELEMENT
! (FOR AVERAGING AND NUMERICAL DIFF IN DEPLOY FLOW CALCS)
!--------------------------------------------------------
if((DUMEL.v(0) .ne. 0.0_8) .and. (DUMEL.v(1) .ne. 0.0_8) &
& .and. (DUMEL.v(2) .ne. 0.0_8) .and. (DUMEL.v(3) .ne. 0.0_8)) then
do i=1,3
rBBTUDI(i,JSEG).v =((SUDI(i).v) + (SUI(i).v * -DUMELD.v / DUMEL.v)) / DUMEL.v
end do
else
do s=0,sLast ! *** code change for SIMD horizontal operation ***
if(DUMEL.v(s) .ne. 0.0_8) then
do i=1,3
rBBTUDI(i,JSEG).v(s) = ((SUDI(i).v(s)) &
& + (SUI(i).v(s) * -DUMELD.v(s) / DUMEL.v(s))) / DUMEL.v(s)
end do
else
do i=1,3
rBBTUDI(i,JSEG).v(s) = 0.0_8
end do
endif
end do ! *** code change for SIMD horizontal operation ***
endif
! FINALLY, ARC LENGTH DERIV WR/T UNDEFORMED TETHER, AND ITS TIME DERIV
!---------------------------------------------------------------------
! (NOTE, NEGATIVE SIGN REFLECTS MU DEFINITION FROM FAR END)
rDSDUD(JSEG).v = - ( DUMELD.v - DUMEL.v * ELDoverEL.v ) / ELBis.v
end do
では、メインループ内の最初の小さなループを分解しましょう。このループは、積分区間の途中に存在する 2 つのポイント (ビード) 間のベクトルを計算します。このベクトルは、(2 つのセグメント最後の各ビードの) 2 つのばねのフォースベクトルの方向を決定するために後で使用されます。
AOS
do i=1,3
! Determine TUI at 1/2 integration step from now
! using current velocity and acceleration
! Position of X-End of segment
TOSVX1(i) = rBeadIPIF(i,JSEG-1) &
& + (rBeadDIPIF(i,JSEG-1)*(rDELTIS/2.0_8)) &
& + (rBeadDDIPIF(i,JSEG-1)*(rDELTIS**2/4.0_8))
! Position of Y-End of segment
TOSVX2(i) = rBeadIPIF(i,JSEG) &
& + (rBeadDIPIF(i,JSEG)*(rDELTIS/2.0_8)) &
& + (rBeadDDIPIF(i,JSEG)*(rDELTIS**2/4.0_8))
! SUI X->Y
SUI(i) = TOSVX2(i) - TOSVX1(i)
end do
PAOS
do i=1,3
! Determine TUI at 1/2 integration step from now
! using current velocity and acceleration
! Position of X-End of segment
TOSVX1(i).v = rBeadIPIF(i,JSEG-1).v &
& + (rBeadDIPIF(i,JSEG-1).v * (rDELTIS.v/2.0_8)) &
& + (rBeadDDIPIF(i,JSEG-1).v * (rDELTIS.v**2/4.0_8))
! Position of Y-End of segment
TOSVX2(i).v = rBeadIPIF(i,JSEG).v &
& + (rBeadDIPIF(i,JSEG).v * (rDELTIS.v/2.0_8)) &
& + (rBeadDDIPIF(i,JSEG).v * (rDELTIS.v**2/4.0_8))
! SUI X->Y
SUI(i).v = TOSVX2(i).v - TOSVX1(i).v
end do
算術演算子を含む文にサフィックス “.v” が追加されていることに注意してください。これらのデータ型用に演算子を多重定義した関数を記述する方法を選択すればサフィックスを追加する必要はありませんが、デバッグ上の理由 (デバッグビルドでコードをインライン展開する) により、ここではサフィックスを追加しています。
3 つの文の小さなループの AOS アセンブラー・コード
mov r12, QWORD PTR [80+rbp] ;178.25
mov r11, QWORD PTR [176+rbp] ;179.18
mov rdi, QWORD PTR [152+rbp] ;179.18
mov r8, QWORD PTR [272+rbp] ;180.18
mov rax, QWORD PTR [56+rbp] ;178.25
mov rdx, QWORD PTR [248+rbp] ;180.18
mov QWORD PTR [896+rbp], r12 ;178.25
mov QWORD PTR [928+rbp], r11 ;179.18
mov QWORD PTR [912+rbp], rdi ;179.18
mov QWORD PTR [936+rbp], r8 ;180.18
mov r9, QWORD PTR [rbp] ;178.13
mov r15, QWORD PTR [64+rbp] ;178.25
mov rcx, QWORD PTR [88+rbp] ;178.25
mov r12, QWORD PTR [184+rbp] ;179.18
mov r11, QWORD PTR [160+rbp] ;179.18
mov r14, QWORD PTR [96+rbp] ;178.25
mov rdi, QWORD PTR [192+rbp] ;179.15
mov r8, QWORD PTR [256+rbp] ;180.18
mov r10, QWORD PTR [280+rbp] ;180.18
mov QWORD PTR [920+rbp], rax ;178.25
mov QWORD PTR [904+rbp], rdx ;180.18
cmp rax, 8 ;180.18
jne .B1.12 ; Prob 50% ;180.18
.B1.9:: ; Preds .B1.8
cmp QWORD PTR [912+rbp], 8 ;180.18
jne .B1.12 ; Prob 50% ;180.18
.B1.10:: ; Preds .B1.9
cmp QWORD PTR [904+rbp], 8 ;180.18
jne .B1.12 ; Prob 50% ;180.18
.B1.11:: ; Preds .B1.10
mov QWORD PTR [960+rbp], rbx ;
mov rbx, QWORD PTR [936+rbp] ;182.13
imul r10, rbx ;182.13
mov QWORD PTR [968+rbp], r10 ;182.13
mov r10, rsi ;182.25
mov rax, QWORD PTR [896+rbp] ;182.13
imul r10, rax ;182.25
imul rcx, rax ;182.13
add r10, r9 ;182.13
shl r15, 3 ;182.13
sub r10, rcx ;182.13
mov QWORD PTR [976+rbp], r15 ;182.13
sub r10, r15 ;182.13
mov r15, rsi ;183.18
mov rdx, QWORD PTR [928+rbp] ;182.13
imul r15, rdx ;183.18
imul r12, rdx ;182.13
add r15, r14 ;182.13
shl r11, 3 ;182.13
sub r15, r12 ;182.13
mov QWORD PTR [984+rbp], r11 ;182.13
sub r15, r11 ;182.13
mov r11, rsi ;184.18
imul r11, rbx ;184.18
vmulsd xmm0, xmm10, QWORD PTR [8+r15] ;183.45
mov QWORD PTR [944+rbp], rsi ;
lea rsi, QWORD PTR [-1+rsi] ;178.25
imul rdx, rsi ;179.18
imul rax, rsi ;178.25
imul rbx, rsi ;180.18
vaddsd xmm0, xmm0, QWORD PTR [8+r10] ;183.15
add r11, rdi ;182.13
add r14, rdx ;178.13
mov QWORD PTR [952+rbp], rdi ;
sub r14, r12 ;178.13
mov rdi, QWORD PTR [968+rbp] ;182.13
sub r11, rdi ;182.13
shl r8, 3 ;182.13
add r9, rax ;178.13
sub r11, r8 ;182.13
sub r9, rcx ;178.13
sub r14, QWORD PTR [984+rbp] ;178.13
mov rcx, QWORD PTR [952+rbp] ;178.13
add rcx, rbx ;178.13
vmulsd xmm5, xmm8, QWORD PTR [8+r11] ;184.49
sub rcx, rdi ;178.13
sub rcx, r8 ;178.13
vaddsd xmm14, xmm0, xmm5 ;182.13
vmulsd xmm0, xmm10, QWORD PTR [8+r14] ;179.47
vmulsd xmm5, xmm8, QWORD PTR [8+rcx] ;180.51
vmulsd xmm1, xmm8, QWORD PTR [24+rcx] ;180.51
sub r9, QWORD PTR [976+rbp] ;178.13
vmovsd QWORD PTR [704+rbp], xmm14 ;182.13
mov QWORD PTR [888+rbp], rsi ;178.25
mov rbx, QWORD PTR [960+rbp] ;186.11
mov rsi, QWORD PTR [944+rbp] ;186.11
vaddsd xmm0, xmm0, QWORD PTR [8+r9] ;179.15
vaddsd xmm13, xmm0, xmm5 ;178.13
vmulsd xmm0, xmm10, QWORD PTR [16+r15] ;183.45
vmulsd xmm5, xmm8, QWORD PTR [16+r11] ;184.49
vaddsd xmm0, xmm0, QWORD PTR [16+r10] ;183.15
vmovsd QWORD PTR [736+rbp], xmm13 ;178.13
vaddsd xmm12, xmm0, xmm5 ;182.13
vmulsd xmm0, xmm10, QWORD PTR [16+r14] ;179.47
vmulsd xmm5, xmm8, QWORD PTR [16+rcx] ;180.51
vaddsd xmm0, xmm0, QWORD PTR [16+r9] ;179.15
vmovsd QWORD PTR [712+rbp], xmm12 ;182.13
vaddsd xmm11, xmm0, xmm5 ;178.13
vmulsd xmm0, xmm10, QWORD PTR [24+r15] ;183.45
vmulsd xmm5, xmm8, QWORD PTR [24+r11] ;184.49
vaddsd xmm0, xmm0, QWORD PTR [24+r10] ;183.15
vmovsd QWORD PTR [744+rbp], xmm11 ;178.13
vaddsd xmm5, xmm0, xmm5 ;182.13
vmulsd xmm0, xmm10, QWORD PTR [24+r14] ;179.47
vunpcklpd xmm12, xmm14, xmm12 ;186.20
vaddsd xmm0, xmm0, QWORD PTR [24+r9] ;179.15
vunpcklpd xmm11, xmm13, xmm11 ;186.32
vaddsd xmm0, xmm0, xmm1 ;178.13
vsubpd xmm11, xmm12, xmm11 ;186.11
vmovupd XMMWORD PTR [1024+rbp], xmm11 ;186.11
vsubsd xmm11, xmm5, xmm0 ;186.11
vmovsd QWORD PTR [720+rbp], xmm5 ;182.13
vmovsd QWORD PTR [752+rbp], xmm0 ;178.13
vmovsd QWORD PTR [1040+rbp], xmm11 ;186.11
jmp .B1.13 ; Prob 100% ;186.11
.B1.12:: ; Preds .B1.8 .B1.9 .B1.10
mov rax, rsi ;182.25
mov rdx, QWORD PTR [896+rbp] ;182.13
imul rax, rdx ;182.25
imul rcx, rdx ;182.13
add rax, r9 ;182.13
mov QWORD PTR [1000+rbp], rcx ;182.13
sub rax, rcx ;182.13
mov rcx, QWORD PTR [920+rbp] ;182.13
imul r15, rcx ;182.13
mov QWORD PTR [960+rbp], rbx ;
mov rbx, rsi ;183.18
mov QWORD PTR [976+rbp], r15 ;182.13
sub rcx, r15 ;182.13
mov r15, QWORD PTR [928+rbp] ;182.13
imul rbx, r15 ;183.18
imul r12, r15 ;182.13
add rbx, r14 ;182.13
mov QWORD PTR [1008+rbp], r12 ;182.13
sub rbx, r12 ;182.13
mov r12, QWORD PTR [912+rbp] ;182.13
imul r11, r12 ;182.13
mov QWORD PTR [984+rbp], r11 ;182.13
sub r12, r11 ;182.13
mov r11, rsi ;184.18
mov QWORD PTR [992+rbp], r14 ;
mov r14, QWORD PTR [936+rbp] ;182.13
imul r11, r14 ;184.18
imul r10, r14 ;182.13
vmulsd xmm0, xmm10, QWORD PTR [r12+rbx] ;183.45
add r11, rdi ;182.13
vaddsd xmm0, xmm0, QWORD PTR [rcx+rax] ;183.15
mov QWORD PTR [968+rbp], r10 ;182.13
sub r11, r10 ;182.13
mov r10, QWORD PTR [904+rbp] ;182.13
imul r8, r10 ;182.13
mov QWORD PTR [944+rbp], rsi ;
lea rsi, QWORD PTR [-1+rsi] ;178.25
imul rdx, rsi ;178.25
imul r15, rsi ;179.18
imul r14, rsi ;180.18
sub r10, r8 ;182.13
add r9, rdx ;178.13
mov rdx, QWORD PTR [992+rbp] ;178.13
add rdi, r14 ;178.13
add rdx, r15 ;178.13
sub rdx, QWORD PTR [1008+rbp] ;178.13
sub r9, QWORD PTR [1000+rbp] ;178.13
sub rdi, QWORD PTR [968+rbp] ;178.13
mov QWORD PTR [888+rbp], rsi ;178.25
mov rsi, QWORD PTR [912+rbp] ;183.18
vmulsd xmm5, xmm8, QWORD PTR [r10+r11] ;184.49
mov r15, QWORD PTR [976+rbp] ;182.13
lea r14, QWORD PTR [rsi+rsi] ;183.18
sub r14, QWORD PTR [984+rbp] ;182.13
vaddsd xmm14, xmm0, xmm5 ;182.13
vmulsd xmm0, xmm10, QWORD PTR [rdx+r12] ;179.47
vmulsd xmm5, xmm8, QWORD PTR [rdi+r10] ;180.51
vaddsd xmm0, xmm0, QWORD PTR [r9+rcx] ;179.15
mov rcx, QWORD PTR [920+rbp] ;182.25
vaddsd xmm13, xmm0, xmm5 ;178.13
vmulsd xmm0, xmm10, QWORD PTR [r14+rbx] ;183.45
mov r10, QWORD PTR [904+rbp] ;184.18
lea r12, QWORD PTR [rcx+rcx] ;182.25
sub r12, r15 ;182.13
lea rcx, QWORD PTR [rcx+rcx*2] ;182.25
sub rcx, r15 ;182.13
lea r15, QWORD PTR [rsi+rsi*2] ;183.18
mov rsi, QWORD PTR [904+rbp] ;184.18
add r10, r10 ;184.18
sub r10, r8 ;182.13
sub r15, QWORD PTR [984+rbp] ;182.13
vmovsd QWORD PTR [704+rbp], xmm14 ;182.13
vmovsd QWORD PTR [736+rbp], xmm13 ;178.13
vmulsd xmm5, xmm8, QWORD PTR [r10+r11] ;184.49
vaddsd xmm0, xmm0, QWORD PTR [r12+rax] ;183.15
vaddsd xmm12, xmm0, xmm5 ;182.13
vmulsd xmm0, xmm10, QWORD PTR [r14+rdx] ;179.47
vmulsd xmm5, xmm8, QWORD PTR [r10+rdi] ;180.51
vaddsd xmm0, xmm0, QWORD PTR [r12+r9] ;179.15
vmovsd QWORD PTR [712+rbp], xmm12 ;182.13
lea r12, QWORD PTR [rsi+rsi*2] ;184.18
sub r12, r8 ;182.13
vaddsd xmm11, xmm0, xmm5 ;178.13
vmulsd xmm0, xmm10, QWORD PTR [r15+rbx] ;183.45
vmulsd xmm5, xmm8, QWORD PTR [r12+r11] ;184.49
vmulsd xmm1, xmm8, QWORD PTR [r12+rdi] ;180.51
vaddsd xmm0, xmm0, QWORD PTR [rcx+rax] ;183.15
vmovsd QWORD PTR [744+rbp], xmm11 ;178.13
vaddsd xmm5, xmm0, xmm5 ;182.13
vmulsd xmm0, xmm10, QWORD PTR [r15+rdx] ;179.47
vunpcklpd xmm12, xmm14, xmm12 ;186.20
vaddsd xmm0, xmm0, QWORD PTR [rcx+r9] ;179.15
vunpcklpd xmm11, xmm13, xmm11 ;186.32
vaddsd xmm0, xmm0, xmm1 ;178.13
vsubpd xmm11, xmm12, xmm11 ;186.11
vmovupd XMMWORD PTR [1024+rbp], xmm11 ;186.11
vsubsd xmm11, xmm5, xmm0 ;186.11
vmovsd QWORD PTR [720+rbp], xmm5 ;182.13
vmovsd QWORD PTR [752+rbp], xmm0 ;178.13
vmovsd QWORD PTR [1040+rbp], xmm11 ;186.11
mov rbx, QWORD PTR [960+rbp] ;186.11
mov rsi, QWORD PTR [944+rbp] ;186.11
.B1.13:: ; Preds .B1.12 .B1.11
3 つの文用に生成されたアセンブラー・コードは 214 命令でした。これらは、テザーを処理するループ内の一般的な文です。生成されたアセンブラー・コードの大部分でコンポーネントへのインデックスを計算しているのは、プログラマーが 1 以外のストライド参照のポインターを使用しているためです。
(ストライドがコンパイラーに対して既知の場合)
TOSVX1(3), TOSVX2(3), SUI(3)
(ストライドがコンパイラーに対して不明な場合)
rBeadIPIF(3,0:NBEAD+1), rBeadDIPIF(3,0:NBEAD+1), rBeadDDIPIF(3,0:NBEAD+1)
これらのインデックスは、すべてのテザーの各ビードに対して計算されます。
AOS で行われる倍精度浮動小数点演算にはすべて、スカラーが含まれます。
生成されたコードにはデータのストライドテストが含まれることにも注意してください。
cmp rax, 8 ;180.18
jne .B1.12 ; Prob 50% ;180.18
.B1.9:: ; Preds .B1.8
cmp QWORD PTR [912+rbp], 8 ;180.18
jne .B1.12 ; Prob 50% ;180.18
.B1.10:: ; Preds .B1.9
cmp QWORD PTR [904+rbp], 8 ;180.18
jne .B1.12 ; Prob 50% ;180.18
.B1.11:: ; Preds .B1.10
ストライドテストは、テストの結果に応じて 2 つの異なるコードパスの 1 つを使用します。
3 つの文の小さなループの PAOS アセンブラー・コード
mov r14, QWORD PTR [11184+rdi] ;172.15
mov r15, QWORD PTR [11176+rdi] ;172.15
imul r14, r15 ;
vmovupd ymm1, YMMWORD PTR [160+r13] ;204.10
vmovupd xmm2, XMMWORD PTR [32+rdi] ;178.94
vmovupd ymm0, YMMWORD PTR [_2il0floatpacket.40] ;
vmovupd YMMWORD PTR [576+r13], ymm1 ;204.10
vmovupd ymm1, YMMWORD PTR [_2il0floatpacket.39] ;
mov QWORD PTR [1432+rbp], r15 ;172.15
sub r14, r15 ;
mov r15, rsi ;176.15
mov r8, QWORD PTR [11200+rdi] ;172.15
imul r15, r8 ;176.15
mov r12, QWORD PTR [11208+rdi] ;172.15
imul r12, r8 ;
mov rax, QWORD PTR [11240+rdi] ;173.19
mov QWORD PTR [1528+rbp], rax ;173.19
mov rax, QWORD PTR [11328+rdi] ;173.19
mov QWORD PTR [1360+rbp], rax ;173.19
mov rax, QWORD PTR [11320+rdi] ;173.19
mov QWORD PTR [1408+rbp], rax ;173.19
mov rax, QWORD PTR [11304+rdi] ;173.19
mov r9, QWORD PTR [11120+rdi] ;172.15
add r15, r9 ;
mov QWORD PTR [1352+rbp], rax ;173.19
sub r15, r12 ;
mov rax, QWORD PTR [11296+rdi] ;173.19
sub r15, r14 ;
mov QWORD PTR [1400+rbp], r12 ;
mov r12, rsi ;176.15
mov r10, QWORD PTR [11080+rdi] ;172.15
mov QWORD PTR [1440+rbp], rax ;173.19
xor eax, eax ;173.19
imul r12, r10 ;176.15
mov rdx, QWORD PTR [11088+rdi] ;172.15
mov QWORD PTR [1416+rbp], r10 ;172.15
mov QWORD PTR [1392+rbp], r14 ;
imul rdx, r10 ;
mov r14, QWORD PTR [1352+rbp] ;
mov r10, QWORD PTR [1440+rbp] ;
imul r14, r10 ;
mov rbx, QWORD PTR [11064+rdi] ;172.15
sub r14, r10 ;
mov r11, QWORD PTR [11056+rdi] ;172.15
mov r10, rsi ;177.19
imul rbx, r11 ;
mov rcx, QWORD PTR [11000+rdi] ;172.15
add r12, rcx ;
sub rbx, r11 ;
sub r12, rdx ;
mov QWORD PTR [1448+rbp], r11 ;172.15
sub r12, rbx ;
mov r11, QWORD PTR [1408+rbp] ;
imul r10, r11 ;177.19
mov QWORD PTR [1496+rbp], r12 ;
mov r12, QWORD PTR [1360+rbp] ;
imul r12, r11 ;
mov QWORD PTR [1504+rbp], r15 ;
mov r15, QWORD PTR [1528+rbp] ;
add r10, r15 ;
sub r10, r12 ;
sub r10, r14 ;
mov QWORD PTR [1520+rbp], rax ;173.19
mov QWORD PTR [1488+rbp], r10 ;
mov QWORD PTR [1480+rbp], rax ;
mov QWORD PTR [1472+rbp], rax ;
mov QWORD PTR [1464+rbp], rax ;
mov QWORD PTR [1456+rbp], rax ;
mov QWORD PTR [1344+rbp], rcx ;
mov QWORD PTR [1352+rbp], r14 ;
mov QWORD PTR [1360+rbp], r12 ;
mov QWORD PTR [1368+rbp], rbx ;
mov QWORD PTR [1376+rbp], rdx ;
mov QWORD PTR [1384+rbp], r8 ;
mov QWORD PTR [1336+rbp], rsi ;
mov QWORD PTR [1320+rbp], rdi ;
mov rax, QWORD PTR [1456+rbp] ;
mov rdx, QWORD PTR [1464+rbp] ;
mov rcx, QWORD PTR [1472+rbp] ;
mov rbx, QWORD PTR [1480+rbp] ;
mov rsi, QWORD PTR [1488+rbp] ;
mov r8, QWORD PTR [1504+rbp] ;
mov r10, QWORD PTR [1520+rbp] ;
mov r11, QWORD PTR [1440+rbp] ;
mov r12, QWORD PTR [1432+rbp] ;
mov r14, QWORD PTR [1448+rbp] ;
vinsertf128 ymm2, ymm2, XMMWORD PTR [48+rdi], 1 ;178.94
mov rdi, QWORD PTR [1496+rbp] ;
ALIGN 16
.B1.6:: ; Preds .B1.6 .B1.5
vmovupd xmm10, XMMWORD PTR [rdx+rsi] ;178.63
vmovupd xmm3, XMMWORD PTR [rbx+r8] ;177.62
vmovupd xmm7, XMMWORD PTR [rcx+rdi] ;177.19
inc r10 ;173.19
vinsertf128 ymm11, ymm10, XMMWORD PTR [16+rdx+rsi], 1 ;178.63
add rdx, r11 ;173.19
vmulpd ymm12, ymm0, ymm11 ;178.63
vmulpd ymm13, ymm12, ymm2 ;178.94
vmulpd ymm15, ymm13, ymm2 ;178.94
vinsertf128 ymm4, ymm3, XMMWORD PTR [16+rbx+r8], 1 ;177.62
add rbx, r12 ;173.19
vmulpd ymm5, ymm1, ymm4 ;177.62
vmulpd ymm9, ymm5, ymm2 ;177.64
vinsertf128 ymm8, ymm7, XMMWORD PTR [16+rcx+rdi], 1 ;177.19
add rcx, r14 ;173.19
vaddpd ymm14, ymm8, ymm9 ;177.19
vaddpd ymm3, ymm14, ymm15 ;176.15
vmovupd YMMWORD PTR [256+r13+rax], ymm3 ;176.15
add rax, 32 ;173.19
cmp r10, 3 ;173.19
jb .B1.6 ; Prob 66% ;173.19
.B1.7:: ; Preds .B1.6
mov rsi, QWORD PTR [1336+rbp] ;
lea r11, QWORD PTR [-1+rsi] ;172.15
mov rax, QWORD PTR [1416+rbp] ;172.15
xor r10d, r10d ;173.19
imul rax, r11 ;172.15
vmovupd ymm0, YMMWORD PTR [_2il0floatpacket.40] ;
vmovupd ymm1, YMMWORD PTR [_2il0floatpacket.39] ;
mov rcx, QWORD PTR [1344+rbp] ;
add rcx, rax ;
mov rdx, QWORD PTR [1376+rbp] ;
sub rcx, rdx ;
mov r8, QWORD PTR [1384+rbp] ;
mov rdx, QWORD PTR [1408+rbp] ;173.19
imul rdx, r11 ;173.19
imul r8, r11 ;172.15
add r15, rdx ;
add r9, r8 ;
xor r8d, r8d ;
mov r12, QWORD PTR [1360+rbp] ;
sub r15, r12 ;
mov rbx, QWORD PTR [1368+rbp] ;
sub rcx, rbx ;
sub r9, QWORD PTR [1400+rbp] ;
xor ebx, ebx ;
mov QWORD PTR [1512+rbp], r10 ;173.19
xor edx, edx ;
mov r14, QWORD PTR [1352+rbp] ;
sub r15, r14 ;
mov QWORD PTR [1424+rbp], r11 ;172.15
mov rdi, QWORD PTR [1320+rbp] ;
sub r9, QWORD PTR [1392+rbp] ;
mov r11, QWORD PTR [1512+rbp] ;
mov r12, QWORD PTR [1440+rbp] ;
mov r14, QWORD PTR [1432+rbp] ;
mov rax, QWORD PTR [1448+rbp] ;
ALIGN 16
.B1.8:: ; Preds .B1.8 .B1.7
vmovupd xmm10, XMMWORD PTR [rbx+r15] ;174.65
vmovupd xmm3, XMMWORD PTR [r10+r9] ;173.64
vmovupd xmm7, XMMWORD PTR [r8+rcx] ;173.19
inc r11 ;173.19
vinsertf128 ymm11, ymm10, XMMWORD PTR [16+rbx+r15], 1 ;174.65
add rbx, r12 ;173.19
vmulpd ymm12, ymm0, ymm11 ;174.65
vmulpd ymm13, ymm12, ymm2 ;174.96
vmulpd ymm15, ymm13, ymm2 ;174.96
vinsertf128 ymm4, ymm3, XMMWORD PTR [16+r10+r9], 1 ;173.64
add r10, r14 ;173.19
vmulpd ymm5, ymm1, ymm4 ;173.64
vmulpd ymm9, ymm5, ymm2 ;173.66
vinsertf128 ymm8, ymm7, XMMWORD PTR [16+r8+rcx], 1 ;173.19
add r8, rax ;173.19
vaddpd ymm14, ymm8, ymm9 ;173.19
vaddpd ymm3, ymm14, ymm15 ;172.15
vmovupd YMMWORD PTR [352+r13+rdx], ymm3 ;172.15
add rdx, 32 ;173.19
cmp r11, 3 ;173.19
jb .B1.8 ; Prob 66% ;173.19
.B1.9:: ; Preds .B1.8
xor ecx, ecx ;173.19
xor edx, edx ;
.B1.10:: ; Preds .B1.10 .B1.9
vmovupd ymm1, YMMWORD PTR [256+r13+rdx] ;192.11
inc rcx ;173.19
vsubpd ymm2, ymm1, YMMWORD PTR [352+r13+rdx] ;192.11
vmovupd YMMWORD PTR [608+r13+rdx], ymm2 ;192.11
add rdx, 32 ;173.19
cmp rcx, 3 ;173.19
jb .B1.10 ; Prob 66% ;173.19
PAOS コードは、164 の命令 (および ALIGN 16 パディング用の NOP) を生成します。
以前のソースでは 1 つのループを 3 回反復していましたが、PAOS コードでは、TOSVX1、TOSVX2、SUI の結果をそれぞれ計算する 3 つのループを 3 回反復するようになりました。これらのループは比較的短く、大規模なインデックス計算はループエントリーの前に一度だけ行われます。実行パスは 98 命令増えて 4 つの SUI 結果で合計 262 命令、つまり SUI 結果あたり 65.5 命令になりました。1 つの SUI 結果で 214 の命令を生成した AOS 手法と比較すると、このコードセクションで約 3.26 倍スピードアップしたことになります。この概算はメモリーおよびキャッシュのレイテンシーを考慮していません。
倍精度浮動小数点のベクトル化は、大部分が 4 要素幅になりました。
vmovupd ymm1, YMMWORD PTR [160+r13] ;204.10
vmovupd xmm2, XMMWORD PTR [32+rdi] ;178.94
...
vmulpd ymm12, ymm0, ymm11 ;178.63
vmulpd ymm13, ymm12, ymm2 ;178.94
vmulpd ymm15, ymm13, ymm2 ;178.94
コンパイラーが上記のケースで 4 要素幅のロードを選択した理由は、分割キャッシュラインのロードの潜在的なペナルティーが、フェッチした変数を複数回再利用することによるパフォーマンス・ゲインよりも少ないと判断したためです。
一部のフェッチはまだ 2 ステップで行われ、
vmovupd xmm10, XMMWORD PTR [rbx+r15] ;174.65
...
vinsertf128 ymm11, ymm10, XMMWORD PTR [16+rbx+r15], 1 ;174.65
潜在的なキャッシュラインの分割ロードによるパフォーマンス低下を回避します。
コンパイラーはローカル一時変数 TOSVX1(3)、TOSVX2(3)、SUI(3) のアライメントを設定するため、これらの変数への 4 要素幅のアクセスではキャッシュラインの分割問題は発生しません。
PAOS には次の利点があります。
ビードごとにインデックス計算を行う点は同様ですが、テザー数は 1/4 です。
多くのフェッチとストアは 4 要素幅で、一部のみ 2 要素幅です。
倍精度の加算、減算、乗算は 4 要素幅です。
コードがより短いため L1 命令キャッシュがより効率良く利用されます。
(FORTRAN に詳しくない) C++ プログラマー向けの注意点
サンプルコードでは、配列へのポインターを使用しました。
AOS
real, pointer :: rBeadIPIF(:,:)
real, pointer :: rBeadDIPIF(:,:)
real, pointer :: rBeadDDIPIF(:,:)
...
rBeadIPIF => pFiniteSolution.rBeadIPIF
rBeadDIPIF => pFiniteSolution.rBeadDIPIF
rBeadDDIPIF => pFiniteSolution.rBeadDDIPIF
PAOS
type(TypeYMM), pointer :: rBeadIPIF(:,:)
type(TypeYMM), pointer :: rBeadDIPIF(:,:)
type(TypeYMM), pointer :: rBeadDDIPIF(:,:)
...
rBeadIPIF => pFiniteSolutionSIMD.rBeadIPIF
rBeadDIPIF => pFiniteSolutionSIMD.rBeadDIPIF
rBeadDDIPIF => pFiniteSolutionSIMD.rBeadDDIPIF
両バージョンとも、これらのポインターは、それぞれ pFiniteSolution および pFiniteSolutionSIMD 構造の配列全体を指します。これらも同様に配列へのポインターです。FORTRAN では、ポインターは連続しない配列部分を指すことができます。
real, pointer :: f(:,:)
type(TypeYMM), pointer :: t(:,:)
real, pointer:: slice(:,:)
...
s = 2 ! 3rd cell of 4-wide v(0:3)
slice(LBOUND(f, DIM=1):UBOUND(f, DIM=1), LBOUND(f, DIM=2):UBOUND(f, DIM=2)) => &
& t(LBOUND(f, DIM=1), LBOUND(f, DIM=2))%v(s::4)
f => slice
上記のソースで、ポインター f のストライドは 4 (double) で、pFiniteSolutionSIMD 構造の配列ポインターのストライドは 1 であると仮定し、v(s) を s=2 で開始しています。f では (3,0:NBEAD+1) のような 2 次元配列として表現され、インデックスは 4 要素幅ベクトルの 2 次元配列で、v 配列の列 s に付けられます。C++ プログラマーの皆さんは、なぜこんなことをする必要があるのか、疑問に思われることでしょう。
この疑問に答えるには、コードの 25% のみ PAOS を使用するように変換されたことを思い出してください。コードの残りの 75% はどうでしょうか。結局、ポインターとストライドが 1 でない代入を使用しても、コードの残りの 75% は、非 PAOS で割り当てられたすべての SIMD 割り当て配列を操作するまで変更できません。この機能により、アプリケーションの変換が偶然の産物になることはありません。FORTRAN のこの機能を使用しないと、複数のデータセットを続けて同期しなければなりません。
ストライドは 1 でない可能性があるため、FORTRAN コンパイラーは複数のコードパス (stride=1 の場合と stride != 1 の場合) を生成します。この文は修正するべきです。プロセッサーの命令セットが *1、*2、*4、*8 で配列セルをスケールできる場合、配列が言語の「自然な」数 (char、word、integer、float、double) であれば、上記のコードは正しくなります。Type(TypeYMM) 配列のケースでは、配列の各セルは 4 つの double (32 バイト) で構成されます。命令セットは *32 をスケールできないため、1 つの実行パスのみ生成されます。オーバーヘッドはほとんどありません。
add rdx, 32 ;173.19
C++ の等価コード
C++ プログラマーのために、等価な例を説明します。
struct xyz_t
{
double xyz[3];
};
struct FiniteSoluton_t
{
double rDELTIS;
int nBeads;
xyz_t* rBeadIPIF;
xyz_t* rBeadDIPIF;
xyz_t* rBeadDDIPIF;
FiniteSoluton_t()
{
nBeads = 0;
rBeadIPIF = NULL;
rBeadDIPIF = NULL;
rBeadDDIPIF = NULL;
}
void Allocate(int n)
{
if(rBeadIPIF) delete [] rBeadIPIF;
if(rBeadDIPIF) delete [] rBeadDIPIF;
if(rBeadDDIPIF) delete [] rBeadDDIPIF;
nBeads = n;
rBeadIPIF = new xyz_t[n];
rBeadDIPIF = new xyz_t[n];
rBeadDDIPIF = new xyz_t[n];
}
};
FiniteSoluton_t fs;
// dummy external function to force optimizer NOT to remove unused code
// *** this will generate a link error, ignore error and look at .ASM file
void foo(xyz_t& x);
void TENSEG(FiniteSoluton_t* pFiniteSolution)
{
int JSEG;
// pull in frequently used items from fs struct
int JSEGlast = pFiniteSolution->nBeads+1;
double rDELTIS = pFiniteSolution->rDELTIS;
xyz_t* rBeadIPIF = pFiniteSolution->rBeadIPIF;
xyz_t* rBeadDIPIF = pFiniteSolution->rBeadDIPIF;
xyz_t* rBeadDDIPIF = pFiniteSolution->rBeadDDIPIF;
xyz_t TOSVX1, TOSVX2, SUI;
for(JSEG=0; JSEG < JSEGlast; ++JSEG)
{
for(int i=0; i<3; ++i)
{
// Determine TUI at 1/2 integration step from now
// using current velocity and acceleration
// Position of X-End of segment
TOSVX1.xyz[i] = rBeadIPIF[JSEG].xyz[i]
+ (rBeadDIPIF[JSEG].xyz[i]*(rDELTIS/2.0))
+ (rBeadDDIPIF[JSEG].xyz[i]*(rDELTIS*rDELTIS/4.0));
// Position of Y-End of segment
TOSVX2.xyz[i] = rBeadIPIF[JSEG+1].xyz[i]
+ (rBeadDIPIF[JSEG+1].xyz[i]*(rDELTIS/2.0))
+ (rBeadDDIPIF[JSEG+1].xyz[i]*(rDELTIS*rDELTIS/4.0));
// SUI X->Y
SUI.xyz[i] = TOSVX2.xyz[i] - TOSVX1.xyz[i];
} // for(int i=0; i<3; ++i)
// insert code to assure optimizer does not remove loop
foo(SUI);
} // for(JSEG=0; JSEG < JSEGlast; ++JSEG)
}
PAOS コード
#include < dvec.h >
struct xyzF64vec4
{
F64vec4 xyz[3];
};
struct FiniteSolutonF64vec4
{
F64vec4 rDELTIS;
int nBeads;
xyzF64vec4* rBeadIPIF;
xyzF64vec4* rBeadDIPIF;
xyzF64vec4* rBeadDDIPIF;
FiniteSolutonF64vec4()
{
nBeads = 0;
rBeadIPIF = NULL;
rBeadDIPIF = NULL;
rBeadDDIPIF = NULL;
}
void Allocate(int n)
{
if(rBeadIPIF) delete [] rBeadIPIF;
if(rBeadDIPIF) delete [] rBeadDIPIF;
if(rBeadDDIPIF) delete [] rBeadDDIPIF;
nBeads = n;
rBeadIPIF = new xyzF64vec4[n];
rBeadDIPIF = new xyzF64vec4[n];
rBeadDDIPIF = new xyzF64vec4[n];
}
};
FiniteSolutonF64vec4 fsF64vec4;
// dummy external functon to force optimizer NOT to remove unused code
// *** this will generate a link error, ignore error and look at .ASM file
void foo(xyzF64vec4& x);
void TENSEG(FiniteSolutonF64vec4* pFiniteSolution)
{
int JSEG;
// pull in frequrently used items from fs struct
int JSEGlast = pFiniteSolution->nBeads+1;
F64vec4 rDELTIS = pFiniteSolution->rDELTIS;
xyzF64vec4* rBeadIPIF = pFiniteSolution->rBeadIPIF;
xyzF64vec4* rBeadDIPIF = pFiniteSolution->rBeadDIPIF;
xyzF64vec4* rBeadDDIPIF = pFiniteSolution->rBeadDDIPIF;
xyzF64vec4 TOSVX1, TOSVX2, SUI;
for(JSEG=0; JSEG < JSEGlast; ++JSEG)
{
for(int i=0; i<3; ++i)
{
// Determine TUI at 1/2 integration step from now
// using current velocity and acceleration
// Position of X-End of segment
TOSVX1.xyz[i] = rBeadIPIF[JSEG].xyz[i]
+ (rBeadDIPIF[JSEG].xyz[i]*(rDELTIS/2.0))
+ (rBeadDDIPIF[JSEG].xyz[i]*(rDELTIS*rDELTIS/4.0));
// Position of Y-End of segment
TOSVX2.xyz[i] = rBeadIPIF[JSEG+1].xyz[i]
+ (rBeadDIPIF[JSEG+1].xyz[i]*(rDELTIS/2.0))
+ (rBeadDDIPIF[JSEG+1].xyz[i]*(rDELTIS*rDELTIS/4.0));
// SUI X->Y
SUI.xyz[i] = TOSVX2.xyz[i] - TOSVX1.xyz[i];
} // for(int i=0; i<3; ++i)
// insert code to assure optimizer does not remove loop
foo(SUI);
} // for(JSEG=0; JSEG < JSEGlast; ++JSEG)
}
型宣言以外、コードセクションは同じです。
PAOS で変更するコードセクション
PAOS でプログラミングを行う場合、ソースコードを追加する必要があります。1 つの例は、ゼロ除算を回避するコードです。次に例を示します。
xyz_t& unitVector(xyz_t& v)
{
xyz_t ret;
double Length = sqrt(
v.xyz[0]*v.xyz[0]
+ v.xyz[1]*v.xyz[1]
+ v.xyz[2]*v.xyz[2]);
// defensive code to avoid divide by 0
// When (if) Length = 0.0 then substitute 1.0
// X = 0.0 / 1.0 = uX 0.0 (not divide by 0)
// Y = 0.0 / 1.0 = uY 0.0 (not divide by 0)
// Z = 0.0 / 1.0 = uZ 0.0 (not divide by 0)
if(Length == 0.0) Length = 1.0;
ret.xyz[0] = v.xyz[0] / Length;
ret.xyz[1] = v.xyz[1] / Length;
ret.xyz[2] = v.xyz[2] / Length;
return ret;
}
変更後:
xyzF64vec4& unitVector(xyzF64vec4& v)
{
xyzF64vec4 ret;
static const F64vec4 Zero(0.0);
static const F64vec4 One(1.0);
F64vec4 Length = sqrt(
v.xyz[0]*v.xyz[0]
+ v.xyz[1]*v.xyz[1]
+ v.xyz[2]*v.xyz[2]);
// defensive code to avoid divide by 0
// When (if) Length = 0.0 then substitute 1.0
// X = 0.0 / 1.0 = uX 0.0 (not divide by 0)
// Y = 0.0 / 1.0 = uY 0.0 (not divide by 0)
// Z = 0.0 / 1.0 = uZ 0.0 (not divide by 0)
Length = select_eq(Length, Zero, Length, One);
ret.xyz[0] = v.xyz[0] / Length;
ret.xyz[1] = v.xyz[1] / Length;
ret.xyz[2] = v.xyz[2] / Length;
return ret;
}
型宣言以外に、1 つの文のみ変更されています。
アセンブリー・コードにおける PAOS の利点
PAOS の実際の利点はアセンブリー・コードを見ると分かります。PAOS コードは一度に 4 つのエンティティーを処理しています。オリジナルの AOS コードと変更後の PAOS コードを比較してみましょう。ソースコードは同じです。唯一の違いはデータ型です。ソースコードを次に示します。
for(int i=0; i<3; ++i)
{
// Determine TUI at 1/2 integration step from now
// using current velocity and acceleration
// Position of X-End of segment
TOSVX1.xyz[i] = rBeadIPIF[JSEG].xyz[i]
+ (rBeadDIPIF[JSEG].xyz[i]*(rDELTIS/2.0))
+ (rBeadDDIPIF[JSEG].xyz[i]*(rDELTIS*rDELTIS/4.0));
// Position of Y-End of segment
TOSVX2.xyz[i] = rBeadIPIF[JSEG+1].xyz[i]
+ (rBeadDIPIF[JSEG+1].xyz[i]*(rDELTIS/2.0))
+ (rBeadDDIPIF[JSEG+1].xyz[i]*(rDELTIS*rDELTIS/4.0));
// SUI X->Y
SUI.xyz[i] = TOSVX2.xyz[i] - TOSVX1.xyz[i];
} // for(int i=0; i<3; ++i)
AOS アセンブリー・コード
;;; for(int i=0; i<3; ++i)
;;; {
;;;
;;; // Determine TUI at 1/2 integration step from now
;;; // using current velocity and acceleration
;;; // Position of X-End of segment
;;; TOSVX1.xyz[i] = rBeadIPIF[JSEG].xyz[i]
;;; + (rBeadDIPIF[JSEG].xyz[i]*(rDELTIS/2.0))
;;; + (rBeadDDIPIF[JSEG].xyz[i]*(rDELTIS*rDELTIS/4.0));
;;; // Position of Y-End of segment
;;; TOSVX2.xyz[i] = rBeadIPIF[JSEG+1].xyz[i]
vmulsd xmm1, xmm2, QWORD PTR [_2il0floatpacket.42] ;66.13
vmulsd xmm2, xmm2, xmm2 ;66.13
vmulsd xmm3, xmm2, QWORD PTR [_2il0floatpacket.43] ;66.13
vmovddup xmm0, xmm1 ;66.13
vmovddup xmm2, xmm3 ;66.13
vmovups XMMWORD PTR [80+rsp], xmm6 ;66.13
vmovapd xmm6, xmm2 ;66.13
vmovups XMMWORD PTR [64+rsp], xmm7 ;66.13
vmovapd xmm7, xmm1 ;66.13
vmovups XMMWORD PTR [48+rsp], xmm8 ;66.13
vmovapd xmm8, xmm3 ;66.13
vmovups XMMWORD PTR [32+rsp], xmm9 ;66.13
vmovapd xmm9, xmm0 ;66.13
mov QWORD PTR [136+rsp], rbx ;66.13
mov rbx, rax ;66.13
mov QWORD PTR [128+rsp], rsi ;66.13
mov rsi, rdx ;66.13
mov QWORD PTR [120+rsp], rdi ;66.13
mov rdi, rcx ;66.13
mov QWORD PTR [112+rsp], r12 ;66.13
mov r12, r8 ;66.13
mov QWORD PTR [104+rsp], r13 ;66.13
mov r13, r9 ;66.13
mov QWORD PTR [96+rsp], r14 ;66.13
mov r14, r10 ;66.13
.B5.3:: ; Preds .B5.4 .B5.2
vmulpd xmm4, xmm9, XMMWORD PTR [24+rbx+r12] ;66.13
vaddpd xmm5, xmm4, XMMWORD PTR [24+rbx+r13] ;66.13
vmulpd xmm4, xmm6, XMMWORD PTR [24+rbx+rdi] ;66.13
vaddpd xmm0, xmm5, xmm4 ;66.13
vmulpd xmm4, xmm9, XMMWORD PTR [rbx+r12] ;62.13
vmulpd xmm5, xmm6, XMMWORD PTR [rbx+rdi] ;62.13
vaddpd xmm4, xmm4, XMMWORD PTR [rbx+r13] ;62.13
vaddpd xmm4, xmm4, xmm5 ;62.13
;;; + (rBeadDIPIF[JSEG+1].xyz[i]*(rDELTIS/2.0))
;;; + (rBeadDDIPIF[JSEG+1].xyz[i]*(rDELTIS*rDELTIS/4.0));
;;; // SUI X->Y
;;; SUI.xyz[i] = TOSVX2.xyz[i] - TOSVX1.xyz[i];
vsubpd xmm4, xmm0, xmm4 ;70.11
vmovupd XMMWORD PTR [144+rsp], xmm4 ;70.11
;;; } // for(int i=0; i<3; ++i)
lea rcx, QWORD PTR [144+rsp] ;73.3
vmulsd xmm4, xmm7, QWORD PTR [40+rbx+r12] ;66.13
vmulsd xmm5, xmm8, QWORD PTR [40+rbx+rdi] ;66.13
vaddsd xmm4, xmm4, QWORD PTR [40+rbx+r13] ;66.13
vaddsd xmm0, xmm4, xmm5 ;66.13
vmulsd xmm4, xmm7, QWORD PTR [16+rbx+r12] ;62.13
vmulsd xmm5, xmm8, QWORD PTR [16+rbx+rdi] ;62.13
vaddsd xmm4, xmm4, QWORD PTR [16+rbx+r13] ;62.13
vaddsd xmm4, xmm4, xmm5 ;62.13
vsubsd xmm4, xmm0, xmm4 ;70.11
vmovsd QWORD PTR [160+rsp], xmm4 ;70.11
AOS では、2 要素幅のベクトルとスカラー命令を使用して、46 命令で 1 つの SUI ベクトルが計算されました。このループはアンロールされました。
PAOS アセンブリー・コード
;;; for(int i=0; i<3; ++i)
;;; {
;;;
;;; // Determine TUI at 1/2 integration step from now
;;; // using current velocity and acceleration
;;; // Position of X-End of segment
;;; TOSVX1.xyz[i] = rBeadIPIF[JSEG].xyz[i]
vdivpd ymm1, ymm0, YMMWORD PTR [_2il0floatpacket.437] ;213.13
vmulpd ymm0, ymm0, ymm0 ;213.13
vmovupd YMMWORD PTR [288+r13], ymm1 ;213.13
vdivpd ymm0, ymm0, YMMWORD PTR [_2il0floatpacket.438] ;213.13
vmovupd YMMWORD PTR [320+r13], ymm0 ;213.13
mov QWORD PTR [456+rsp], rbx ;213.13
mov rbx, rax ;213.13
mov QWORD PTR [448+rsp], rsi ;213.13
mov rsi, rdx ;213.13
mov QWORD PTR [440+rsp], rdi ;213.13
mov rdi, rcx ;213.13
mov QWORD PTR [432+rsp], r12 ;213.13
mov r12, r8 ;213.13
mov QWORD PTR [424+rsp], r14 ;213.13
mov r14, r9 ;213.13
mov QWORD PTR [416+rsp], r15 ;213.13
mov r15, r10 ;213.13
.B5.3:: ; Preds .B5.4 .B5.2
vmovupd ymm4, YMMWORD PTR [288+r13] ;213.13
;;; + (rBeadDIPIF[JSEG].xyz[i]*(rDELTIS/2.0))
;;; + (rBeadDDIPIF[JSEG].xyz[i]*(rDELTIS*rDELTIS/4.0));
;;; // Position of Y-End of segment
;;; TOSVX2.xyz[i] = rBeadIPIF[JSEG+1].xyz[i]
;;; + (rBeadDIPIF[JSEG+1].xyz[i]*(rDELTIS/2.0))
;;; + (rBeadDDIPIF[JSEG+1].xyz[i]*(rDELTIS*rDELTIS/4.0));
;;; // SUI X->Y
;;; SUI.xyz[i] = TOSVX2.xyz[i] - TOSVX1.xyz[i];
;;; } // for(int i=0; i<3; ++i)
;;; // insert code to assure optimizer does not remove loop
;;; foo(SUI);
lea rcx, QWORD PTR [192+r13] ;224.3
vmovupd ymm3, YMMWORD PTR [320+r13] ;213.13
vmulpd ymm5, ymm4, YMMWORD PTR [rbx+r12] ;213.13
vmulpd ymm1, ymm3, YMMWORD PTR [rbx+rdi] ;213.13
vaddpd ymm0, ymm5, YMMWORD PTR [rbx+r14] ;213.13
vmulpd ymm5, ymm4, YMMWORD PTR [96+rbx+r12] ;217.13
vaddpd ymm2, ymm0, ymm1 ;213.13
vmulpd ymm1, ymm3, YMMWORD PTR [96+rbx+rdi] ;217.13
vmovupd YMMWORD PTR [r13], ymm2 ;213.13
vaddpd ymm0, ymm5, YMMWORD PTR [96+rbx+r14] ;217.13
vaddpd ymm5, ymm0, ymm1 ;217.13
vsubpd ymm2, ymm5, ymm2 ;221.11
vmovupd YMMWORD PTR [96+r13], ymm5 ;217.13
vmovupd YMMWORD PTR [192+r13], ymm2 ;221.11
vmulpd ymm0, ymm4, YMMWORD PTR [32+rbx+r12] ;213.13
vmulpd ymm2, ymm3, YMMWORD PTR [32+rbx+rdi] ;213.13
vmulpd ymm5, ymm4, YMMWORD PTR [128+rbx+r12] ;217.13
vaddpd ymm1, ymm0, YMMWORD PTR [32+rbx+r14] ;213.13
vaddpd ymm0, ymm5, YMMWORD PTR [128+rbx+r14] ;217.13
vaddpd ymm1, ymm1, ymm2 ;213.13
vmulpd ymm2, ymm3, YMMWORD PTR [128+rbx+rdi] ;217.13
vmovupd YMMWORD PTR [32+r13], ymm1 ;213.13
vaddpd ymm5, ymm0, ymm2 ;217.13
vsubpd ymm1, ymm5, ymm1 ;221.11
vmovupd YMMWORD PTR [128+r13], ymm5 ;217.13
vmovupd YMMWORD PTR [224+r13], ymm1 ;221.11
vmulpd ymm0, ymm4, YMMWORD PTR [64+rbx+r12] ;213.13
vmulpd ymm2, ymm3, YMMWORD PTR [64+rbx+rdi] ;213.13
vmulpd ymm4, ymm4, YMMWORD PTR [160+rbx+r12] ;217.13
vmulpd ymm3, ymm3, YMMWORD PTR [160+rbx+rdi] ;217.13
vaddpd ymm1, ymm0, YMMWORD PTR [64+rbx+r14] ;213.13
vaddpd ymm0, ymm1, ymm2 ;213.13
vaddpd ymm1, ymm4, YMMWORD PTR [160+rbx+r14] ;217.13
vmovupd YMMWORD PTR [64+r13], ymm0 ;213.13
vaddpd ymm1, ymm1, ymm3 ;217.13
vsubpd ymm0, ymm1, ymm0 ;221.11
vmovupd YMMWORD PTR [160+r13], ymm1 ;217.13
vmovupd YMMWORD PTR [256+r13], ymm0 ;221.11
PAOS は、4 要素幅のベクトルをすべて使用して一度に (4 つの異なるテザーの) 4 つのセグメントを計算します。for ループはアンロールされ、生成されたコードは 4 つの SUI 結果を 56 命令で計算しました。1 つの SUI 結果あたりの命令数は 56/4 = 14 となります。
AOS では 46 命令で 1 つの SUI を計算したのに対して、PAOS では 14 命令で 1 つの SUI を計算しました。命令あたりの時間が等しいと仮定すると、(このコードサンプルでは) PAOS は AOS に対して 3.28 倍パフォーマンスが向上したことになります。
注意: アプリケーション全体で実際に 3.28 倍パフォーマンスが向上すると仮定しないでください。
すべてのアプリケーションで AOS から PAOS が使用できるとは限りませんが、アプリケーションの一部は変換によるメリットを得られるでしょう。この後、テザーシステム研究用の FORTRAN アプリケーションで PAOS に変換したコードを使用した結果を紹介します。このアプリケーションでは、コードの 25% のみを PAOS に変更しました (大部分はコピー・アンド・ペースト、検索、置換)。宇宙船は 96 のテザーのコレクションで相互接続されます。この設定では、パフォーマンスの向上は 2 倍になります。上記のコードの 3.28 倍には届きませんが、プログラミングに時間をかけるだけの価値はあるといえるでしょう。
プログラム変換手法
テザー・シミュレーション・プログラムでは、“type TypeFiniteSolution” の本体を別のファイル (FiniteSolution.inc) に分割しました。型定義を含むモジュールのコンパイルには、FORTRAN プリプロセッサー (FPP) を使用します。
! Note, "real" is not defined at this point
! i.e. "real" in the FPP #include file passes through as "real"
type TypeFiniteSolution
SEQUENCE
#include "FiniteSolution.inc"
! No additional data to the original type
end type TypeFiniteSolution
! XMM, YMM and YMM02 variants replace "real" with
! "type(TypeXMM)", "type(TypeYMM)" and "type(TypeYMM02)"
! XMM variant
#define real type(TypeXMM)
type TypeFiniteSolutionXMM
SEQUENCE
#include "FiniteSolution.inc"
! additional members for TypeXMM
integer :: TetherNumber0
integer :: TetherNumber1
end type TypeFiniteSolutionXMM
#undef real
! YMM variant
#define real type(TypeYMM)
type TypeFiniteSolutionYMM
SEQUENCE
#include "FiniteSolution.inc"
! additional members for TypeYMM
integer :: TetherNumber0
integer :: TetherNumber1
integer :: TetherNumber2
integer :: TetherNumber3
end type TypeFiniteSolutionYMM
#undef real
! YMM02 variant
#define real type(TypeYMM02)
type TypeFiniteSolutionYMM02
SEQUENCE
#include "FiniteSolution.inc"
! additional members for TypeYMM02
integer :: TetherNumber0
integer :: TetherNumber1
integer :: TetherNumber2
end type TypeFiniteSolutionYMM02
#undef real
FPP を使用して “real” を適切な型に再定義することにより、同じ手法をサブルーチンと関数に使用できます。非 SIMD では通常、サフィックス “.v” は含まれないため、SIMD 型変数の影響を受けるサブルーチンと関数では 2 つのバージョンが必要になります。
ジェネリック・サブルーチンと関数のインターフェイス
ジェネリック・サブルーチンと関数のインターフェイスの使用は、PAOS への変換の主な要件です。次元 3 の 2 つの配列の CROSS 積の要件について見てみましょう。
interface CROSS
RECURSIVE SUBROUTINE CROSS_r_r_r(VA,VB,VC)
use MOD_ALL
real :: VA(3), VB(3), VC(3)
END SUBROUTINE CROSS_r_r_r
RECURSIVE SUBROUTINE CROSS_r_r_ymm(VA,VB, VC)
USE MOD_ALL
real :: VA(3), VB(3)
type(TypeYMM) :: VC(3)
END SUBROUTINE CROSS_r_r_ymm
RECURSIVE SUBROUTINE CROSS_r_r_ymm02(VA,VB, VC)
USE MOD_ALL
real :: VA(3), VB(3)
type(TypeYMM02) :: VC(3)
END SUBROUTINE CROSS_r_r_ymm02
RECURSIVE SUBROUTINE CROSS_r_r_xmm(VA,VB, VC)
USE MOD_ALL
real :: VA(3), VB(3)
type(TypeXMM) :: VC(3)
END SUBROUTINE CROSS_r_r_xmm
RECURSIVE SUBROUTINE CROSS_ymm_ymm_ymm(VA,VB,VC)
use MOD_ALL
type(TypeYMM) :: VA(3), VB(3), VC(3)
END SUBROUTINE CROSS_ymm_ymm_ymm
RECURSIVE SUBROUTINE CROSS_ymm02_ymm02_ymm02(VA,VB,VC)
use MOD_ALL
type(TypeYMM02) :: VA(3), VB(3), VC(3)
END SUBROUTINE CROSS_ymm02_ymm02_ymm02
RECURSIVE SUBROUTINE CROSS_xmm_xmm_xmm(VA,VB, VC)
use MOD_ALL
type(TypeXMM) :: VA(3), VB(3), VC(3)
END SUBROUTINE CROSS_xmm_xmm_xmm
end interface CROSS
一般的なアプリケーションでは、さまざまな (すべてではない) 引数の型が置換されることに注意してください。この処理にはジェネリック・サブルーチン・インターフェイスを使用します。
! EVAL ANGULAR MOMENTUM DERIVATIVE TERM
CALL CROSS (RPI,RPIDD, pFiniteSolutionSIMD.rRVDI)
上記では CROSS_r_r_ymm を呼び出します。
! FORM VECTOR IN DIRECTION OF TETHER FRAME "K" UNIT VECTOR
CALL CROSS (pFiniteSolutionSIMD.rUITI, pFiniteSolutionSIMD.rUJOI, pFiniteSolutionSIMD.rUKTI)
上記では CROSS_ymm_ymm_ymm を呼び出します。
各サブルーチンは、異なる PAOS 幅 (2 要素幅、3 要素幅、4 要素幅) 用にオリジナルの AOS レイアウトをコピーしたものです。この点は、テンプレートを使用できる C++ のほうが楽です。FORTRAN の場合、Visual Studio* でサブルーチンを選択して、サブルーチンのコンテンツをすべて選択し、クリップボードにコピーします。ソリューション・エクスプローラーでプロジェクトをクリックして、項目の追加を選択し、オリジナルの名前にサフィックス (ここでは、ymm、ymm02、xmm を使用) を加えたファイルを追加します。そして、オリジナルのサブルーチンのコンテンツを新しい空のファイルに貼り付けます。残りのステップは、型の変更と適切な USE モジュールの追加です。
データの変更についても考慮する必要があります。FORTRAN で演算子関数を使用すれば、変数のサフィックス “.v” を検索および置換して削除できますが、コンパイラーがコードをインライン展開しなくなるため、今回はその方法を採用していません。このインライン問題は、この記事が掲載される頃には製品アップデートで解消される予定です。
コードセクションの一部は、PAOS ベクトルを水平にアドレスする必要があります。すべての異なる PAOS 幅で同じコードテキストになるように、FORTRAN サブルーチンに次のコードを追加します。
integer :: s
integer, parameter :: sLast = 3
以下のように使用しました。
! FORM UNIT VECTOR FROM X-END TO Y-END OF BEAD SEGMENT
do s=0,sLast
if(DUMEL.v(s) .ne. 0.0_8) then
TUI.v(s) = SUI.v(s) / DUMEL.v(s)
else
call RandomUnitVector(TUI.v(s))
endif
end do
(“parameter” は C++ の “static const” のようなものです)
上記のコードは、NULL ベクトルを返す代わりに任意の単位ベクトルを返すことを除いてゼロ除算を回避しています。上記の変更は AOS (非 PAOS) として動作します。
NULL ベクトルを生成する場合、コードは次のようになります。
RadiusSquared.v = RelativePOSE_IF(1).v**2 &
& + RelativePOSE_IF(2).v**2 &
& + RelativePOSE_IF(3).v**2
! N.B we are comparing a bead position within a tether against
! a gravitational body position they should not coincide
! ignore if at center of object
!DEC$ VECTOR ALWAYS
do s = 0, sLast
if(RadiusSquared.v(s) .eq. 0.0_8) RadiusSquared.v(s) = 1.0_8
end do
Radius.v = dsqrt(RadiusSquared.v)
ACCE_IFlocal(1).v = RelativePOSE_IF(1).v &
& * ((pObject.rGMft3Ps2 / RadiusSquared.v) / Radius.v)
ACCE_IFlocal(2).v = RelativePOSE_IF(2).v &
& * ((pObject.rGMft3Ps2 / RadiusSquared.v) / Radius.v)
ACCE_IFlocal(3).v = RelativePOSE_IF(3).v &
& * ((pObject.rGMft3Ps2 / RadiusSquared.v) / Radius.v)
上記のコードに関する最適化の注意点
ゼロ除算を回避するコードは、ベクトルの 2 乗をテストするために移動されています。パスにかかわらず結果は同じになりますが、dsqrt が 0.0 の平方根を実行することはありません。プロセッサーのマイクロコードに応じて、0.0 の平方根のパスは長くなります。
上記の s ループ (定数 sLast) はアンロールおよびベクトル化されます。このループは分岐命令なしで完全にベクトル化されます。
AOS に対する PAOS の利点
AOS は、NumberOfBeads に関連して割り当てられる大きな配列をベクトル化できますが、次元 (3) および (3,3) の小さな固定配列をベクトル化する可能性は限定的で、スカラー操作はベクトル化できません。PAOS は、スカラー、そして次元 (3) および (3,3) の小さな固定配列も完全にベクトル化でき、NumberOfBeads に関連して割り当てられる大きな配列をベクトル化する可能性も高くなります。
スカラー計算の利点
各テザーで繰り返される従来の非 SIMD 文
! CALCULATE 1ST TERM ! AND ACCUMULATE THIS INCREMENT DUMSCL = DUMCEE * ( 2.0_8*(pFiniteSolution%rELD / pFiniteSolution%rEL)**2 & & - pFiniteSolution%rELDD / pFiniteSolution%rEL )
4 つのテザーのグループで繰り返される SIMD 文
! CALCULATE 1ST TERM ! AND ACCUMULATE THIS INCREMENT DUMSCL.v = DUMCEE.v * ( 2.0_8*(pFiniteSolution%rELD.v / pFiniteSolution%rEL.v)**2 & & - pFiniteSolution%rELDD.v / pFiniteSolution%rEL.v )
コードが少しだけ変更されていることに注意してください。一部のコードは変数 TypeYMM、TypeXMM、TypeYMM02 にサフィックス “.v” を追加して使用されています。このサフィックスは演算子関数を宣言すると削除できますが (後述)、デバッグビルドでコードをインライン展開するために、ここではサフィックスを使用しています。これらのコード変更は、検索と置換を使用して行うことができます。プログラマーが演算子の多重定義関数を使用することを決めた場合、(型宣言以外に) コードを変更する必要はありません。
小さな固定配列による計算の利点
小さな固定サイズの配列の処理は、PAOS の利点の 1 つです。テザーの先端と終端の位置を考慮して、先端と終端間のベクトルおよび先端と終端間の単位ベクトルを計算するとします (コードが読みやすいように pFiniteSolution% ポインターは削除しています)。
real(8) :: Front(3), Back(3), ELI(3), UELI(3), Length
ELI(1) = Back(1) – Front(1)
ELI(2) = Back(2) – Front(2)
ELI(3) = Back(3) – Front(3)
Length = DSQRT(ELI(1)**2 + ELI(2)**2 + ELI(3)**2)
UEIL(1) = ELI(1) / Length
UEIL(2) = ELI(2) / Length
UEIL(3) = ELI(3) / Length
スカラー AOS コードは、上記のコードの部分のみをベクトル化できます。SSE プラットフォームでは、Back と Front の 3 つのコンポーネントのうち 2 つのみを一度にロードして減算できます。3 つ目のコンポーネントは別にロードして減算します。“ELI(1)**2 + ELI(2)**2” は 1 つの操作で行うことができますが、“ELI(3)**2” は別の操作になります。残りの問題は、SSE では “ELI(1)**2 + ELI(2)**2” の結果の水平加算をした後に “ELI(3)**2” の追加スカラー加算を実行しなければならないことです。その後、スカラー DSQRT 操作を実行して Length を生成します。スカラーによる ELI(1:3) の除算は、“ELI(1) + ELI(2)” (2 要素幅) と “ELI(3)” コンポーネントの 2 つのステップで行われます。ストアは、ロードのときに説明した 2 つのステップで行われます。
AVX システムでは、コードは var(1:2) と var(3) の 2 つの部分で (YMM レジスターの 4 番目の要素をあらかじめクリアする XOR を追加して) Back と Front をそれぞれロードします。減算は、“ELI(1)**2 + ELI(2)**2 + ELI(3)**2” の 2 乗と同じように、1 つの操作で行われます。しかし、この時点では、AVX コードは 3 つの部分的な結果を水平加算した後にスカラー DSQRT を実行して Length を生成する必要があります。Length による ELI の除算は、YMM レジスターに Length をブロードキャストした後に 1 つの操作で行われます。通常、YMM レジスターの 4 番目の要素が未定義であることが確実でないため、この操作は 1 ステップではなく、2 要素幅、1 要素幅の 2 つのステップで行われます。ロードとストアが、2 つの部分で YMM レジスターの 4 番目の要素をあらかじめクリアする XOR を追加してそれぞれ実行されていることに注意してください。
PAOS は容易にすべてのコードを完全にベクトル化できる
type(TypeYMM) :: Front(3), Back(3), ELI(3), UELI(3), Length
ELI(1).v = Back(1).v – Front(1).v
ELI(2).v = Back(2).v – Front(2).v
ELI(3).v = Back(3).v – Front(3).v
Length.v = DSQRT(ELI(1).v**2 + ELI(2).v**2 + ELI(3).v**2)
UEIL(1).v = ELI(1).v / Length.v
UEIL(2).v = ELI(2).v / Length.v
UEIL(3).v = ELI(3).v / Length.v
最初の文で、ELI ベクトルの各要素は 4 要素幅で計算されます (一度に 4 テザー)。部分的な結果は別の 4 要素幅の YMM レジスターで保存されます。2 乗は、各 4 要素幅の 3 つの異なるレジスターで実行されます。3 つの要素の水平加算が、3 つの 4 要素幅の要素の垂直加算になりました。次に、2 乗の 4 要素幅の合計に DSQRT が実行されます (Sandy Bridge では YMM レジスターの半分に DSQRT が内部的に実行され、Ivy Bridge では 4 要素幅の DSQRT が実行されます)。生成された 4 要素幅の長さ (個別の値) は、4 つの単位ベクトルの生成に使用されます。上記のコードは完全な 4 要素幅 SIMD で、1 つのテザーよりも 4 つのテザーでより高速に実行されます (速度はキャッシュラインがどこで分割されるかに依存します)。
大きな配列の利点
大きな配列のループを実行すると、配列が 3 つの (X、Y、Z) コンポーネントを含む場合と同様の利点が得られます。PAOS データフロー計算は次のようになります。
OBJECT(1)%X(1) | OBJECT(2)%X(1) | OBJECT(3)%X(1) | OBJECT(4)%X(1) OBJECT(1)%Y(1) | OBJECT(2)%Y(1) | OBJECT(3)%Y(1) | OBJECT(4)%Y(1) OBJECT(1)%Z(1) | OBJECT(2)%Z(1) | OBJECT(3)%Z(1) | OBJECT(4)%Z(1) OBJECT(1)%X(2) | OBJECT(2)%X(2) | OBJECT(3)%X(2) | OBJECT(4)%X(2) OBJECT(1)%Y(2) | OBJECT(2)%Y(2) | OBJECT(3)%Y(2) | OBJECT(4)%Y(2) OBJECT(1)%Z(2) | OBJECT(2)%Z(2) | OBJECT(3)%Z(2) | OBJECT(4)%Z(2)
OBJECT は、アプリケーション・ベクトルの配列を含み、3 ユニットの SIMD 4 要素幅ベクトルに格納された SIMD 4 要素幅ベクトルへ再マップされた構造を表します。
スカラー (オリジナル) 表現
! Position with respect to IP IF
real, pointer :: rBeadIPIF(:,:) ! (3,NumberOfBeads+2)
AVX 4 要素幅 SIMD 表現
! Position with respect to IP IF
type(TypeYMM), pointer :: rBeadIPIF(:,:) ! (3,NumberOfBeads+2)
隣接するビード間のベクトルおよびそのベクトルの単位ベクトルを生成するコード。
部分的なベクトル化を含めて最適化するオリジナルのコード (一部):
DO I=1,nBeads
ELI(1) = pFiniteSolution%rBeadIPIF(1,I) – pFiniteSolution%rBeadIPIF(1,I+1)
ELI(2) = pFiniteSolution%rBeadIPIF(2,I) – pFiniteSolution%rBeadIPIF(2,I+1)
ELI(3) = pFiniteSolution%rBeadIPIF(3,I) – pFiniteSolution%rBeadIPIF(3,I+1)
Length = DSQRT(ELI(1)**2 + ELI(2)**2 + ELI(3)**2)
pFiniteSolution%rTUI(1,I) = ELI(1) / Length
pFiniteSolution%rTUI(2,I) = ELI(2) / Length
pFiniteSolution%rTUI(3,I) = ELI(3) / Length
END DO
4 つのテザーを完全にベクトル化する YMM SIMD コード:
DO I=1,nBeads
ELI(1).v = pFiniteSolution%rBeadIPIF(1,I).v – pFiniteSolution%rBeadIPIF(1,I+1).v
ELI(2).v = pFiniteSolution%rBeadIPIF(2,I).v – pFiniteSolution%rBeadIPIF(2,I+1).v
ELI(3).v = pFiniteSolution%rBeadIPIF(3,I).v – pFiniteSolution%rBeadIPIF(3,I+1).v
Length = DSQRT(ELI(1).v**2 + ELI(2).v**2 + ELI(3).v**2).v
pFiniteSolution%rTUI(1,I).v = ELI(1).v / Length
pFiniteSolution%rTUI(2,I).v = ELI(2).v / Length
pFiniteSolution%rTUI(3,I).v = ELI(3).v / Length
END DO
SOA に対する利点
SOA レイアウトでは、PAOS よりも多くのキャッシュラインのロードと TLB ロードが必要です。例えば、テザーのビード間のベクトルと単位ベクトルを生成するケースです。SOA では、以下の個別のキャッシュラインおよび TLB が必要です。
rBeadIPIF(I,1,t) rBeadIPIF(I+1,1,t) (8 分割のキャッシュライン) rBeadIPIF(I,2,t) rBeadIPIF(I+1,2,t) (8 分割のキャッシュライン) rBeadIPIF(I,3,t) rBeadIPIF(I+1,3,t) (8 分割のキャッシュライン) rTUI(I,1,t) (8 分割のキャッシュライン) rTUI(I,2,t) (8 分割のキャッシュライン) rTUI(I,3,t) (8 分割のキャッシュライン)
各テザーのビードごとに 6 つのキャッシュラインが必要です。
PAOS では、一度に 4 つのテザーのビードごとに 4 つのキャッシュラインが必要です。
rBeadIPIF(1,I).v(0:3) rBeadIPIF(1,I+1).v(0:3) (↓ とキャッシュラインを共有) rBeadIPIF(2,I).v(0:3) rBeadIPIF(2,I+1).v(0:3) (上記/下記の半分) rBeadIPIF(3,I).v(0:3) rBeadIPIF(3,I+1).v(0:3) (↑ とキャッシュラインを共有) rTUI(1,I).v(0:3) (↓ とキャッシュラインを共有) rTUI(2,I).v(0:3) (上記/下記の半分) rTUI(3,I).v(0:3) (↑ とキャッシュラインを共有)
PAOS はキャッシュラインを高速にトラバース (高速にフラッシュ) しますが、(SIMD は 4 つのテザーをデータにパックするため) トラバースは 1/4 になります。合計のデータストレージが両方のレイアウトで同じであれば、個別のキャッシュラインおよび TLB エントリーに関する要求は減ります。
ベンチマーク・プログラム
PAOS の利点を説明するため、ベンチマークを使用して実際のアプリケーションと比較しましょう。ベンチマークには、よく知られている複雑なシミュレーション・プログラムを使用しました。これまで 7 年間にわたりコードの最適化を繰り返してきた結果、PAOS への変換前は、コードを改良できる部分はほとんど残されていないと私は考えていました。コードの大部分は容易にベクトル化できないことが分かっていたからです。また、コンパイラーによりベクトル化および最適化されるコードをすべてベクトル化できるとは限らないことも分かっていました。
この状況を打破するために、このアプリケーション用に開発されたのがパックド構造体配列です。SOA 形式も考えましたが、このアプリケーションではあまり効果がないことが分かっていました。
このプログラムは、宇宙船に接続されたテザーのシミュレーション用に高度に最適化された OpenMP* FORTRAN プログラムで、宇宙エレベーター設計問題の調査にも使用されています。ベンチマークとして、EDDE 宇宙船のシミュレーション研究構成を選択しました。この宇宙船は、衛星軌道近くのデブリ (人工衛星の残骸などの宇宙ゴミ) を除去するために提案されたものです。

EDDE 宇宙船 の構成は、これまで説明したテザー衛星よりも長く大規模になります。
ペイロード・マネージャー x 2
コントローラー/エミッター x 2
太陽電池 x 9
ペイロード・マネージャーとコントローラー/エミッターを接続する短いテザー (~15 m) x 2
アルミテープの長いテザー (各 1 km) x 10
合計 12 個のテザーで 13 個のサテライトを接続します。
PAOS に変換したのは、アプリケーションのテザー部分の有限要素部分のみです。この部分は重要ですが、コードの一部にすぎません (~25%)。残りのテザー部分とボディー部分 (ペイロード・マネージャー、コントローラー/エミッター、太陽電池、地球、月、惑星、その他) はまだ PAOS に変換されていないため、PAOS の利点は完全には引き出されていません。
このプログラムの Visual Studio* ソリューションには、12 の FORTRAN プロジェクトと 1 つの C++ プロジェクトが含まれています。C++ プロジェクトは、プロセッサーがサポートする SIMD 関数を調べるために使用されます。合計 554 個の F90 ソースファイルが使用され、それらの多くには複数のサブルーチンと関数が含まれています。PAOS をサポートするため、オリジナルのソリューションに約 100 個のファイルが追加されました。これらのファイルのコンテンツは、表面上は、オリジナルのソースにサフィックス “.v” と、異なる SIMD パック形式用の異なるデータ型を追加したものと同じです。
テストは、インテル® Core™ i7 2600K プロセッサー (4 コア、インテル® ハイパースレッディング (HT) テクノロジー対応、開発コード名 Sandy Bridge)、Windows* 7 Professional (64 ビット)、16GB RAM のシステムで行われました。
システムは、HT をオン/オフ、ターボブーストをオン/オフにしました。今回は 4 コア・プロセッサーのシステムを使用したため、テストは主に HT オフで実行され、アプリケーションで倍精度浮動小数点を多用しました。
コードの多くの部分はボディーの処理を行っていたため (非 PAOS コードの約 80%)、テザーのシミュレーションでは要素 (テザー) 数を増やしました。テザーあたりのビード数は 1,000 から 10,000 に増やしました。テザーあたりのビード数を 10 倍にすると、PAOS コードに対する非 PAOS コードの相対的な負荷は 1/10 になります。さらにビード数を増やすこともできましたが、テスト結果で PAOS の使用にバイアスをかけすぎないように、この値に決めました。
負荷バランスをとるため、両端の 2 つの短いテザー (各 15 m) を 1 km のアルミのテザー (10,000 ビード) に置き換え、12 個のテザーすべてが同じデザインと統合オプションになるようにしました。
このアプリケーションでは、同じビード数と同じ統合オプション (空気力学、電気力学、その他) のテザーが SIMD PAOS レイアウトへの統合に適しています。SIMD に対するテザーの互換性とテザー数に応じて、2 要素幅、3 要素幅、4 要素幅のパックがランタイムに選択されます。12 個のテザーでは、1 (なし)、2 要素幅、3 要素幅、4 要素幅のパックを組み合わせることができます。
さまざまなスレッド数 (1:4 および 1:8) とさまざまなパック密度の PAOS (1 要素幅 (パックなし)、2 要素幅、3 要素幅、4 要素幅 double) を実行できるように、テザー数を 12 から 96 に増やした結果、パック (1、2、3、4) とスレッド数 (1、2、4、8) の任意の組み合わせが可能になりました。
追加のテザーは、ボディー (衛星) のシミュレーションに使用されるコードの非 PAOS 変更部分のロードを増やさないように、既存の衛星に接続されました。テザー数が大幅に増えるため、3、5、6、7 スレッドの理想的なテザー数は測定していません。
テストプログラムの構成は次のようになりました。
13 個のサテライトを 96 個のテザー (1 km) で接続
各テザーの構成: ~85 スカラー 57 個の次元 (3) の配列 3 個の次元 (3,3) の配列 22 個の次元 (3,~10000) の配列 52 個の次元 (~10000) の配列
96 * (85 + (57*3) + (3*3*3) + (22*3*1000) + (52*10000)) = 56,283,168 double (450MB)
テザー、衛星、惑星、その他をそれぞれ操作する変数も必要です。
ベースラインの参照シミュレーション時間に実行する適切な積分区間を決定するため、PAOS SIMD なしのシングルスレッド構成でテスト実行が行われました。シミュレーション時間区間ごとに、前のシミュレーション時間からのウォールクロック経過時間が表示されます。
テストはパック密度 (パックなし、2 要素幅、3 要素幅、4 要素幅) およびスレッド数 (1、2、3、4) の組み合わせに対して行われました。各構成は 4 つのレポート区間で実行され、最も小さな値を選択して比較しました。最も小さな値の選択は、システムでほかに実行されているプロセスの影響が最小限であるという仮定の下で行われました。
96 テザー、各 10,000 ビード - ターボオン、HT オフ
パックなし SIMD 2 要素幅 SIMD 3 要素幅 SIMD 4 要素幅 SIMD 1 202.461830544090 98.8166282926832 110.127472870544 96.2114920825516 2 113.080892757974 64.3881699061922 69.6634485553468 62.4252337711068 3 88.0928441275801 56.0872621388371 60.3187281050650 57.5615369606003 4 78.3640600375229 56.5572142589117 58.9836796998115 58.8164001500936
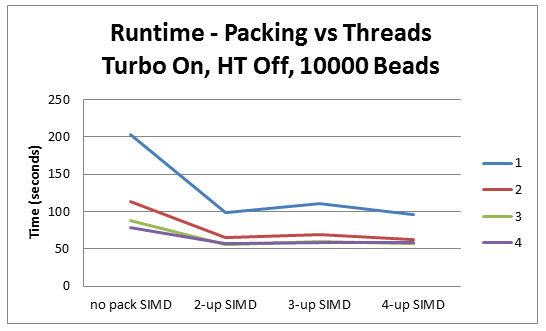
96 テザー、各 10,000 ビード - ターボオフ、HT オフ
パックなし SIMD 2 要素幅 SIMD 3 要素幅 SIMD 4 要素幅 SIMD 1 222.377931407129 108.414170956848 120.604551444653 105.015817485928 2 119.739932457786 67.4135627767355 73.9538575609758 65.4644253658544 3 90.9758964352723 56.9652196622883 61.5711771857414 58.8302754221386 4 80.8031147467163 57.1387076923083 59.7432093058160 59.3558339962474
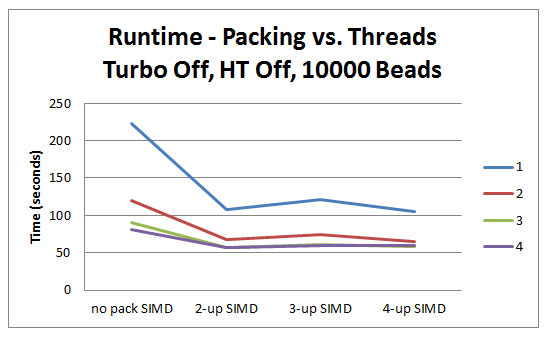
最初のテスト (1 スレッド、ターボオン、HT オフ) では、オリジナルのコードに対するスピードアップは 2.05 倍でした。3 要素幅のスピードアップは 1.88 倍で、4 要素幅のスピードアップは 2.10 倍でした。2 要素幅と 4 要素幅の差は 1.027 倍にすぎません。
2 スレッド以上では適切にスケーリングされていないように見えますが、このシミュレーションはメモリーを多用している (作業メモリー ~450MB) ことに注意してください。
3 要素幅のパフォーマンスを見てみましょう。テスト実行はビード数 4000 で行われました。
4000 ビード - ターボオン、HT オン
パックなし SIMD 2 要素幅 SIMD 3 要素幅 SIMD 4 要素幅 SIMD 1 91.3673146779801 50.2108811987264 53.7199640737510 47.4793344518262 2 55.4531537381101 34.9485817566820 35.3566061461863 31.8637723342063 3 45.6128820578588 31.2057180011579 30.7373190216704 28.4547075003547 4 45.9029787147183 30.9318707075290 30.1450711425587 29.1348981424198 5 45.9152253990896 30.9467731366030 30.1314135844295 29.2071261732417 6 52.4540275792824 36.6395676842658 34.7508676123107 33.7327393855012 7 55.0174089813809 39.3389245960061 36.7703592835023 36.2333221964363 8 60.0940263305092 42.1638867950896 39.0601884747230 39.5467420973800
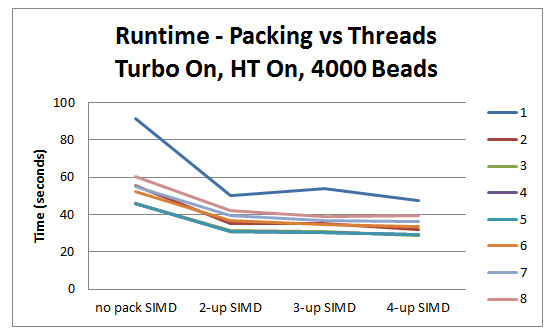
シングルスレッドのより少ないビード数では、パックなしと 2 要素幅のスピードアップが 2.05 倍から 1.82 倍に低下していることに注意してください。これは、非 PAOS コードと PAOS コードの比率が変化したためです。3 スレッドから 8 スレッドの実行では、3 要素幅よりも 2 要素幅のパフォーマンスが高く、8 スレッドでは、3 要素幅よりも 4 要素幅のパフォーマンスが高いことにも注意してください。今回の条件で実行したときに 4 要素幅が最適なのは明白ですが、プロセッサーの設計の違い、ビード数、テザー数によって結果は大きく変わります。最終レベルのキャッシュのサイズとデータセットのサイズの組み合わせによっては、3 要素幅が最適になる可能性もあります。
2 スレッド以上のスケーリングでスピードアップが低下するのは 3 つの要因によるものです。
a) データセットのフルサイズ (450MB) が L3 キャッシュよりも大きいため、アプリケーションがメモリー帯域幅の制限を受けます。これらのデータがすべてシミュレーション実行中に処理されるとは限らないことに注意する必要があります (中でも空気力学と電気力学のフォースは無効になります)。
b) インテル® Core™ i7 (Sandy Bridge) の AVX では、256 ビットのデータパスが利用できるとは限りません。一部の内部転送には 2 クロック必要です。より新しい Ivy Bridge プロセッサーでは、この問題は解消されます。
c) Sandy Bridge のデュアル・バンク・メモリーは、Ivy Bridge のクワッド・バンク・メモリーよりもメモリーバスの効率が低くなります。また、メモリーのノード数は 1 つです。2 プロセッサーの Ivy Bridge による NUMA 構成 (NUMA ノード 2 つ) では、クワッド・バンク・メモリーでそれぞれ、4 要素幅 SIMD 命令のパフォーマンスを効率的に実行できます。
まとめ
PAOS は、一部のアプリケーションでは非常に有効です。1P Sandy Bridge のシステムを 1P または 2P Ivy Bridge のシステムに変更すると、よりパフォーマンスが向上すると予想されます。さらに、メモリー帯域幅の制限がないアプリケーションで 4 要素幅の PAOS SIMD (AVX) を使用すると、よりパフォーマンスが向上することが予想されます。
PAOS は、サイズ要件が増加しますが、キャッシュラインの効率は良くなります (ヒット率が高くなります)。2 要素幅 SIMD はパックなしバージョンよりも作業ストレージのキャッシュ要件が 2 倍に、4 要素幅 SIMD は作業ストレージのキャッシュ要件が 4 倍になります。PAOS を使用する場合、ループ実行は減少するか分割されます。結果はワーキングセットのサイズやプロセッサーの世代に応じて異なります。
Copyright © 2012 Jim Dempsey. 無断での引用、転載を禁じます。
著者連絡先:
jim.00.dempsey@gmail.com http://www.linkedin.com/in/jim00dempsey
* その他の社名、製品名などは、一般に各社の表示、商標または登録商標です。
コンパイラーの最適化に関する詳細は、最適化に関する注意事項を参照してください。


