この記事は、https://www.oneapi.io/spec/ で 2023年9月14日に公開された『oneAPI 1.3 Provisional Specification Rev. 1』 (HTML、PDF) をベースにしています。原文は2000 ページ近くあり、翻訳の時間とリソースも限られるため、全文翻訳ではなく、記事形式で区切った仕様とその解説を提供することにしました。
この回では、『oneAPI 1.3 Provisional Specification Rev. 1』の「oneDAL」の「Decomposition」の節を取り上げています。
分解
主成分分析 (PCA)
主成分解析 (PCA) は、探索的データ解析と次元リダクション向けのアルゴリズムです。PCA は、1 セットの相関の可能性がある特徴の特徴ベクトル値を、主成分と呼ばれる相関しない特徴の新しいセットに変換します。主成分とは、分散が最大になる方向、つまりデータが最も分散する方向のことです。
| 操作 | 計算メソッド | プログラミング・インターフェイス | |||
|---|---|---|---|---|---|
| トレーニング | 共分散 | SVD | train(…) |
train_input |
train_result |
| 推論 | 共分散 | SVD | infer(…) |
infer_input |
infer_result |
数学的定式化
トレーニング
p 次元の特徴ベクトルのトレーニング・セット X = {x1, …, xn} と主成分の数 r であると考えると、問題はトレーニング・セット r 個の主方向 (p 次元固有ベクトル [Lang87] (英語)) を計算します。固有ベクトルは、各行に 1 つの固有ベクトルを含む r×p 行列 T にグループ化できます。
トレーニング法: 共分散
このメソッドでは、共分散行列の固有値分解によりデータセットの主成分を計算します。このメソッドは次の手順に従います。
- 共分散行列の計算
- 固有ベクトルと固有値の計算
- 結果を保存する行列の形成
共分散行列の計算は、次の方法で実行する必要があります。
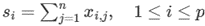合計ベクトル列を計算クロス積
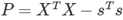を計算
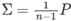共分散行列の計算
固有値 λi と固有ベクトル vi を計算するため、実装は [Ping14] (英語) など任意の方法を選択できます。
最後のステップは、ペアのセット (λi, vi) を λi の降順で並べ替え、結果として生成される行列 T=(vi,1, …, vi,1)、1 ≤ i ≤ p を生成します。さらに、初期データセットの平均と分散を返します。
トレーニング法: SVD
この方法では、データセットの特異値分解によってその主成分を計算します。この方法は次の手順によります。
- 特異値と特異ベクトルの計算
- 結果を格納する行列の形成
特異値 λi と特異ベクトル ui および vi を計算するため、実装は [Demmel90] (英語) など任意の方法を選択できます。
最後のステップは、ペアのセット (λi, vi) を λi の降順で並べ替え、結果として生成される行列 T=(vi,1, …, vi,r)、1 ≤ i ≤ p を生成します。さらに、初期データセットの平均と分散を返します。
サインフリップ法
一部の固有値ソルバーによって計算された固有ベクトルは、符号が曖昧であるため一意に定義されていません。決定論的な結果を得るには、サインフリップ法を適用する必要があります。[Bro07] (英語) で提案されるサインフリップ法の 1 つでは、行列 T を次のように変更する必要があります。
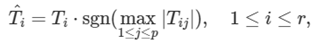
ここで、Ti は i 番目の行、Tij は j 番目と i 番目の列の要素、sgn(⋅) は符号関数です。
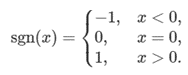
注: 上記のサインフリップ法は一例であり、oneDAL 仕様ではこのサインフリップ法の実装は必要ありません。実装する場合、固有ベクトルの符号を変更する任意の手法を選択できます。
推論
p 次元の特徴ベクトルの推論セット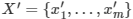 
とトレーニング・ステージで生成された r×p 行列 T を考慮すると、問題は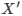 
をセット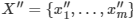 
に変換することです。ここで、
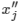は r 次元の特徴ベクトルです (1 ≤ j ≤ m)。
特徴ベクトル 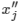は、行列 T によって定義された変換 [Lang87] (英語) を特徴ベクトル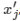 
に適用することで計算されます。
推論法: 共分散と SVD
共分散および SVD 推論メソッドは、(1) に従って 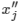を計算します。
使用例
使用例については、こちら (英語) を参照してください。
プログラミング・インターフェイス
この節のすべてのタイプと関数は、oneapi::dal::pca 名前空間で宣言され、oneapi/dal/algo/pca.hpp ヘッダーファイルをインクルードして使用できます。
プログラミング・インターフェイスについては、こちら (英語) を参照してください。
付録
k-d ツリー
k-d ツリーは空間分割二分木 [Bentley80] (英語) であり、
- それぞれの非リーフノードは特徴空間を 2 つの部分に分割する超平面を誘導します。分割超平面を明示的に定義するため、非リーフノードは特徴の識別子 (特徴空間の軸を定義) と、カットポイントを格納します。
- ツリーの各リーフノードには、トレーニング・データセット要素のサブセット (バケット) が関連付けられています。バケットから特徴ベクトルは、ルートノードからそれぞれのリーフへのパス上のツリーノードによって定義された空間の領域に属します。
関連する用語
カットポイント
k-d ツリーの非リーフノードに対応し、指定された特徴によって指定された軸に直交する分割超平面を定義する特徴値。
文献目録
文献目録については、こちら (英語) を参照してください。
法務上の注意書き
The content of this oneAPI Specification is licensed under the Creative Commons Attribution 4.0 International License (英語). Unless stated otherwise, the sample code examples in this document are released to you under the MIT license (英語).
This specification is a continuation of Intel’s decades-long history of working with standards groups and industry/academia initiatives such as The Khronos Group*, to create and define specifications in an open and fair process to achieve interoperability and interchangeability. oneAPI is intended to be an open specification and we encourage you to help us make it better. Your feedback is optional, but to enable Intel to incorporate any feedback you may provide to this specification, and to further upstream your feedback to other standards bodies, including The Khronos Group SYCL* specification, please submit your feedback under the terms and conditions below. Any contribution of your feedback to the oneAPI Specification does not prohibit you from also contributing your feedback directly to other standard bodies, including The Khronos Group under their respective submission policies.
By opening an issue, providing feedback, or otherwise contributing to the specification, you agree that Intel will be free to use, disclose, reproduce, modify, license, or otherwise distribute your feedback at its sole discretion without any obligations or restrictions of any kind, including without limitation, intellectual property rights or licensing obligations.
This document contains information on products, services and/or processes in development. All information provided here is subject to change without notice.
© Intel Corporation. Intel、インテル、Intel ロゴ、その他のインテルの名称やロゴは、Intel Corporation またはその子会社の商標です。
* その他の社名、製品名などは、一般に各社の表示、商標または登録商標です。
