この記事は、インテル® デベロッパー・ゾーンに掲載されている「Parallel Computation of Sparse Rulers」(http://software.intel.com/en-us/articles/parallel-computation-of-sparse-rulers) の日本語参考訳です。
この記事では、Sparse Ruler (まばらな定規) 問題の概要、この問題を計算する 2 つの並列コード、そしてこの問題のソリューションにとって興味深い「ギャップ」が明らかになったいくつかの新しい結果を紹介します。コードおよび結果は添付ファイルを参照してください。
概要
完全な Sparse Ruler は、M 個のマークで 0 から L ユニットまでのすべての整数距離を測定できます。例えば、次の定規には (最初と最後を含めて) 6 つのマークがあり、0 から 13 までの整数距離を測定できます。

この定規では、測定する距離に応じて、端ではなく途中のマークを使用します。例えば、8 ユニットは 2 と 10 のマークを使って測定します。詳細な説明と例については、Wikipedia の記事 (英語) を参照してください。Peter Luschny 氏の Web ページ (英語) の説明では、より少ないマークで同じ長さの完全な定規が存在しない場合を完璧 (perfect)、ほかに同じ数のマークでより長い完全な定規が存在しない場合を最適 (optimal) と呼んでいます。
最近の Al Zimmerman Programming Contest で出題された Graceful Graphs (http://azspcs.net/Contest/GracefulGraphs) は、Sparse Ruler に関連する問題でした。残念なことに、すでに知られていた Wichmann rulers (英語) により、このコンテストはつまらないものになりました。Wichmann の式を使用した上位 2 名の入賞者が、ありふれたソリューションであることを理由に受賞を断ったのです。しかし、Wichmann rulers が M>13 で最適であることは証明されているわけではなく、単に推測 (英語) されているに過ぎません。そのため、Wichman の式で推測されているものよりも長い完璧な Sparse Ruler を調査する価値があると判断しました。推測に対する反例は見つかりませんでしたが、この記事で後述している興味深い「ギャップ」が見つかりました。
これから紹介するプログラムは次の問題を解きます。
指定された L および M について、ソリューションが完璧な Sparse Ruler になると仮定し、完全な Sparse Ruler をすべて見つける。
この「完璧」という仮定により、余分なマークの追加方法を見つけるために時間を費やす必要はありません。プログラムは、見つかった定規と総数を出力します。完璧な Sparse Ruler の反転イメージは明白であるため出力しません。ただし、総数には含めます。Peter Luschny 氏は、既知の完璧な Sparse Ruler の数を表 (英語) にしています。
アルゴリズム
この問題のために 2 つのアルゴリズムを記述しました。どちらも再帰的な検索手法を使用していますが、距離のセットの表現が異なります。はじめにアルゴリズムの同一部分を説明した後、詳細について述べます。重要な再帰ルーチンは、定規の両端から中心に向かって進むことから、「Scrunch」という名前にしました。引数は次の 4 つです。
- 一部マークされた定規
- avail – 定規に追加できる残りのマーク数
- w – すでにマークされている両端の領域の幅
- uncovered – 一部マークされた定規で測定できていない距離のセット
例えば、M=8 で L=23 の定規を考えてみましょう。次の図は、検索の際に Scrunch に渡される引数を示しています。赤は、残りのマーク数 avail を追加できる位置です。

このシナリオで、Scrunch ルーチンは次の 4 つの可能性を考慮します。
- 位置 5 にマークを追加します。
- 位置 18 にマークを追加します。
- 両方の位置にマークを追加します。
- 両方の位置にマークを追加しません。
次に、緑の領域を 1 ユニット拡大し、新しい定規を再帰的に検索します。検索は次の 4 つのいずれかの理由により停止します。
- 完全な Sparse Ruler が見つかった。
- avail 個のマークを追加して生成可能な距離の数よりも多くの距離の数が uncovered に含まれている。avail 個のマークを追加して生成できる距離の数は、それらのマーク間に avail*(avail-1)/2 個、およびそれらのマークと既存のマーク間に avail*(M–avail) 個です。
- avail 個のマークを追加できるスペースが残っていない。
- 白い領域に別のマークを追加してもカバーできない長さの距離が uncovered に含まれている。ほとんどの部分で、新しい距離は新しいマークから定規の両端のいずれかまでの距離になるため、新しいマークで作成される最も長い距離 d は d<L–w に制限されます。
2 つ目と 3 つ目の理由は鳩の巣原理の実例です。
最上位の Scrunch への呼び出しは、両端のみマークされた定規、つまり、avail=M-2、w=0、uncovered = {1..L-1} になります。Scrunch ルーチンの動作は次のようになります。
Scrunch( avail, w, ruler, uncovered ) {
u = セット uncovered の距離の数
If u > 0 then
If u > avail*(avail-1)/2+avail*(M-avail) then
return // カバーする数が多すぎる
While (avail 個のマークを追加できるスペースが残っている) do
w = w+1
Try (位置 w および / または L-w にマークを追加し、各ケースについて Scrunch を再帰的に呼び出す)
If (距離 L-w をカバーできない)
return // カバーできない長い距離がある
Else
(完全な Sparse Ruler を出力)
}
Try 部分では、前述の 4 つの可能性のうち 3 つを確認します。4 つ目の可能性 (マークを追加しない) の確認はループバックにより行われます。このループは 4 つ目の可能性のために手動で最適化された末尾再帰であり、完全な再帰バージョンでは再確認するループ不変条件を再確認しません。
鳩の巣原理による検索の停止はアルゴリズムを高速化できます。また、いくつかの定数係数の向上もメリットがあります。まず、スケッチには含まれていませんが、対称ソリューションのための余分な作業を行っていません。実際のコードは、定規の反転イメージを検索していません。
次に、このアルゴリズムは並列実行に適しています。サブ検索はそれぞれ独立しているため、並列に処理できます。while ループは検索の完了を待つ必要がないため、検索が行われている間も自由にループを続行できます。理想的な並列ハードウェアでは、並列化により漸近のスピードアップが可能になり、実行時間はクリティカル・パスの長さまで短縮されます。実際には、並列ハードウェアは有限であるため、並列化により定数係数が向上します。しかし、後述するように、ここでは大規模なハードウェア (つまり大きな定数) へアクセスしていました。
3 つ目に、再帰呼び出しでは新しい uncovered の計算に最も時間がかかるため、セット uncovered の演算を速くする必要があります。次の 2 つの節で、uncovered を表現する 2 つの方法を説明します。
定規のビットマスク表現
Tomas Sirgedas 氏は、コンテスト・ディスカッション・グループでこのアプローチを最初に説明しました。重要な点は、定規を 2 つの半分の定規として表現したことです。半分の定規はそれぞれ、ビットマスクとして表現されました。セット uncovered もビットマスクとして表現され、「カウント」命令を用いてサイズを取得します。Tomas 氏が優れていたのは、ビット位置が両端から中心に向けて計算されるように、半分の定規のマスクの 1 つを反転したことです。反転により、ビット単位演算を使用して uncovered を迅速に更新できるようになりました。定規の半分のマスクで、ビット k は端から k ユニット内側のマークに相当します。コードでは、反転した半分を near、残りの半分を far と呼んでいます。マークを一時的に配置するとき、そのマークが配置される半分は near、残りの半分は far になります。
uncovered のマスク表現は L+1 ビットから成り、2 つのサブマスク lo および hi 間で分割されます。
- lo は半開区間 [0,ceil(L/2)) の距離を保持します。ビット k は距離 floor(L/2)-k に相当します。
- hi は閉区間 [ceil(L/2),L] の距離を保持します。ビット k は距離 L–k に相当します。
定規の半分 near と far、および位置 w の新しいマークを指定することにより、セット uncovered をシフト演算とビット単位演算を使用して更新できます。
lo &= ~(near << (L/2-w)) lo &= ~(far >> (L-L/2-w)) hi &= ~(far << w)
次の図はビットの対応例を示しています。各ビットマスクは色付きで示されます。右端のマスクは暗黙でビット 0 となり、ビットの位置は左向きに昇順になっています。定規上の数値はマークの位置を示します。定規の半分 near は反転して表示されています。{0,1,4,17,21,23} にマークされているこの定規で、6 (赤) にマークが追加されました。赤の線は、定規の半分のマスクをシフトすることにより、位置 6 にマークすることで新しい距離がどのように計算されるか示しています。例えば、位置 21 のマークは位置 6 の新しいマークから距離 15 にあるため、uncovered の対応するビットをクリアする必要があります。
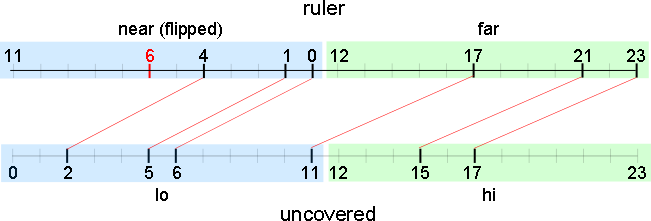
定規の半分の長さで最初に左にシフトされているため、lo に対する far の影響はコードでは右シフトになります。uncovered を分割するポイントは、更新を単純にするために選択されました。near 部分は hi に影響しません。
定規の半分を反転する別のメリットは、対称テストが簡単になり、余分な作業を回避できることです。
bitscrunch.cpp ファイルには、重要な計算の 2 つの実装が含まれています。どちらの実装も、組込み関数 _mm_popcnt_u64 を用いてセット uncovered のサイズを計算しています。実装の違いは次のとおりです。
- 1 つはシフト演算とビット単位演算に標準の C++ 演算を使用しているため、定規の半分の長さが
size_tのビット数に制限されます。 - もう一方は、SSE を使って 128 ビット演算を行っているため、L=255 まで演算できます。
デフォルトでは SSE バージョンが有効になっています。別のバージョンを使用するには、ソースの #if 0 を #if 1 に変更します。
漸近的にはより速いが実際にはより遅いアプローチ
完璧な Sparse Ruler では、L は M の 2 乗であるため、ビットマスク・アプローチは uncovered の重要な演算に O(M2) 倍かかります。コンテストでは M=97 までの問題が含まれていたため、当初ビットマスク・アプローチの採用は考えていませんでした。最初のアルゴリズム ( scrunch.cpp ファイルを参照) では、バイト配列を使用して uncovered を表現していました。各要素 uncovered[k] は、要素 k が存在する場合は 1、存在しない場合は 0 でした。マークを追加するとき、配列は新しいマスクで作成された O(M) の新しい距離について O(M) 回更新され、セットのサイズは段階的に増加します。コンテストの目的が「Wichmann に勝つこと」になった途端、M の最大値が 25 程度であることが明らかになり、定数係数の利点が活かされることになりました。しかし、ビットマスク・アルゴリズムの制限を超える L の問題には、ワードサイズによる制限がない最初のアルゴリズムを使用しました。これらの問題では、M が L に対して小さすぎるため解が存在しないという結果を、検索を高速に実行して得ることができました。
scrunch.cpp の再帰手法 scrunch は、はじめに説明したものと本質的に同じですが、再帰レベルを一度に 1 つの緑ゾーン分だけ拡張して左右を交換するため、より困難です。
並列化
コードは、再帰の並列化に優れたインテル® Cilk™ Plus で並列化されています。再帰呼び出しは cilk_spawn を使用してスポーンされています。並列スケジューリングのオーバーヘッドのほうが大きくなる場合 (avail<Cutoff の場合) はシリアル再帰を使用します。次のやや簡略化された bitscrunch.cpp のコードは重要なロジックを示しています。マクロ SCRUNCH はカットオフロジックを処理します。
template<typename T>
T Clone( const T& x ) {return x;}
#define SCRUNCH(a,w,l,r,u) do {
if( (a)>=Cutoff ) cilk_spawn Scrunch(a,w,Clone(l),Clone(r),Clone(u));
else Scrunch(a,w,l,r,u);
} while(0)
static void Scrunch( int avail, int w, const HalfRuler& left, const HalfRuler& right, const UncoveredSet& uncovered ) {
if( auto u = uncovered.count() ){
if( u > MaxUnique[avail] )
return; // カバーする数が多すぎる
while( 2*w < L-avail ) {
++w;
UncoveredSet ul(uncovered);
// 左半分の w のマークでカバーされた距離を削除
ul.strike( left, right, w );
UncoveredSet ur(uncovered);
// 右半分の w のマークでカバーされた距離を削除
ur.strike( right, left, w );
HalfRuler lw(left,w); // w のマークを含む左半分
HalfRuler rw(right,w); // w のマークを含む右半分
if( 2*w!=L ) {
SCRUNCH( avail-1, w, lw, right, ul ); // 左で w を試す
if( left!=right )
SCRUNCH( avail-1, w, left, rw, ur ); // 右で w を試す
if( avail>=2 ) {
UncoveredSet ub(ul&ur); // 左右で w を試す
ub.remove(L-2*w);
SCRUNCH( avail-2, w, lw, rw, ub );
}
} else {
Scrunch( avail-1, w, lw, rw, ul&ur ); // w は中心点
break;
}
if( uncovered.hasFar(w) )
break; // カバーできない長い距離がある
}
} else {
TallyRuler(avail, left, right); // 完全な Sparse Ruler が見つかった
}
}
関数テンプレート Clone はいくつかの存続期間の問題を解決します。関数がスポーンされると、スポーンされた関数がリターンするまで、その呼び出しに関連する、コンパイラーにより生成された一時オブジェクトは存続します。ただし、いくつかの引数は、while ループの本体により存続期間が制限されるローカル変数への参照です。while ループはスポーンされた呼び出しの実行中も処理を続行できるため、そのローカル変数を関数 Clone でコピーする必要があります。代案はすべての引数を値で Scrunch に渡すことでしたが、この方法はわずかに遅いことがテストで分かりました。
インテル® Cilk™ Plus は非常に厳密であり、スポーンされた関数がすべて完了するまで関数はリターンできないため、マクロ SCRUNCH はインライン関数ではなくマクロでなければいけません。代案は、言語 X10 のように、スポーンされた関数が実行していても関数がリターンできる部分的に厳密なセマンティクスです。完全に厳密なセマンティクスはプログラムに対する推測を容易にし、インテル® Cilk™ Plus の実装を単純化しますが、ここでは部分的に厳密なセマンティクスのほうが便利でした。
while ループにおける同期の欠如により、インテル® Cilk™ Plus の「継続-スチール」セマンティクスを使ってメモリー消費を制限することが不可欠でした。インテル® TBB や OpenMP* の「タイドなタスク」のような「子-スチール」システムでは、アイドル・ワーカー・スレッドがスポーンされたタスクをスチールするため、現在のスレッドがループを実行して完了します。残りのワーカーがビジーの場合は常に、実行する前に多くのタスクが溜まってしまいます。インテル® Cilk™ Plus のような「継続-スチール」システムでは、現在のスレッドはスポーンされたタスクに直ちに移動し、アイドルワーカーによってスチールされる呼び出し元の継続は残されます。そのため、while ループは自身で停止し、アイドルワーカーが利用可能になったときのみ先に進みます。
決定性
プログラムは、ロックがないにもかかわらず、インテル® Cilk™ Plus のレデューサー (https://www.cilkplus.org/tutorial-cilk-plus-reducers) を用いることで決定論的です。各レデューサーは複数のビューを提供します。実行の各並列ストランドは異なるビューを参照するため、各ストランドはほかのストランドに影響されることなくビューを更新できます。インテル® Cilk™ Plus のランタイムは自動で適切にビューをマージします。
次に 2 つのレデューサーの宣言を示します。
// 見つかった定規の数。非対称の定規は 2 回カウントされる。 static cilk::reducer_opadd<int> Count; // 出力ストリーム static cilk::reducer_ostream Out(std::cout);
各レデューサーは「ビューのポインター」のように動作します。次に Count および Out を更新する TallyRuler のコードを示します。
// Sparse Ruler のソリューションを出力。
void TallyRuler( int avail, HalfRuler left, HalfRuler right ) {
*Out << "Ruler[" << M-avail << "]:";
// ソートされた順にマークを出力。アルゴリズムは 2 乗だが、
// マークの計算に費やされる大幅な労力と比べると必要な労力は少ない。
for( Mark i=0; i<=L; ++i )
if( i<=HalfL && left[i] || RestL<=i && right[L-i] )
*Out << " " << unsigned(i);
*Out << std::endl;
*Count += 1 + (left!=right);
}
連想性によりランタイムに更新とビューのマージが再結合されるため、レデューサーは任意の結合操作で動作します。出力が部分的にバッファーされるため Output ストリームの操作は結合操作であり、バッファーの連結は結合操作です。詳細な理論については、「Reducers and Other Cilk++ Hyperobjects」 (英語) を参照してください。
スケーリング
大きな定規問題でも、コードは優れたスケーリングを示しました。
- ハードウェアで可能な並列性よりもはるかに多くの並列性が利用できます (「並列スラック」)。スラックにより、インテル® Cilk™ Plus のワークスチール・スケジューラーはロードバランスを自動的に保ちます。
- ワーキングセットは小さいため、メモリー帯域幅はリソース・ボトルネックになりません。
スケーリングの測定について簡単に説明します。P のワーカー (ハードウェア・スレッド) で実行しているプログラムの実行時間は TP で表されます。シリアル実行時間は T1、スピードアップは T1/TP です。T1 が 1 つのワーカーで実行している並列プログラムの場合は相対スピードアップと呼ばれます。T1 が最も一般的なシーケンシャル・プログラムの時間の場合は絶対スピードアップと呼ばれ、並列オーバーヘッドを考慮したり、並列可能なアルゴリズムに限定する必要はありません。並列プログラムの効率 は、スピードアップを P で割って求めます。使用するスピードアップに応じて、相対または絶対として表されます。絶対効率 1.0 は理想値で、達成するのは困難です。
ここでは、プログラムを 256 コアの SGI UV Altix 1000 で実行しました。各コアのハードウェア・スレッドは 1 つです。次のグラフは、そのマシンで M=21 および L=153 にした場合の bitscrunch の効率を示しています。
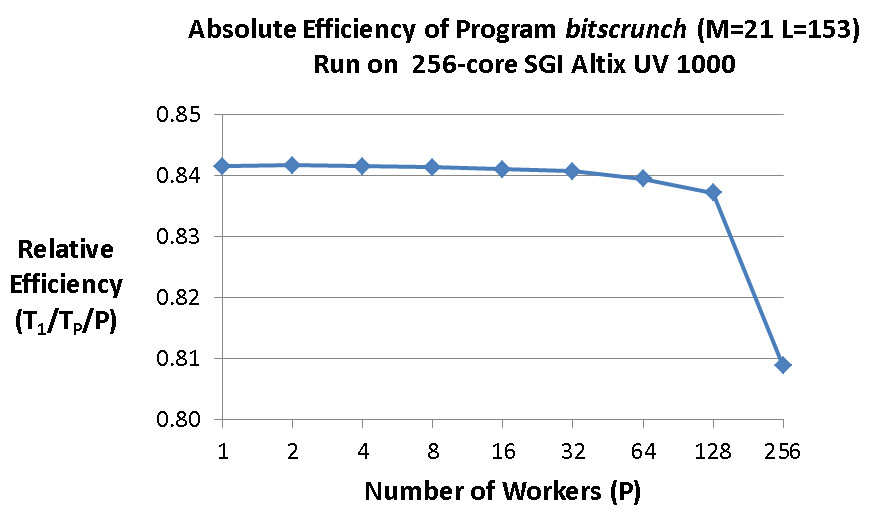
グラフは、256 ワーカーにスケールした場合でもプログラムの絶対効率が理想値のほぼ 0.8 倍になることを示しています。縦軸は省略されていることに注意してください。右下がりになっている部分は実際には非常にわずかです。相対効率は最適な相対スケーリングの 4% に収まっています。
最も時間がかかったのは M=25 および L=208 の場合で、256 コアを使用して約 51 時間でした。
インライン展開
多くのプログラマーは C++ のインライン機能を使いすぎる傾向にあります。例えば、クラスの内部でメンバー関数を (宣言しないで) 定義することは便利ですが、その結果これらの関数は暗黙的にインラインとしてマークされます。多くのインライン展開を行うと、命令キャッシュミスが増え、パフォーマンスが低下します。このため、最近のコンパイラーは、インライン展開に対するプログラマーの要求を考慮するヒューリスティックを採用していますが、常に要求に従うとは限りません。インテル® VTune™ Amplifier で初期のバージョンをプロファイルすると、インライン展開したかったいくつかの重要なルーチンが icc でインライン展開されていませんでした。そのため、インライン展開したい場所に #pragma forceinline を指定しました。同様に、icc がインライン展開を行うように、メソッド UncoveredSet::count に明示的な inline キーワードを (余分に) 指定しています。
定規の結果 -- 興味深いギャップ
添付の zip ファイルには、結果の表 SparseRulerCounts.pdf (M=25 までの結果) が含まれています。「Count」は指定された M および L で見つかった定規の数です。ほとんどの結果は bitscrunch.cpp で生成されました (L>=250 の結果は scrunch.cpp で生成)。
表から、Wichmann の式は 13<M<=25 の最適な定規のみ生成することが確認できます。
新しい発見は、M と L では完璧な定規が生成できるのに、M と L-1 では生成できないというギャップの存在です。例えば、表の一部を次に示します。
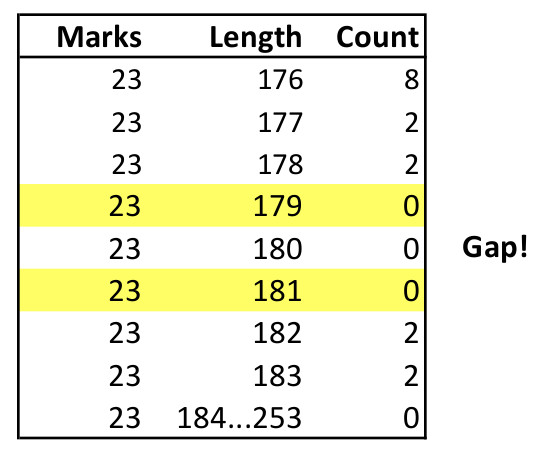
黄色の行は Tomas Sirgedas 氏が記述したプログラムで検証されていた部分です (この検証は 256 コアではなく 4 コアで行われものです; 氏の忍耐に敬意を表します)。ギャップが存在する場合、定規の数が増えるとともに、その数も多くなると考えられます。Wichmann の式と「オフ・バイ・ワン」の変形は、ほかのソリューションより優れているだけでなく、問題サイズが大きくなればなるほどほかのソリューションよりも有利になることが分かります。
謝辞
ビットマスクの反転のヒントを提供し、いくつかのギャップを検証してくれた Tomas Sirgedas 氏に感謝します。Tomas Sirgedas 氏および Neal Faiman 氏は、この記事の草稿をレビューしてくれました。また、256 コアの SGI UV Altix システムを週末に利用させてくれた並列ランタイムチームに感謝します。時間のかかる検証を行えたのはチームのおかげです。
インテル® Cilk™ Plus の詳細は、https://www.cilkplus.org/ (英語) を参照してください。
| 添付ファイル | サイズ |
|---|---|
| sparse-ruler.zip http://software.intel.com/sites/default/files/managed/2a/59/sparse-ruler.zip |
46.64KB |
コンパイラーの最適化に関する詳細は、最適化に関する注意事項を参照してください。


