並列性 (パラレリズム) は決定論に影響するか?

この記事は、Dr.Dobb’s に掲載されている「Does Parallelism Affect Determinism?」 (http://drdobbs.com/go-parallel/blog/archives/2010/06/does_parallelis.html) の日本語参考訳です。

2 つのスレッドを使用して、それぞれ別のコアで、同じコードを同じ入力で同時に実行した結果が異なる場合、このコードは非決定論的であるといえるだろうか?

最近、私たちは、自身のプログラムをそのように表現した同僚と話し合う機会がありました。この状況で「非決定論的」という言葉を使うことは、私たちにはやや奇妙に思えました。

そもそも、「決定論」と「非決定論」とは何を意味するのでしょうか? NIST (アメリカ国立標準技術研究所) によれば、「決定論的アルゴリズム」とは「その動作を入力から完全に予測することができるアルゴリズム」と定義されています。さらに「…入力セットが同じ場合は、常にアルゴリズムは同じ計算を実行し、同じ結果を返す」と明記されています。

当然、これは私たちが望むことであり、その同僚が望んでいたことであり、すべてのプログラマーが望むことでもあります。そして、その唯一の答えが正解であり、答えはその一つしかないのです。その答えには機能的な正しさがあります。私たちは、あるときは 2、またあるときは 4 というように、1 + 1 に対して異なる結果を生成するプログラムは必要としていません。

非決定論的アルゴリズムはどうでしょうか?

ある時点で 2 つ以上のステップを含み、常に正しいステップまたは最適なステップを取る概念的なアルゴリズムです。

入力セットから 2 つ以上のステップがあること以外に、非決定論的アルゴリズムの特徴は、許容可能な出力結果が 2 つ以上あること、または許容可能な 1 つの出力結果に到達するパスが複数あることです。

このアルゴリズムは有限状態機械 (FSM) として表すことができます。どのような問題であっても有限状態機械として表すことが可能で、1 つまたは複数の解決法はその機械を通るパスとして表します。

図 1(a): 決定論的な有限状態機械（DFSM）

図 1(b): 非決定論的な有限状態機械 (NFSM)

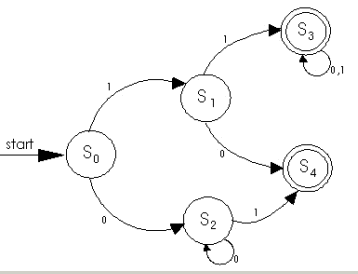
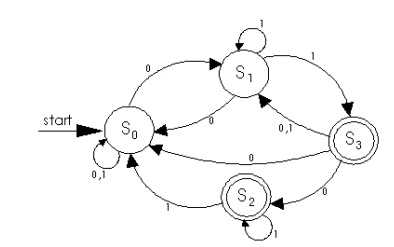
図 1(a) は決定論的な有限状態機械 (DFSM)、図1 (b) は非決定論的な有限状態機械 (NFSM) を表したものです。これらは次のように定義されます。

FSM = (S,I,f,s_o,F)

ここでは

S は状態の有限セットです。
I は入力の有限セットです (この場合は 1 と 0)。
s_o は 1 つの初期状態または初期状態のセットです。
F は最終の (許容された) 状態を表す S のサブセットです。
f は遷移関数です。

この 2 つの有限状態機械の違いは、初期状態 (非決定論では初期状態が複数になることがある) と遷移関数です。f_d (決定論的な遷移関数) は個々の入力と状態の組み合わせに対して 1 つの状態を割り当て、f_n (非決定論的な遷移関数) は個々の入力と状態の組み合わせに対して状態のセットを割り当てることができます。表 1 は、それぞれの有限状態機械における状態遷移の比較表です。

表 1:DFSM と NFSM の状態遷移の比較表

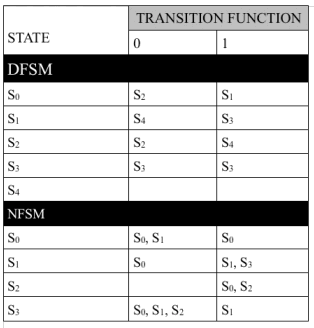
最終の (または許容された) 状態は、入力だけでなく、現時点の状態により決定されます。

問題によっては、本質的に決定論的か、非決定論的か分類できるものもあります。当然、数学的な関数はすべて決定論的です。一方、飛行機のチケットを予約する場合、出発地と最終目的地を結ぶルートは複数あることが考えられます。定義上、NP 完全問題は多項式時間で解決できない非決定論的な問題です。ゲームが決定論的であるならば、それはとても退屈なものになってしまうでしょう。勝つまでにあらゆるパスがあるからこそ、ゲームをプレイしたいと思うわけです。

非決定論は、ゲームを何度もプレイしたいという価値を決定します。今、私たちは『侍道 3』、『龍が如く 3』、『フォールアウト 3』をプレイしています。これらのゲームは非決定論の究極的な応用といえるでしょう。これらのゲームでは、同じキャラクターを使ってさまざまなパスをプレイできますが、結果の数は限られています。『フォールアウト 3』で主人公がメガトンの街を爆破する方法が何通りあるのかをここで言うことは野暮というものです。それこそが、ゲームを何度もプレイしたいという価値だからです。

一方で、判断が難しい問題もあります。乱数ジェネレーターを使用するアルゴリズムでは、入力は同じでも出力を予測することは困難です。そのようなアルゴリズムでは、状態がランダムに変化し、異なる結果が導かれます。これは決定論的と見なすべきでしょうか? それとも非決定論的と見なすべきでしょうか? 非決定論的アルゴリズムは決定論的アルゴリズムに変換することもできます。

ここで、最初に触れた、私たちと同僚の奇妙なコードについてのディスカッションに戻りましょう。

2 つのスレッドを使用して、それぞれ別のコアで、同じコードを同じ入力で同時に実行した結果が異なる場合、このコードは非決定論的であるといえるでしょうか?

このコードでは、シーケンシャルに実行した場合と、シングルコア・マシンでスレッドを追加した場合には期待通りの結果が得られました。しかし、マルチコアマシンで実行した場合には、結果が不安定になりました。

決定論的なコードが魔法のように非決定論的なコードに変わってしまったのでしょうか? そうではなく、このプログラムにはもともと不安定な結果をもたらす何らかの潜在的な問題があったと考えられます。それが、マルチコアでコードを実行し出力に影響が現れるまで明らかにならなかったのでしょう。

ここでは、外的要因 (おそらく別のスレッド) により、コードで共有されている値が予期せず変更されてしまった可能性があります。シングルコア・マシンで複数のスレッドで実行したときには (たまたまタイミングのために) この予期しない変更は起こらなかったものの、マルチコアマシンで各スレッドを個別のコアで実行したときには変更されてしまったのでしょう。

コードをマルチコアで実行する場合、タイミングによってその他の問題が発生することもあります。プロセッサーの速度が速いかまたは遅いかによって、予期せずに値がメモリーに書き込まれたり、または書き込まれなかったりします。入出力デバイスの速度やグローバル変数にも注意が必要です。このような各種の問題のため、決定論的な有限状態機械は追加の状態が必要になり、その結果、アルゴリズムの新しいパスにより決定論的なコードが非決定論的なコードに変換されてしまうことがあります。