この記事は、インテル® デベロッパー・ゾーンに掲載されている「Accelerating Compute-Intensive Workloads with Intel® Advanced Vector Extensions 512 (Intel® AVX-512) Using Microsoft Visual Studio*」(https://software.intel.com/en-us/articles/accelerating-compute-intensive-workloads-with-intel-avx-512-using-microsoft-visual-studio) の日本語参考訳です。
概要
昨年、私たちは、VC++ blog (英語) で Microsoft* Visual Studio* 2017 でのインテル® アドバンスト・ベクトル・エクステンション 512 (インテル® AVX-512) のサポートについて紹介しました。この記事の補足として、インテル® AVX-512 がパフォーマンス上の利点をどのようにもたらすのか、いくつかの例を示して説明します。ここでは、配列の平均値計算、行列ベクトルの乗算、およびマンデルブロ集合の計算の例を使用します。これらの例をビルドするには、Microsoft* Visual Studio* 2017 バージョン 15.5 以降 (最新バージョンを推奨)、およびそれらを実行するにはインテル® AVX-512 命令セットをサポートするインテル® プロセッサーを搭載したコンピューターが必要です。プロセッサーの情報については、ARK ウェブサイトをご覧ください。
テストシステムの構成
これらの例のコンパイルと実行に使用したハードウェアとソフトウェアの構成は次のとおりです。
- プロセッサー: インテル® Core™ i9-7980XE エクストリーム・エディション・プロセッサー @ 2.60GHz、18 コア/36 スレッド
- メモリー: 64GB
- OS: Windows® 10 Enterprise バージョン 10.0.17134.112
- Windows* の電源オプション: バランス
- Microsoft* Visual Studio* 2017 バージョン 15.8.3
注: 最新のプロセッサーのパフォーマンスは、メモリーとストレージの容量と種類、グラフィックスとディスプレイ・システム、プロセッサーの構成、およびプログラムがそれらをどの程度効率良く利用するかなど、多くの要因に依存します。そのため、ここで示す結果は、ほかの構成における結果と完全に一致しない可能性があります。
サンプルの概要: 配列の平均値計算
インテル® AVX-512 組込み関数を使用してコードを記述する簡単な例を見てみます。インテル® アドバンスト・ベクトル・エクステンション (インテル® AVX) とインテル® AVX-512 命令は、同じデータ型の複数の要素を含む計算ベクトルを使用して、計算を強化するように設計されています。これらのインテル® AVX とインテル® AVX-512 組込み関数を使用して、浮動小数点配列の平均計算を高速化します。
まず、スカラー (非ベクトル) 計算により配列 a の平均を求める関数から始めます。
1 2 3 4 5 6 7 8 9 | static const int length = 1024*8;static float a[length];float scalarAverage() { float sum = 0.0; for (uint32_t j = 0; j < _countof(a); ++j) { sum += a[j]; } return sum / _countof(a);} |
この関数は、配列のすべての要素を合計して、要素数で除算します。この計算をベクトル化するには、配列を要素のグループ、つまり同時に計算できる「ベクトル」に分割します。インテル® AVX の場合、それぞれの浮動小数点要素は 32 ビットで、ベクトル長は 256 ビットであるため、各ベクトルには 8 個の浮動小数点要素を格納することができます。つまり、256/32 = 8 の浮動小数点要素になります。すべてのグループの合計は、部分ベクトルを合計にしてから、そのベクトルの要素を加算して最終的な合計を求めます。簡略化のため、以下に示すサンプルコードでは、要素数はインテル® AVX では 8 の倍数、インテル® AVX-512 では 16 の倍数であると仮定します。合計要素数がこのベクトルに収まらない場合、残りを処理するためリマインダー処理を記述する必要があります。
以下に新しい関数を示します。
1 2 3 4 5 6 7 8 9 10 11 | float avxAverage () { __m256 sumx8 = _mm256_setzero_ps(); for (uint32_t j = 0; j < _countof(a); j = j + 8) { sumx8 = _mm256_add_ps(sumx8, _mm256_loadu_ps(&(a[j]))); } float sum = sumx8.m256_f32[0] + sumx8.m256_f32[1] + sumx8.m256_f32[2] + sumx8.m256_f32[3] + sumx8.m256_f32[4] + sumx8.m256_f32[5] + sumx8.m256_f32[6] + sumx8.m256_f32[7]; return sum / _countof(a);} |
ここで、_mm256_setzero_ps (英語) は、sumx8 に割り当てられる 8 つのゼロ値のベクトルを生成します。次に、配列から 8 つの連続した要素セットを _mm256_loadu_ps (英語) で 256 ビットのベクトルにロードして、_mm256_add_ps (英語) で sumx8 の対応する要素に加算し、sumx8 を 8 つのベクトルの小計にします。最後に、それらの小計から合計を求めるため加算します。
スカラー実装と比較すると、単一命令複数データ (SIMD) 実装ではより少ない加算命令を実行します。n 個の要素を持つ配列では、スカラー実装は n 個の加算命令を実行しますが、インテル® AVX を使用すると (n / 8 + 7) 個の加算命令のみが実行されます。その結果、インテル® AVX 実装では、スカラー実装よりも最大 8 倍高速化される可能性があります。
同様に、インテル® AVX-512 バージョンを示します。
1 2 3 4 5 6 7 8 | float avx512AverageKernel() { __m512 sumx16 = _mm512_setzero_ps(); for (uint32_t j = 0; j < _countof(a); j = j + 16) { sumx16 = _mm512_add_ps(sumx16, _mm512_loadu_ps(&(a[j]))); } float sum = _mm512_reduce_add_ps (sumx16); return sum / _countof(a);} |
このバージョンは最終的に合計を計算する方法を除き、前の関数とほぼ同一です。ベクトルに 16 個の要素がある場合、インテル® AVX バージョンと同じ方法で最終的な合計を求めるには、16 回の配列参照と 15 個の加算が必要になります。幸いなことに、インテル® AVX-512 では _mm512_reduce_add_ps (英語) 組込み関数を使用して同じ結果を生成できます (コードの可読性が高まります)。この関数は、4 つの加算命令だけで、最初の 8 つの要素を残りの部分に加算し、次に残りの部分にそのベクトルの最初の 4 つを加算し、次に 2 つを加算して、最終的にそれらを合計します。インテル® AVX-512 命令を使用して n 個の要素の配列の平均を求める際に n が十分に大きい場合、インテル® AVX の半分の加算命令 (n / 16 + 4) で計算を実行できます。その結果、インテル® AVX-512 実装では、インテル® AVX 実装よりも最大 2 倍高速化される可能性があります。
この例では、インテル® AVX-512 の最も基本的な組込み関数を使用しましたが、インテル® AVX-512 には 128 ビット、256 ビット、および 512 ビット・ベクトルのさまざまなデータ型に対し各種演算を実行し、マスクや丸めを提供する数百のベクトル組込み関数があります。これらの関数は、インテル® AVX-512 を含むインテルの各種命令セット拡張を使用することがあります。例えば、_mm512_add_ps() (英語) 組込み関数は、インテル® AVX-512 の vaddps 命令を使用して実装されます。インテル® AVX-512 の詳細については、『インテル® ソフトウェア開発者マニュアル』 (英語) を、特定の組込み関数の詳細を知るには、『インテル組込み関数 (イントリンジックス) ガイド』 (英語) をご覧ください。『インテル組込み関数ガイド』 (英語) の関数エントリーをクリックすると、概要、説明、操作などの詳細が表示されます。
これらの関数は、immintrin.h ヘッダーファイルで宣言されています。Microsoft* もまた、immintrin.h からの抜粋を含む、ほぼすべての Microsoft* Visual C++* (MSVC) 組込み関数を定義する intrin.h ヘッダーを提供しています。ソースファイルでは、これらのヘッダーのいずれかをインクルードできます。
サンプルの概要: 行列ベクトル乗算
数学的なベクトルと行列演算には、多くの乗算と加算が含まれます。例えば、以下は簡単な行列とベクトルの乗算です。
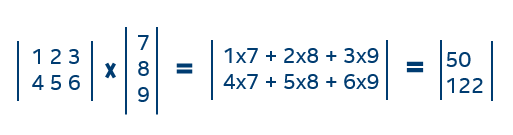
プロセッサーはこの簡単な計算を瞬時に実行できますが、大規模なベクトルと行列を乗算する場合、数百から数千の乗算と加算を行う必要があります。それらの計算を高速化するため、どのように「ベクトル化」できるか見てみましょう。行列 t1 と t2 を乗算するスカラー関数をご覧ください。
1 2 3 4 5 6 7 8 9 10 11 12 | static float *out;static const int row = 16;static const int col = 4096;static float *scalarMultiply() { for (uint64_t i = 0; i < row; i++) { float sum = 0; for (uint64_t j = 0; j < col; j++) sum = sum + t1[i*col + j] * t2[j]; out[i] = sum; } return out;} |
前述の例と同様に、各行をベクトルに分割して計算のベクトル化を試みます。インテル® AVX-512 では、ベクトル幅は 512 ビットであるため、ベクトルは 512/32 = 16 個の単精度浮動小数点要素を格納できます。これは計算ベクトルであり、乗算される数学ベクトルとは異なることに注意してください。行列の各行から、16 個の列と対応する 16 個のベクトル要素をロードし、それらを乗算して、その積を 16 要素のアキュムレーターに格納します。行の計算を完了したら、アキュムレーターの要素を合計して結果要素を取得できます。
注: インテル® AVX やインテル® ストリーミング SIMD 拡張命令 (インテル® SSE) でも同様のことが可能であり、それぞれの拡張のベクトル幅は 8 (256/32) および 4 (128/32) 要素です。
以下に、インテル® AVX-512 組込み関数を使用した乗算関数を示します。
1 2 3 4 5 6 7 8 9 10 11 12 13 | static float *outx16;static float *avx512Multiply() { for (uint64_t i = 0; i < row; i++) { __m512 sumx16 = _mm512_set1_ps(0.0); for (uint64_t j = 0; j < col; j += 16) { __m512 a = _mm512_loadu_ps(&(t1[i*col + j])); __m512 b = _mm512_loadu_ps(&(t2[j])); sumx16 = _mm512_fmadd_ps(a, b, sumx16); } outx16[i] = _mm512_reduce_add_ps(sum16); } return outx16;} |
ほとんどのスカラー式は、ベクトルで同じ演算を行う組込み関数呼び出しに置き換えられています。
sum のゼロ初期化を、16 個のゼロ要素のベクトルを作成する _mm512_set1_ps() (英語) 呼び出しに置き換え、それを sumx16 に割り当てます。最も内側のループ内で、_mm512_loadu_ps() (英語) を使用して t1 と t2 の16 個の要素をそれぞれ変数 a と b にロードします。_mm512_fmadd_ps() (英語) 関数を使用して、a と b の各要素の積を sumx16 の対応する要素に加算します。
内部ループの終わりでは、sumx16 には単一の和ではなく、16 個の部分和が格納されています。最終的な結果を求めるには、配列平均値の例で使用した _mm512_reduce_add_ps() (英語) 関数を呼び出して、これら 16 個の要素を加算する必要があります。
浮動小数点と実数
始めに、ベクトルバージョンとスカラーバ―ションは全く同じ計算を行わない可能性があることを留意してください。実数を使用してこの計算を行う場合、部分積を加算する順番は問題となりませんが、浮動小数点値では問題となります。浮動小数点値を加算すると、結果を正確に浮動小数点値として表現できないことがあります。その場合、結果を表現可能な 2 つの値のうち最も近い値に丸める必要があります。正確な結果と表現可能な結果の差は、丸めによる誤差によるものです。
浮動小数点値の積の合計を計算する場合、正確な結果と丸め誤差による合計の計算結果は異なります。ベクトル化された行列の積和では、スカラーバージョンとは異なる順番で部分積が計算されるため、それぞれの加算の丸め誤差が異なる可能性があります。さらに、_mm512_fmadd_ps() (英語) 関数は、部分積を部分和に加算する前に丸めを行わないため、加算のみの丸め誤差が生じます。スカラー計算とベクトル計算で丸め誤差が異なる場合、結果も異なる可能性があります。しかし、これはどちらかが誤りであるということを意味するものではありません。浮動小数点計算の特殊性を示すだけです。
マンデルブロ集合
マンデルブロ集合は、次の反復で定義される数列が無限大に発散しないという条件を満たす複素数 z の集合です。
z(0) = z, z(n+1) = z(n)*z(n) + z, n=0,1,2, …
つまり、すべての反復 z(n) の絶対値が B より大きくならない数 B があることを意味します。マンデルブロ集合の計算は、集合内にない点のカラフルなイメージを描画する際に使用されます。それぞれの表示色は上限を超えるために必要な項の数を示します。この計算は、ベクトル計算のパフォーマンスを実証する例としてよく利用されます。B が 2.0 であるマンデルブロ集合 (https://github.com/ispc/ispc/blob/master/examples/mandelbrot_tasks/mandelbrot_tasks_serial.cpp) を計算するカーネルコードを入手できます。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 | static int mandel(float c_re, float c_im, int count) { float z_re = c_re, z_im = c_im; int i; for (i = 0; i < count; ++i) { if (z_re * z_re + z_im * z_im > 4.f) break; float new_re = z_re*z_re - z_im*z_im; float new_im = 2.f * z_re * z_im; z_re = c_re + new_re; z_im = c_im + new_im; }return i;} |
無限級数のすべての項を評価することは不可能であるため、この関数は count で指定される上限数までしか評価しません。戻り値は、発散しなかった項の数を示し、通常はその点の表示色を選択するために使用されます。関数が count 数を返す場合、その点はマンデルブロ集合内にあると見なされます。
このコードをベクトル化するには、行列ベクトル乗算でベクトル化したのと同じ手法で各スカラー計算を等価なベクトルに置き換えます。しかし、次のソース行は複雑です: “if (z_re * z_re + z_im * z_im > 4.0f) break;”。条件ブレークをどのようにベクトル化したらよいでしょう?
この例では、級数が上限を超えると、それ以降のすべての項も上限を超えることになるので、すべての要素が上限に達するまで、または反復上限に達するまで、無条件にすべての要素の計算を続行できます。ベクトルを比較して上限を超えた要素をマスクし、残りの結果を更新することで条件式を処理できます。以下は、インテル® アドバンスト・ベクトル・エクステンション 2 (インテル® AVX2) 関数を使用したバージョンのコードです。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 | /* インテル(R) AVX2 の実装 */__m256i avx2Mandel (__m256 c_re8, __m256 c_im8, uint32_t max_iterations) { __m256 z_re8 = c_re8; __m256 z_im8 = c_im8; __m256 four8 = _mm256_set1_ps(4.0f); __m256 two8 = _mm256_set1_ps(2.0f); __m256i result = _mm256_set1_epi32(0); __m256i one8 = _mm256_set1_epi32(1); for (auto i = 0; i < max_iterations; i++) { __m256 z_im8sq = _mm256_mul_ps(z_im8, z_im8); __m256 z_re8sq = _mm256_mul_ps(z_re8, z_re8); __m256 new_im8 = _mm256_mul_ps(z_re8, z_im8); __m256 z_abs8sq = _mm256_add_ps(z_re8sq, z_im8sq); __m256 new_re8 = _mm256_sub_ps(z_re8sq, z_im8sq); __m256 mi8 = _mm256_cmp_ps(z_abs8sq, four8, _CMP_LT_OQ); z_im8 = _mm256_fmadd_ps(two8, new_im8, c_im8); z_re8 = _mm256_add_ps(new_re8, c_re8); int mask = _mm256_movemask_ps(mi8); __m256i masked1 = _mm256_and_si256(_mm256_castps_si256(mi8), one8); if (0 == mask) break; result = _mm256_add_epi32(result, masked1); } return result;}; |
スカラー関数は、結果が発散するまでの計算に要した反復回数を返すため、ベクトル関数も同じ値のベクトルを返す必要があります。要素が上限を超えていないことを示すベクトル mi8 を最初に生成することで、これらを計算します。このベクトルの各要素は、ずべて 0 (ゼロ) のビット (テスト条件 _CMP_LT_OQ が真でない場合)、またはすべて 1 のビット (真である場合) のいずれかです。ベクトルがすべてゼロであれば、すべてが発散しているためループから抜けることができます。それ以外では、ベクトル値は _mm256_castps_si256 関数で 32 ビット整数値のベクトルに再解釈され、ビットが立った 32 ビットのベクトルでマスクされます。これは、発散していないすべての要素に対し 1 を、まだ発散していない要素に対し 0 を返します。残りの処理は、そのベクトルをベクトル・アキュムレーターの結果に加算するだけです。
この関数のインテル® AVX-512 バージョンも似ていますが、1 つ大きな違いがあります。_mm256_cmp_ps 関数は、__m256 型のベクトル値を返します。__m512 型のベクトルを返す _mm512_cmp_ps 関数を使用することが想定されますが、この関数は存在しません。代わりに、__mmask16 型の値を返す _mm512_cmp_ps_mask 関数を使用します。これは、各ビットがベクトルの 1 つの要素を示す 16 ビット値です。これらの値は、ベクトル条件式の実行で使用される 8 つのマスクレジスターにそれぞれ格納されます。インテル® AVX2 関数で結果に加算される値を計算する場合、インテル® AVX-512 では _mm512_mask_add_epi32 関数を使用して直接加算するためマスクを使用できます。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 | /* AVX512 Implementation */__m512i avx512Mandel(__m512 c_re16, __m512 c_im16, uint32_t max_iterations) { __m512 z_re16 = c_re16; __m512 z_im16 = c_im16; __m512 four16 = _mm512_set1_ps(4.0f); __m512 two16 = _mm512_set1_ps(2.0f); __m512i one16 = _mm512_set1_epi32(1); __m512i result = _mm512_setzero_si512(); for (auto i = 0; i < max_iterations; i++) { __m512 z_im16sq = _mm512_mul_ps(z_im16, z_im16); __m512 z_re16sq = _mm512_mul_ps(z_re16, z_re16); __m512 new_im16 = _mm512_mul_ps(z_re16, z_im16); __m512 z_abs16sq = _mm512_add_ps(z_re16sq, z_im16sq); __m512 new_re16 = _mm512_sub_ps(z_re16sq, z_im16sq); __mmask16 mask = _mm512_cmp_ps_mask(z_abs16sq, four16, _CMP_LT_OQ); z_im16 = _mm512_fmadd_ps(two16, new_im16, c_im16); z_re16 = _mm512_add_ps(new_re16, c_re16); if (0 == mask) break; result = _mm512_mask_add_epi32(result, mask, result, one16); } return result;}; |
ベクトル化されたマンデルブロ集合の計算では、スカラーの代わりにベクトル値を返し、それぞれの値はスカラー関数が返す値と同一です。戻り値が、実数と虚数の引数ベクトルとは異なる型であることに気が付かれたかもしれません。スカラー関数の引数は float 型で、符号なしの整数を返します。ベクトル関数の引数は float 型のベクトルバージョンで、戻り値は 32 ビットの符号なし整数を保持するベクトルです。double 型を使用する関数をベクトル化する場合、double 型の要素を保持するベクトル型も用意されています: __m128d、__m256d、および __m512。しかし、signed char や unsigned short などその他の整数型のベクトルバージョンはありません。__m128i、__m256i、および __m512i 型のベクトルは、サイズや符号にかかわりなくすべての整数要素で使用できます。
特定の型を保持するベクトルを、異なる型の要素を持つベクトルに変換またはキャスト (再解釈) することもできます。mandelx8 関数は、_mm256_castps_si256 関数を使用して、比較関数の結果 __m256 を、結果ベクトルを更新するため __m256i 整数要素マスクとして再解釈します。
インテル® AVX-512 のパフォーマンス
パフォーマンスを比較するため、インテル® AVX、インテル® AVX2、およびインテル® AVX-512 組込み関数を使用して、マンデルブロ、行列ベクトル乗算、そして配列平均カーネル関数の実行時間を測定しました。ソースコードは、/O2 オプションでコンパイルされています。テスト・プラットフォームでは、インテル® AVX-512 を使用したマンデルブロは、インテル® AVX2 のサンプルバージョンよりも 1.77 倍1 高速です。インテル® AVX2 バージョンと比較して、配列平均 (ソースコード) は 1.911 倍高速で、行列ベクトル乗算 (ソースコード) は 1.801 倍高速です。
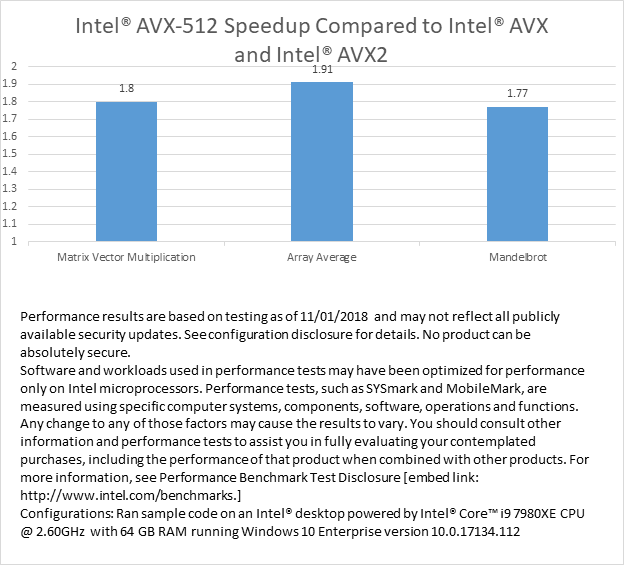
インテル® AVX-512 で達成可能な理論上のパフォーマンスは、インテル® AVX2 の 2 倍になるはずです。この検証でそこまで達しないのには、いくつかの理由があります。1 つは、計算の最も内側のループだけがインテル® AVX-512 命令でスピードアップされ、合計実行時間には外部ループの実行に費やされた時間とその他のオーバーヘッドが含まれるためです。もう 1 つの理由は、有限リソースであるメモリーシステムの帯域幅が計算を行うすべてのコア間で共有されるためです。帯域幅を使い切ると、プロセッサーの計算はデータの移動に制約されます。
まとめ
インテル® AVX2 とインテル® AVX-512 関数を使用してマンデルブロ集合を計算するコードを示すとともに、配列平均および行列ベクトル乗算をベクトル化する例を紹介しました。このコードは、以前の記事のサンプルコードよりもインテル® AVX-512 の使い方をより実践的に示しています。テスト・プラットフォームで測定されたデータから、インテル® AVX-512 のコードはインテル® AVX2 のコードと比較して、77% ~ 91% のパフォーマンス向上をもたらすことが分かります。
インテル® AVX-512 は、インテル® AVX2 と比べて、1 命令で処理できるデータを 2 倍にすることで、インテル® ハードウェアの能力を最大限に活用してパフォーマンスを向上させます。この機能は、人工知能、ディープラーニング、科学シミュレーション、財務分析、3D モデリング、画像/音声/ビデオ処理、およびデータ圧縮で利用できます。インテル® AVX-512 を使用すると、アプリケーションの潜在能力を最大限に引き出すことができます。
(1) 性能に関するテストに使用されるソフトウェアとワークロードは、性能がインテル® マイクロプロセッサー用に最適化されていることがあります。SYSmark* や MobileMark* などの性能テストは、特定のコンピューター・システム、コンポーネント、ソフトウェア、操作、機能に基づいて行ったものです。結果はこれらの要因によって異なります。製品の購入を検討される場合は、他の製品と組み合わせた場合の本製品の性能など、ほかの情報や性能テストも参考にして、パフォーマンスを総合的に評価することをお勧めします。§ 構成: サンプルコードは、インテル® Core™ i9-7980XE エクストリーム・エディション・プロセッサー @ 2.60Ghz、64 GB RAM を搭載するデスクトップ・システム上の Windows® 10 Enterprise バージョン 10.0.17134.112 で実行されました。 § 詳細は、https://www.intel.com/content/www/us/en/benchmarks/benchmark.html (英語) をご覧ください。
コンパイラーの最適化に関する詳細は、最適化に関する注意事項を参照してください。

