インテル® アーキテクチャーの SIMD テクノロジーによりゲームコードを高速化

2014.03.06
ゲームスマートフォンタブレット
AndroidAVX/AVX2ISA

この記事は、インテル® デベロッパー・ゾーンに掲載されている「Using SIMD Technologies on Intel® Architecture to Speed Up Game Code」(http://software.intel.com/en-us/articles/using-simd-technologies-on-intel-architecture-to-speed-up-game-code) の日本語参考訳です。

概要

2D/3D ゲームの開発と実行には多数の複雑な数学演算が不可欠です。これらの演算では、多くのベクトルおよび行列変換が行われるため、高い計算能力が必要になります。この記事では、行列乗算の種類を確認した後、実際のケースとして、中国で有名な Android* ベースの 3D シューティング・ゲーム「The Last Defender」の数学演算を、インテル® アーキテクチャー (IA) の SIMD テクノロジーであるインテル® ストリーミング SIMD 拡張命令 X (インテル® SSE[2,3,4.1,4.2]) およびインテル® ストリーミング SIMD 拡張命令 3 補足命令 (インテル® SSSE3) やインテル® アドバンスト・ベクトル拡張命令 (インテル® AVX) を使用して高速化し、ゲームのパフォーマンスを向上する方法を説明します。記事の最後では、IA コードベースの一般的な最適化ソリューションについても触れています。

はじめに

SIMD (Single Instruction Multiple Data) は、1 つの命令で複数のデータ計算を行う、命令レベルの並列計算テクノロジーの 1 つです。並列計算をフルに活用する能力を備えたインテル® SSE は、ベクトルや行列の各要素を個別に計算できるため、ゲームコードのベクトル演算および行列演算に最適です (開発者は、各要素が互いに干渉しないことを確認する必要があります)。これは、各要素で 1 つの命令サイクル (例えば、4×4 行列ではすべての演算を実行するのに 16 サイクル) が必要な従来のシリアル計算テクノロジーとは対照的です。SIMD テクノロジーを利用して SIMD 実装が 1 つの命令サイクルで 4 つのデータ演算を並列に処理できると仮定すると、1 つの命令サイクルで同時に 4 つの要素の演算を完了できるため、16 の要素の演算を 4 つの命令サイクルで完了できることになります。

インテル® SSE 命令は IA の SIMD 実装で広く利用されており、特にゲームエンジンでよく見かけます。インテル® SSE には、SSE、SSE2、SSE3、SSE4.x、AVX、AVX2 などの拡張命令があり、多くの種類の整数および浮動小数点演算をサポートしています。また、効率良いメモリーアクセスもサポートしています。この記事では、単純にこれらのすべての拡張命令をインテル® SSE と表記し、行列乗算で使用する方法について説明します。

メモリーの行列格納モデルは 2 種類あります。

  1. 列優先 (図 1) では、行列のすべての要素は列順でメモリーに 1 つずつ格納されます。メモリーアクセスに連続アドレッシングが使用されると、行列の要素は列ごとにアクセスされます。OpenGL* は、この手法で行列をメモリーに格納しています。


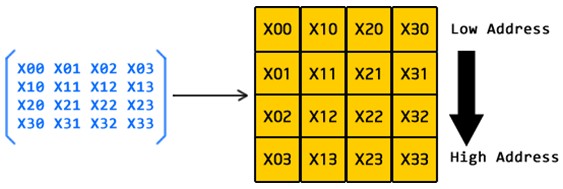
    図 1. 列優先

  2. 行優先 (図 2) では、行列のすべての要素は行順でメモリーに 1 つずつ格納されます。メモリーアクセスに連続アドレッシングが使用されると、行列の要素は行ごとにアクセスされます。「The Last Defender」ゲームは、高レベルの行列格納モデルとしてこの手法を採用しています。


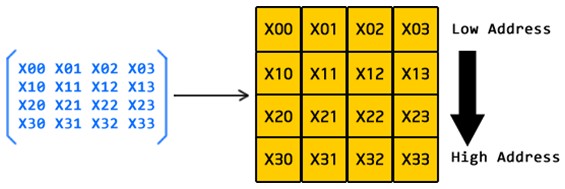
    図 2. 行優先

この記事では、Android* ゲーム開発の利用例として行優先の「The Last Defender」を取り上げていますが、OpenGL* ES (列優先) は Android* における唯一の低レベル・グラフィック・ハードウェア・アクセラレーションであるため、両方の格納モデルと最適化について説明します。

次の説明で、OpenGL* ES と「The Last Defender」の行列乗算 (ベクトル変換) の順序は同じです。この式 (V はベクトル、M は行列) が示すように、どちらも行列の前乗算を行っています。

Vo = Mn x … x M2 x M1 x Vi

図 3 を参照してください。


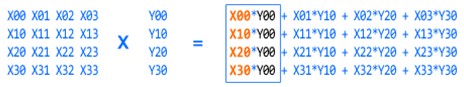
図 3. MxV

図 3 は、MxV の結果である新しいベクトルを示しています。4×4 の行列と 4 要素のベクトルを乗算するため、16 個の乗算と 12 個の加算が必要になります。大量の計算が行われるため、シリアルに実行すると多くの命令サイクルが必要になり、長い時間がかかります。ゲームエンジンでは、特にこの種の演算が大量に行われるため、最適化の鍵となる部分です。

図 3 の青枠の 4 つの要素は同時に計算できます。これにより、MxV 全体で必要な計算が 4 つの並列乗算と 3 つの並列加算のみ (つまり、1/4) になるため、4 倍のパフォーマンス向上を期待できます。実際、図 4 に示すように、インテル® SSE は、各列ですべての乗算と加算を効率良く並列実行します。


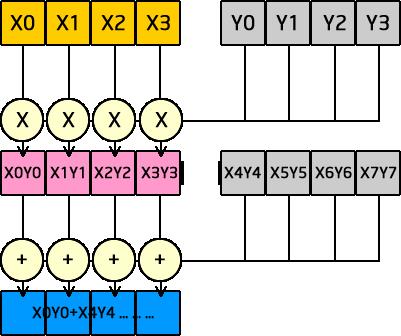
図 4. 行列の並列演算


図 5. 行列 X 行列

図 5 は、前に示したベクトルと行列の乗算を拡張した、2 つの行列の乗算の例です。この演算は、行列格納モデルによって影響を受けることを知っておくことが重要です。図 5 の異なる枠色は、2 つの行列格納モデルの並列演算を示しています。ピンクは行優先モデルの並列演算を、オレンジは列優先モデルの並列演算を示しています。インテル® SSE は、行列格納モデルが異なる場合でも効率良いメモリーアクセス命令を提供するため、これを利用するべきでしょう。ただし、メモリーアクセス命令のメモリー・アライメント制限に注意する必要があります。

次に、各行列格納モデルに基づく 2 つのソリューションを示します。どちらのソリューションも、インテル® SSE で行列演算を並列化し、コードの実行を高速化します。

「The Last Defender」の行列乗算を行優先で最適化する

「The Last Defender」ゲームのコードをインテル® SSE で最適化する前に、インテル® VTune™ Amplifier 2011 for Android を使用して、図 6 のように Matrix4f::mul 関数の計算消費をプロファイルしました。


図 6. オリジナル (ベースライン) の Matrix4f::mul の計算消費リファレンス

コードのプロファイルは Motorola* MT788 スマートフォン (インテル® Atom™ プロセッサー Z2480 搭載) で行いました。ある操作の後、Matrix4f::mul の計算消費リファレンスは 83,340,000 となり、非常に時間のかかる計算であることが分かりました。以下に、実際のコードを示します。

void Matrix4f::mul(Matrix4f *m1, Matrix4f *m2)
	if (this != m1 && this != m2)
	{

		this->f[m00] = m1->f[m00] * m2->f[m00] + m1->f[m01] * m2->f[m10] + 
					   m1->f[m02] * m2->f[m20] + m1->f[m03] * m2->f[m30];
		this->f[m01] = m1->f[m00] * m2->f[m01] + m1->f[m01] * m2->f[m11] + 
					   m1->f[m02] * m2->f[m21] + m1->f[m03] * m2->f[m31];
		this->f[m02] = m1->f[m00] * m2->f[m02] + m1->f[m01] * m2->f[m12] + 
					   m1->f[m02] * m2->f[m22] + m1->f[m03] * m2->f[m32];
		this->f[m03] = m1->f[m00] * m2->f[m03] + m1->f[m01] * m2->f[m13] + 
					   m1->f[m02] * m2->f[m23] + m1->f[m03] * m2->f[m33];

		this->f[m10] = m1->f[m10] * m2->f[m00] + m1->f[m11] * m2->f[m10] + 
					   m1->f[m12] * m2->f[m20] + m1->f[m13] * m2->f[m30];
		this->f[m11] = m1->f[m10] * m2->f[m01] + m1->f[m11] * m2->f[m11] + 
					   m1->f[m12] * m2->f[m21] + m1->f[m13] * m2->f[m31];
		this->f[m12] = m1->f[m10] * m2->f[m02] + m1->f[m11] * m2->f[m12] + 
					   m1->f[m12] * m2->f[m22] + m1->f[m13] * m2->f[m32];
		this->f[m13] = m1->f[m10] * m2->f[m03] + m1->f[m11] * m2->f[m13] + 
					   m1->f[m12] * m2->f[m23] + m1->f[m13] * m2->f[m33];

		this->f[m20] = m1->f[m20] * m2->f[m00] + m1->f[m21] * m2->f[m10] + 
					   m1->f[m22] * m2->f[m20] + m1->f[m23] * m2->f[m30];
		this->f[m21] = m1->f[m20] * m2->f[m01] + m1->f[m21] * m2->f[m11] + 
					   m1->f[m22] * m2->f[m21] + m1->f[m23] * m2->f[m31];
		this->f[m22] = m1->f[m20] * m2->f[m02] + m1->f[m21] * m2->f[m12] + 
					   m1->f[m22] * m2->f[m22] + m1->f[m23] * m2->f[m32];
		this->f[m23] = m1->f[m20] * m2->f[m03] + m1->f[m21] * m2->f[m13] + 
					   m1->f[m22] * m2->f[m23] + m1->f[m23] * m2->f[m33];

		this->f[m30] = m1->f[m30] * m2->f[m00] + m1->f[m31] * m2->f[m10] + 
					   m1->f[m32] * m2->f[m20] + m1->f[m33] * m2->f[m30];
		this->f[m31] = m1->f[m30] * m2->f[m01] + m1->f[m31] * m2->f[m11] + 
					   m1->f[m32] * m2->f[m21] + m1->f[m33] * m2->f[m31];
		this->f[m32] = m1->f[m30] * m2->f[m02] + m1->f[m31] * m2->f[m12] + 
					   m1->f[m32] * m2->f[m22] + m1->f[m33] * m2->f[m32];
		this->f[m33] = m1->f[m30] * m2->f[m03] + m1->f[m31] * m2->f[m13] + 
					   m1->f[m32] * m2->f[m23] + m1->f[m33] * m2->f[m33];
	}
	else
	{
		float _m00, _m01, _m02, _m03, _m10, _m11, _m12, _m13, _m20, _m21, 
			  _m22, _m23, _m30, _m31, _m32, _m33; // vars
		// for
		// te_mp
		// result
		// _matrix
		_m00 = m1->f[m00] * m2->f[m00] + m1->f[m01] * m2->f[m10] + 
			   m1->f[m02] * m2->f[m20] + m1->f[m03] * m2->f[m30];
		_m01 = m1->f[m00] * m2->f[m01] + m1->f[m01] * m2->f[m11] + 
			   m1->f[m02] * m2->f[m21] + m1->f[m03] * m2->f[m31];
		_m02 = m1->f[m00] * m2->f[m02] + m1->f[m01] * m2->f[m12] + 
			   m1->f[m02] * m2->f[m22] + m1->f[m03] * m2->f[m32];
		_m03 = m1->f[m00] * m2->f[m03] + m1->f[m01] * m2->f[m13] + 
			   m1->f[m02] * m2->f[m23] + m1->f[m03] * m2->f[m33];

		_m10 = m1->f[m10] * m2->f[m00] + m1->f[m11] * m2->f[m10] + 
			   m1->f[m12] * m2->f[m20] + m1->f[m13] * m2->f[m30];
		_m11 = m1->f[m10] * m2->f[m01] + m1->f[m11] * m2->f[m11] + 
			   m1->f[m12] * m2->f[m21] + m1->f[m13] * m2->f[m31];
		_m12 = m1->f[m10] * m2->f[m02] + m1->f[m11] * m2->f[m12] + 
			   m1->f[m12] * m2->f[m22] + m1->f[m13] * m2->f[m32];
		_m13 = m1->f[m10] * m2->f[m03] + m1->f[m11] * m2->f[m13] + 
			   m1->f[m12] * m2->f[m23] + m1->f[m13] * m2->f[m33];

		_m20 = m1->f[m20] * m2->f[m00] + m1->f[m21] * m2->f[m10] + 
			   m1->f[m22] * m2->f[m20] + m1->f[m23] * m2->f[m30];
		_m21 = m1->f[m20] * m2->f[m01] + m1->f[m21] * m2->f[m11] + 
			   m1->f[m22] * m2->f[m21] + m1->f[m23] * m2->f[m31];
		_m22 = m1->f[m20] * m2->f[m02] + m1->f[m21] * m2->f[m12] + 
			   m1->f[m22] * m2->f[m22] + m1->f[m23] * m2->f[m32];
		_m23 = m1->f[m20] * m2->f[m03] + m1->f[m21] * m2->f[m13] + 
			   m1->f[m22] * m2->f[m23] + m1->f[m23] * m2->f[m33];

		_m30 = m1->f[m30] * m2->f[m00] + m1->f[m31] * m2->f[m10] + 
			   m1->f[m32] * m2->f[m20] + m1->f[m33] * m2->f[m30];
		_m31 = m1->f[m30] * m2->f[m01] + m1->f[m31] * m2->f[m11] + 
			   m1->f[m32] * m2->f[m21] + m1->f[m33] * m2->f[m31];
		_m32 = m1->f[m30] * m2->f[m02] + m1->f[m31] * m2->f[m12] + 
			   m1->f[m32] * m2->f[m22] + m1->f[m33] * m2->f[m32];
		_m33 = m1->f[m30] * m2->f[m03] + m1->f[m31] * m2->f[m13] + 
			   m1->f[m32] * m2->f[m23] + m1->f[m33] * m2->f[m33];

		this->f[m00] = _m00;
		this->f[m01] = _m01;
		this->f[m02] = _m02;
		this->f[m03] = _m03;
		this->f[m10] = _m10;
		this->f[m11] = _m11;
		this->f[m12] = _m12;
		this->f[m13] = _m13;
		this->f[m20] = _m20;
		this->f[m21] = _m21;
		this->f[m22] = _m22;
		this->f[m23] = _m23;
		this->f[m30] = _m30;
		this->f[m31] = _m31;
		this->f[m32] = _m32;
		this->f[m33] = _m33;
	}

ご覧のとおり、このコードは明確で単純です。しかし、コードに長い時間がかかっていることも明らかでした。この関数はゲームエンジンで頻繁に呼び出され、パフォーマンスに影響を与えていることから、この部分を最適化の最初の候補にしました。

前述のように、インテル® SSE による単純な最適化を (行優先で) 適用しました。

	__m128 m1_row_0 = _mm_setr_ps(m1->f[m00], m1->f[m01], m1->f[m02], 
								  m1->f[m03]);
	__m128 m1_row_1 = _mm_setr_ps(m1->f[m10], m1->f[m11], m1->f[m12], 
								  m1->f[m13]);
	__m128 m1_row_2 = _mm_setr_ps(m1->f[m20], m1->f[m21], m1->f[m22], 
								  m1->f[m23]);
	__m128 m1_row_3 = _mm_setr_ps(m1->f[m30], m1->f[m31], m1->f[m32], 
								  m1->f[m33]);

	__m128 m2_row_0 = _mm_setr_ps(m2->f[m00], m2->f[m01], m2->f[m02], 
								  m2->f[m03]);
	__m128 m2_row_1 = _mm_setr_ps(m2->f[m10], m2->f[m11], m2->f[m12], 
								  m2->f[m13]);
	__m128 m2_row_2 = _mm_setr_ps(m2->f[m20], m2->f[m21], m2->f[m22], 
								  m2->f[m23]);
	__m128 m2_row_3 = _mm_setr_ps(m2->f[m30], m2->f[m31], m2->f[m32], 
								  m2->f[m33]);

	__m128 out0;
	__m128 out1;
	__m128 out2;
	__m128 out3;

	out0 = _mm_mul_ps(m2_row_0, _mm_replicate_x_ps(m1_row_0));
	out1 = _mm_mul_ps(m2_row_0, _mm_replicate_x_ps(m1_row_1));
	out2 = _mm_mul_ps(m2_row_0, _mm_replicate_x_ps(m1_row_2));
	out3 = _mm_mul_ps(m2_row_0, _mm_replicate_x_ps(m1_row_3));

	out0 = _mm_madd_ps(m2_row_1, _mm_replicate_y_ps(m1_row_0), out0);
	out1 = _mm_madd_ps(m2_row_1, _mm_replicate_y_ps(m1_row_1), out1);
	out2 = _mm_madd_ps(m2_row_1, _mm_replicate_y_ps(m1_row_2), out2);
	out3 = _mm_madd_ps(m2_row_1, _mm_replicate_y_ps(m1_row_3), out3);

	out0 = _mm_madd_ps(m2_row_2, _mm_replicate_z_ps(m1_row_0), out0);
	out1 = _mm_madd_ps(m2_row_2, _mm_replicate_z_ps(m1_row_1), out1);
	out2 = _mm_madd_ps(m2_row_2, _mm_replicate_z_ps(m1_row_2), out2);
	out3 = _mm_madd_ps(m2_row_2, _mm_replicate_z_ps(m1_row_3), out3);

	out0 = _mm_madd_ps(m2_row_3, _mm_replicate_w_ps(m1_row_0), out0);
	out1 = _mm_madd_ps(m2_row_3, _mm_replicate_w_ps(m1_row_1), out1);
	out2 = _mm_madd_ps(m2_row_3, _mm_replicate_w_ps(m1_row_2), out2);
	out3 = _mm_madd_ps(m2_row_3, _mm_replicate_w_ps(m1_row_3), out3);

	_mm_store_ps(&this->f[0], out0);
	_mm_store_ps(&this->f[4], out1);
	_mm_store_ps(&this->f[8], out2);
	_mm_store_ps(&this->f[12], out3);

この実装は、インテル® SSE 組込み関数を使用しています。コンパイラーがインテル® SSE 組込み関数をサポートしている場合は、アセンブリー言語でコーディングする代わりにインテル® SSE 組込み関数を使用することを推奨します。アセンブリー言語よりも簡単に使用でき、より直感的で、パフォーマンスが損なわれることもありません。

__m128 は、インテル® SSE 組込み関数のデータ型です。長さは 128 バイトで、4 つの 32 ビット単精度浮動小数点値を格納できます。

__m128 _mm_setr_ps(float z , float y , float x , float w );

この組込み関数は、r0 := z、r1 := y、r2 := x、r3 := w のように、1 つの __m128 データの 4 つの単精度浮動小数点値を設定します。

__m128 _mm_mul_ps(__m128 a , __m128 b );

この組込み関数は、a の 4 つの単精度浮動小数点値と b の 4 つの単精度浮動小数点値を並列に乗算します。

r0 := a0 * b0
r1 := a1 * b1
r2 := a2 * b2
r3 := a3 * b3

_mm_replicate_(x~w)_ps は次の内容を含むマクロです。
#define _mm_replicate_x_ps(v) \
_mm_shuffle_ps((v), (v), SHUFFLE_PARAM(0, 0, 0, 0))

#define _mm_replicate_y_ps(v) \
_mm_shuffle_ps((v), (v), SHUFFLE_PARAM(1, 1, 1, 1))

#define _mm_replicate_z_ps(v) \
_mm_shuffle_ps((v), (v), SHUFFLE_PARAM(2, 2, 2, 2))

#define _mm_replicate_w_ps(v) \
_mm_shuffle_ps((v), (v), SHUFFLE_PARAM(3, 3, 3, 3))

__m128 _mm_shuffle_ps(__m128 a , __m128 b , int i );

この組込み関数は、マスク i に使用しています。a および b から 4 つの特定の単精度浮動小数点値を選択し、マスク i に基づいて新しい __m128 データに並べ替えを行います。マスクは即値でなければいけません。図 7 に詳細な規則を示します。

_MM_SHUFFLE(z, y, x, w)
/* 次の値に展開 */
(z<<6) | (y<<4) | (x<<2) | w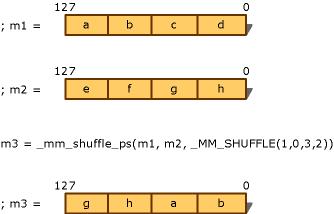


図 7. SHUFFLE マクロ

次の SHUFFLE マクロを使用して The Last Defender を最適化しました。

#define SHUFFLE_PARAM(x, y, z, w) \
((x) | ((y) << 2) | ((z) << 4) | ((w) << 6))

同じ要素の値を同時に計算するため、4 つの同じ単精度浮動小数点値を 1 つの __m128 データに設定します。

#define _mm_madd_ps(a, b, c) \
_mm_add_ps(_mm_mul_ps((a), (b)), (c))

このマクロは、乗算 (先) と加算 (後) の組み合わせを実装して、コーディングを容易にします。

void _mm_store_ps(float *p, __m128 a );

この組込み関数は、メモリーアクセスを行い、__m128 データをアドレス p に格納します (アドレス p は 16 バイトでアライメントされている必要があります)。

p[0] := a0
p[1] := a1
p[2] := a2
p[3] := a3

この簡単な最適化の後、インテル® VTune™ Amplifier 2011 for Android を使用して同じ演算を再度プロファイルしたところ、図 8 の結果が得られました。


図 8. 最適化された Matrix4f::mul の計算消費リファレンス

計算消費リファレンスが 83,340,000 から 18,780,000 に減少し、パフォーマンスが 4 倍以上も向上しました1。同じテスト手順と計算を同じシナリオ (同じシーン、ほぼ同じ敵、同じ車両、同じ武器、同じテスト期間など) で実行しましたが、AI と敵の数の違いがテスト結果にわずかに影響しただけでした。この例は、インテル® SSE の並列計算能力の高さを表しています。

OpenGL* ES の列優先乗算を最適化する

OpenGL* ES ベースのアプリケーションの行列演算では、列優先格納モデルを使用することを推奨します。このモデルは OpenGL* ES の仕様を満たしているだけでなく、並列化をより簡単に行えます。前述したように、多くの効率良いメモリー・アクセス・テクノロジーを通じてコードを最適化できます。次のコードは、ARM NEON* からインテル® SSE への典型的な変換サンプルです。

void NEON_Matrix4Mul(const float* a, const float* b, float* output )
{
    __asm__ volatile
    (
     // A & B を格納。q4-q7 用の空間を残す
     "vldmia %1, { q0-q3 } nt"
     "vldmia %2, { q8-q11 }nt"

     // 結果 = B の 1 列目 x A の 1 行目
     "vmul.f32 q12, q8, d0[0]nt"
     "vmul.f32 q13, q8, d2[0]nt"
     "vmul.f32 q14, q8, d4[0]nt"
     "vmul.f32 q15, q8, d6[0]nt"

     // 結果 += B の 2 列目 x A の 2 行目
     "vmla.f32 q12, q9, d0[1]nt"
     "vmla.f32 q13, q9, d2[1]nt"
     "vmla.f32 q14, q9, d4[1]nt"
     "vmla.f32 q15, q9, d6[1]nt"

     // 結果 += B の 3 列目 x A の 3 行目
     "vmla.f32 q12, q10, d1[0]nt"
     "vmla.f32 q13, q10, d3[0]nt"
     "vmla.f32 q14, q10, d5[0]nt"
     "vmla.f32 q15, q10, d7[0]nt"

     // 結果 += B の 最終列 x A の 最終行
     "vmla.f32 q12, q11, d1[1]nt"
     "vmla.f32 q13, q11, d3[1]nt"
     "vmla.f32 q14, q11, d5[1]nt"
     "vmla.f32 q15, q11, d7[1]nt"

     // output = 結果のレジスター
     "vstmia %0, { q12-q15 }"
     : // output なし
     : "r" (output), "r" (a), "r" (b)  // input - ポインターの「値」は変わらない
     : "memory", "q0", "q1", "q2", "q3", "q8", "q9", "q10", "q11", "q12", 
       "q13", "q14", "q15" //clobber
     );
}
//##########################################################################
static inline void SSE_Matrix4Mul(const float* a, const float* b, float* output)
{
	// OpenGL* ES (列優先) のため、行列 a と b をロード
	__m128 ma_col_0 = _mm_load_ps(a);
	__m128 ma_col_1 = _mm_load_ps(a + 4);
	__m128 ma_col_2 = _mm_load_ps(a + 8);
	__m128 ma_col_3 = _mm_load_ps(a + 12);

	__m128 mb_col_0 = _mm_load_ps(b);
	__m128 mb_col_1 = _mm_load_ps(b + 4);
	__m128 mb_col_2 = _mm_load_ps(b + 8);
	__m128 mb_col_3 = _mm_load_ps(b + 12);

	// 結果を格納する準備
	__m128 result0;
	__m128 result1;
	__m128 result2;
	__m128 result3;

	// 結果 = B の 1 列目 x A の 1 行目
	result0 = _mm_mul_ps(mb_col_0, _mm_replicate_x_ps(ma_col_0));
	result1 = _mm_mul_ps(mb_col_0, _mm_replicate_x_ps(ma_col_1));
	result2 = _mm_mul_ps(mb_col_0, _mm_replicate_x_ps(ma_col_2));
	result3 = _mm_mul_ps(mb_col_0, _mm_replicate_x_ps(ma_col_3));

	// 結果 += B の 2 列目 x A の 2 行目
	result0 = _mm_madd_ps(mb_col_1, _mm_replicate_y_ps(ma_col_0), result0);
	result1 = _mm_madd_ps(mb_col_1, _mm_replicate_y_ps(ma_col_1), result1);
	result2 = _mm_madd_ps(mb_col_1, _mm_replicate_y_ps(ma_col_2), result2);
	result3 = _mm_madd_ps(mb_col_1, _mm_replicate_y_ps(ma_col_3), result3);

	// 結果 += B の 3 列目 x A の 3 行目
	result0 = _mm_madd_ps(mb_col_2, _mm_replicate_z_ps(ma_col_0), result0);
	result1 = _mm_madd_ps(mb_col_2, _mm_replicate_z_ps(ma_col_1), result1);
	result2 = _mm_madd_ps(mb_col_2, _mm_replicate_z_ps(ma_col_2), result2);
	result3 = _mm_madd_ps(mb_col_2, _mm_replicate_z_ps(ma_col_3), result3);

	// 結果 += B の 最終列 x A の 最終行
	result0 = _mm_madd_ps(mb_col_3, _mm_replicate_w_ps(ma_col_0), result0);
	result1 = _mm_madd_ps(mb_col_3, _mm_replicate_w_ps(ma_col_1), result1);
	result2 = _mm_madd_ps(mb_col_3, _mm_replicate_w_ps(ma_col_2), result2);
	result3 = _mm_madd_ps(mb_col_3, _mm_replicate_w_ps(ma_col_3), result3);

	// 結果をメモリーへ格納
	_mm_store_ps(output, result0);
	_mm_store_ps(output+4, result1);
	_mm_store_ps(output+8, result2);
	_mm_store_ps(output+12, result3);
}

このコードは参考のために示したものです。

__m128 _mm_load_ps(float * p );

この組込み関数は、アドレス p から 4 つの連続する単精度浮動小数点データを 1 つの __m128 データにロードします (アドレス p は 16 バイトでアライメントされている必要があります)。

r0 := p[0]
r1 := p[1]
r2 := p[2]
r3 := p[3]

その他の最適化テクノロジー

ゲーム・コーディングに適用できる最適化テクノロジーやツールはほかにもあります。その 1 つは、ゲームコードの NDK 部分をコンパイルできる「インテル® C++ コンパイラー Android* 向け」です。このコンパイラーは、パイプライン、キャッシュ、メモリーの使用効率など、インテル® プロセッサー・アーキテクチャー向けの特別な最適化を行います。gcc* を使用してコードをコンパイルする場合は、パフォーマンスのチューニングと、キャッシュおよびメモリー使用率の向上のために、次のコンパイルオプションを指定する必要があります。

gcc* の最適化コンパイルオプション
LOCAL_CFLAGS := -O3 -ffast-math -mtune=atom -msse3 -mfpmath=sse

インテル® C++ コンパイラー Android* 向けの最適化コンパイルオプション
LOCAL_CFLAGS := -O3 -xSSSE3_atom -ipo -no-prec-div

インテル® VTune™ Amplifier 2011 for Android は、開発者がプログラムの hotspot (最も時間を費やしている部分) を迅速に特定し、キャッシュとメモリー使用量を確認してパフォーマンスと品質を向上できるように支援します。また、別の強力なツールであるインテル® グラフィックス・パフォーマンス・アナライザー (インテル® GPA) は、プロセッサー、GPU、メモリー、IO、グラフィック API など、システム全体の情報からソフトウェア実行のリアルタイム・ステータスをモニターして、ボトルネックを検出します。インテル® GPA はゲーム開発に最適です。


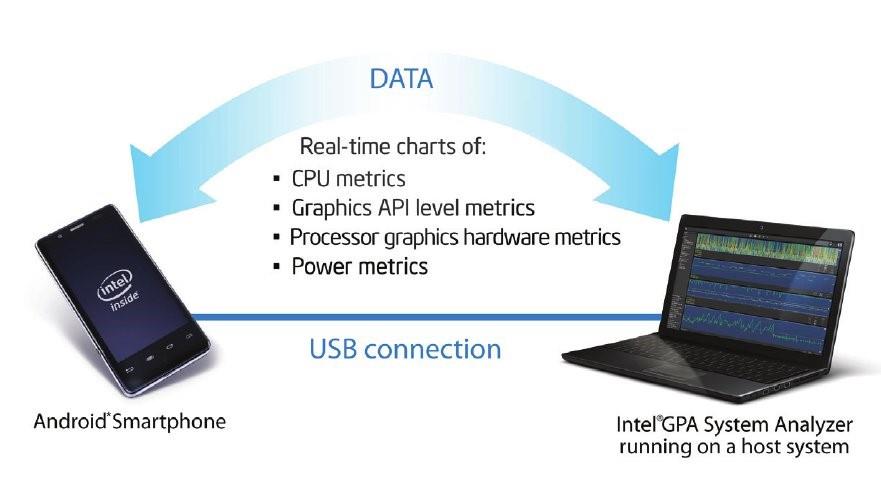
図 9. インテル® グラフィックス・パフォーマンス・アナライザー (インテル® GPA)

まとめ

インテル® SSE とインテル® C++ コンパイラー Android* 向けを用いてコンパイルし、インテル® GPA を利用することで、The Last Defender のパフォーマンスを大幅に向上させることができました。以前と同じテストシナリオで測定したところ、FPS は 30 から 39 に、約 30% 向上しました2。


図 10. 「The Last Defender」の非最適化バージョンのスナップショット (FPS はゲーム設定でオンにできます)


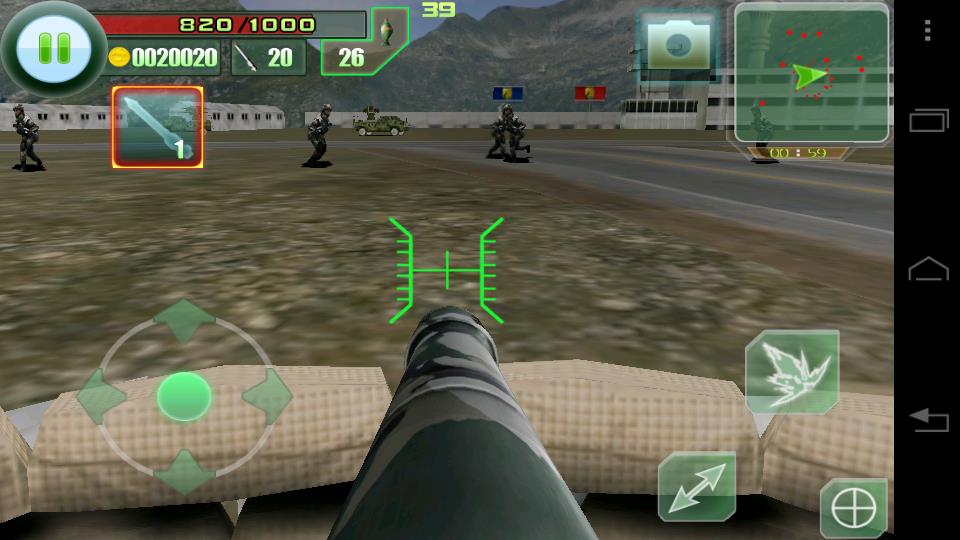
図 11. 「The Last Defender」の最適化バージョンのスナップショット (FPS はゲーム設定でオンにできます)

インテル® SSE テクノロジーによりゲームコードを高速化することはやりがいがあるものですが、難しい挑戦でもあります。この記事では、ゲームコードの高速化について簡単に説明しました。この記事をお読みになった Android* ゲーム開発者の皆さんが、IA の機能を活用してゲームコードを最適化し、より高速なゲームプレイと優れたユーザー体験を提供できることを願っています。

著者紹介

YANG Yi
インテル コーポレーションのソフトウェア・アプリケーション・エンジニア。現在、中国で、IA における Android* 向けゲームエンジンおよびグラフィックスの開発を支援するプロジェクトに取り組んでいます。多くの先進的なインテル® テクノロジーを利用して、中国のゲーム ISV がインテル® x86 Android* プラットフォームでハイパフォーマンスかつ高品質のゲームエンジン、そして人気があるゲームタイトルを開発できるように支援しています。

関連記事および関連情報

概要: インテル® ストリーミング SIMD 拡張命令 2 (インテル® SSE2) (https://software.intel.com/en-us/node/583138 (英語))
#pragma SIMD を使用してループをベクトル化するための条件
ストリーミング SIMD 拡張命令によるパーティクル・システムの作成 (http://software.intel.com/en-us/articles/creating-a-particle-system-with-streaming-simd-extensions)

Intel、インテル、Intel ロゴ、Intel Atom、VTune は、アメリカ合衆国および / またはその他の国における Intel Corporation の商標です。
© 2013 Intel Corporation. 無断での引用、転載を禁じます。
* その他の社名、製品名などは、一般に各社の表示、商標または登録商標です。

1 性能に関するテストに使用されるソフトウェアとワークロードは、性能がインテル® マイクロプロセッサー用に最適化されていることがあります。SYSmark* や MobileMark* などの性能テストは、特定のコンピューター・システム、コンポーネント、ソフトウェア、操作、機能に基づいて行ったものです。結果はこれらの要因によって異なります。製品の購入を検討される場合は、他の製品と組み合わせた場合の本製品の性能など、ほかの情報や性能テストも参考にして、パフォーマンスを総合的に評価することをお勧めします。
詳細については、http://www.intel.com/performance (英語) を参照してください。

2 性能に関するテストに使用されるソフトウェアとワークロードは、性能がインテル® マイクロプロセッサー用に最適化されていることがあります。SYSmark* や MobileMark* などの性能テストは、特定のコンピューター・システム、コンポーネント、ソフトウェア、操作、機能に基づいて行ったものです。結果はこれらの要因によって異なります。製品の購入を検討される場合は、他の製品と組み合わせた場合の本製品の性能など、ほかの情報や性能テストも参考にして、パフォーマンスを総合的に評価することをお勧めします。
詳細については、http://www.intel.com/performance (英語) を参照してください。

コンパイラーの最適化に関する詳細は、最適化に関する注意事項を参照してください。

タイトルとURLをコピーしました