この記事は、インテル® ソフトウェア・ネットワークに掲載されている「Predicting and Measuring Parallel Performance」(http://software.intel.com/en-us/articles/predicting-and-measuring-parallel-performance/) の日本語参考訳です。
編集注記:
本記事は、2011 年 5 月 4 日に公開されたものを、加筆・修正したものです。
はじめに
ソフトウェアを並列化すると、データセットを処理する時間の短縮、一定時間に処理できるデータセット数の増加、そしてスレッド化されていないソフトウェアでは扱うことが困難な大規模なデータセットの処理、などが可能になります。並列化が成功したかどうかは、通常、シリアルバージョンに対する並列バージョンのスピードアップを測定して判断します。また、得られたスピードアップの値を期待値の上限と比較することも大切です。スピードアップの期待値は、アムダールの法則とグスタフソンの法則を使用して求めることができます。
この記事は、「マルチスレッド・アプリケーションの開発のためのガイド」の一部で、インテル® プラットフォーム向けにマルチスレッド・アプリケーションを効率的に開発するための手法について説明します。
背景
アプリケーションの実行が高速化されるとユーザーの待機時間が短縮されます。また、実行時間が短縮されると、同じ時間でより大きなデータセット (より多くのデータレコード、より多くのピクセル、より大規模な物理モデル) を処理できるようになります。シリアル実行の時間と並列実行の時間を比較する指標としてよく用いられるのが、「スピードアップ」です。
スピードアップとは、簡単にいえば、シリアル実行にかかる時間と並列実行にかかる時間の比率のことです。例えば、シリアルバージョンでは実行に 6720 秒かかったアプリケーションが、(64 スレッドおよびコアを使用した) 並列バージョンでは 126.7 秒で実行できた場合、並列化によるスピードアップは約 53 倍 (6720/126.7 = 53.038) になります。
適切にスケーリングされたアプリケーションでは、スピードアップの値は増加したコア (スレッド) 数と同じまたは非常に近い値になります。使用するスレッド数を増やしてもスピードアップ値が増加しない、あるいは低下する場合、アプリケーションは測定に使用したデータセット用に適切にスケーリングされていません。そのデータセットがアプリケーションの典型的なデータセットの場合、アプリケーション自体のスケーラビリティーが低いといえます。
スピードアップに関連する指標として、「効率」があります。「スピードアップ」はシリアル実行に対して並列実行がどの程度高速化したかを判断する指標であるのに対して、「効率」はソフトウェアがシステムの計算リソースをどの程度活用しているかを示します。並列実行の効率を計算するには、スピードアップを使用したコア数で割り、その数値をパーセントで表します。例えば、64 コアでスピードアップが 53 倍だった場合、効率は 82.8% (53/64 = 0.828) です。つまり、実行中に各コアのアイドル時間が平均で約 17% あることになります。
アムダールの法則
並列化プロジェクトに取り組む前に、まず実現可能な性能向上 (スピードアップ) の値を予測します。並列に実行できるシリアルコードの比率が分かっていれば (または予測できれば)、アムダールの法則を使用することで、並列領域のコードを実際に記述することなく、アプリケーションのスピードアップの上限を計算できます。アムダールの法則の式には、いくつかのバリエーションがあります。どの式でも、並列実行時間の割合 (pctPar)、シリアル実行時間 (1 – pctPar)、スレッド数もしくはコア数 (p) が使用されます。p コアで実行した場合の並列アプリケーションのスピードアップを予測する単純なアムダールの法則の式を次に示します。
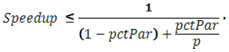
シリアル実行時間を 1 とし、シリアル時間の割合を使用して、予測される並列実行時間で割ります。並列実行時間は、シリアル実行時間 (1 – pctPar) と、並列実行時間の割合を使用するコア数で割った数 (pctPar/p) から予測できます。例えば、シリアル・アプリケーションの実行時間の 95% を 8 コアで並列実行可能な場合、アムダールの法則によるスピードアップの予測はほぼ 6 倍 (1 / (0.05 + 0.95/8) = 5.925) になります。
アムダールの法則の式では、並列に実行できる計算は、無限のコアに分割できると仮定しています。この仮定により、コア数が無限の場合、分母の第 2 項を (ゼロと見なして) 削除できるため、スピードアップの上限はシリアル実行の割合の逆数となります。
アムダールの法則は、無限のコア数を仮定していることに加えて、通信、同期、その他のスレッド管理などのオーバーヘッドを無視しているという批判を受けてきました。さらに、最も批判を受けているのは、コア数の増加に伴って処理するデータ量の増加を考慮していない点です。アムダールの法則では、使用するコア数に関係なくデータセットのサイズは固定であり、シリアル実行時間全体における割合は同じであると仮定されています。
グスタフソンの法則
8 個のコアを使用する並列アプリケーションが元のサイズの 8 倍のデータセットを計算できる場合、シリアル部分の実行時間は増加するでしょうか。もし増加する場合でも、データセットと同じ比率では増加しません。実際のデータでは、シリアル実行時間はほとんど一定です。
グスタフソンの法則は、コア数の増加に比例したデータサイズの増加を考慮に入れ、大規模なデータセットをシリアル実行できるものとして、アプリケーションのスピードアップ (の上限) を計算することで、スピードアップがスケールすることを示しました。スピードアップのスケールの式は以下のように表されます。
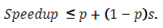
アムダールの法則の式と同様に、p はコア数です。表記をシンプルにするため、指定したデータセットにおける並列アプリケーションのシリアル実行時間の割合を s とします。例えば、32 コアの実行時間の 1% がシリアル実行に費やされる場合、同じデータセットをシングルスレッド、シングルコアで実行 (できると仮定) すると、アプリケーションのスピードアップは以下のようになります。
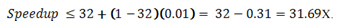
これらの仮定のもとで、アムダールの法則ではスピードアップがどのように予測されるか考えてみましょう。シリアル実行の割合を 1% と仮定すると、アムダールの法則の式では、スピードアップは 1/(0.01 + (0.99/32)) = 24.43 倍になります。しかし、シリアル実行の割合は 32 コアで実行した値であるため、この計算は誤りです。この例では、コア数が多い場合や少ない場合 (あるいは 1 コアの場合) のシリアル実行の割合が示されていません。コードが完全にスケーラブルでデータサイズがコア数とともにスケールするのであれば、この割合は一定となるため、32 コアでの (固定サイズの) シングルコア問題のスピードアップをアムダールの法則で予測できます。
一方、32 コアでの並列アプリケーションの合計実行時間が分かっている場合、シリアル実行時間を計算して、(さらに問題をシングルコアで計算できると仮定することで) 32 コアでの固定サイズ問題のスピードアップをアムダールの法則で予測できます。並列アプリケーションの合計実行時間が 1040 秒で、その 1% (10.4 秒) がシリアル実行時間であると仮定します。合計実行時間からシリアル実行時間を引いた値 (1029.6 秒) にコア数 (32) をかけて、シリアル実行時間 (10.4 秒) を加えた値、1029.6*32+10.4 = 32957.6 秒がアプリケーションの延べ実行時間になります。並列実行できない時間 (10.4 秒) は延べ実行時間の 0.032% です。この新しい値を使用すると、アムダールの法則によるスピードアップは 1/(0.00032 + (0.99968/32)) = 31.686 倍になります。
グスタフソンの法則では並列実行領域内のシリアル時間の割合が必要になるため、この式は通常、同じサイズの問題のシリアル実行に対する、(コア数の増加に伴ってデータセットが大きくなる) 並列実行のスピードアップの計算に使用されます。上記の例から、アムダールの法則の式にアプリケーション実行のデータを厳格に適用すると、グスタフソンの法則の式よりもかなり低い値になることが分かります。
推奨事項
スピードアップを計算するときは、最良のシリアル・アルゴリズムと最速のシリアルコードを比較する必要があります。最適でないシリアル・アルゴリズムのほうが並列化を容易に行える場合もありますが、より速いシリアルコードがすでに存在するのに遅いシリアルコードをあえて使用する人はまずいないでしょう。したがって、根本的なアルゴリズムが異なっても、最速のシリアルコードから得られる最良のシリアル実行時間を使用して、比較可能な並列アプリケーションのスピードアップを計算する必要があります。
スピードアップの値は、倍数で表します。以前は % で表されていたこともありますが、% 表現は混乱を招くために変更されました。例えば、並列コードがシリアルコードよりも 200% 高速であると表された場合、並列コードはシリアルバージョンの半分の時間で実行されるのでしょうか。それとも 3 分の 1 の時間で実行されるのでしょうか。105% のスピードアップと表された場合、シリアル実行とほぼ同じ時間で実行されるのでしょうか。それとも 2 倍の速度で実行されるのでしょうか。基準となるシリアル時間は 0% のスピードアップでしょうか。それとも 100% のスピードアップでしょうか。一方、並列アプリケーションが 2 倍にスピードアップした、と表された場合、半分の時間で実行できるようになった (つまり、シリアルコードを 1 回実行する時間で並列バージョンは 2 回実行できる) ことは明らかです。
非常に稀なケースですが、アプリケーションのスピードアップがコア数を上回ることがあります。この現象は、「スーパーリニア・スピードアップ」と呼ばれます。スーパーリニア・スピードアップの典型的な要因は、固定サイズのデータセットの分解により、コアあたりのデータが小さくなり、データがすべてローカルキャッシュに収まるようになることです。シリアル実行では、データはキャッシュに収まらないため、キャッシュラインがフェッチされる間、プロセッサーは待機します。データが大きいために以前使用したキャッシュラインが排出 (evict) された場合、それらを再利用するとプロセッサーは再度待機する必要があります。データがコア上のキャッシュにすべて収まるようなサイズに分割された場合、一旦キャッシュに配置された後は、キャッシュラインを再利用するときに待機する必要がありません。このように、複数のコアを使用すると、シングルコアで実行するシリアルコードに関連したオーバーヘッドを軽減できます。データセットが (典型的なデータセットよりも) 非常に小さいときにパフォーマンスが向上したと錯覚しないように注意する必要があります。
利用ガイドライン
アムダールの法則の単純なモデルにおける矛盾について合理的な仮定を試みる、さまざまな並列実行モデルが提案されてきました。
非常に簡潔で、(達成されるあるいは上回る可能性が非常に低い) 理論的なスピードアップの上限であると今でも広く見なされているアムダールの法則は、シリアル・アプリケーションのスピードアップの期待値を表す単純かつ貴重な指標であるといえるでしょう。


